|
GAUSS (software)
GAUSS is a matrix programming language for mathematics and statistics, developed and marketed by Aptech Systems. Its primary purpose is the solution of numerical problems in statistics, econometrics, time-series, optimization and 2D- and 3D- visualization. It was first published in 1984 for MS-DOS and is available for Linux, macOS and Windows. Examples * GAUSS has several Application Modules as well as functions in its Run-Time Library (i.e., functions that come with GAUSS without extra cost) ** Qprog – Quadratic programming ** SqpSolvemt – Sequential quadratic programming ** QNewton - Quasi-Newton unconstrained optimization ** EQsolve - Nonlinear equations solver GAUSS Applications A range of toolboxes are available for GAUSS at additional cost. See also * List of numerical-analysis software Listed here are notable end-user computer applications intended for use with numerical or data analysis: Numerical-software packages * Analytica is a widely used proprie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Aptech Systems
Aptech Limited is an Indian vocational training services provider headquartered Mumbai. Notable achievements * Media and Entertainment Skills Council (MESC) in association with Aptech Ltd’s two major brands Arena Animation and MAAC (Maya Academy of Advanced Cinematics) organised India’s First and largest media job festival. References {{reflist Further reading AI and automation to create more jobs opportunities for IT sectorHow professionals are using e-learning to be relevant at workplace? Software companies of India Software companies based in Mumbai Education companies established in 1986 Indian companies established in 1986 1986 establishments in Maharashtra Companies listed on the Bombay Stock Exchange Companies listed on the National Stock Exchange of India ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
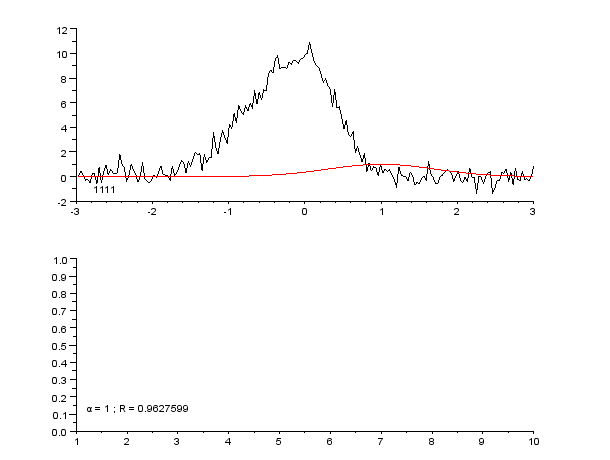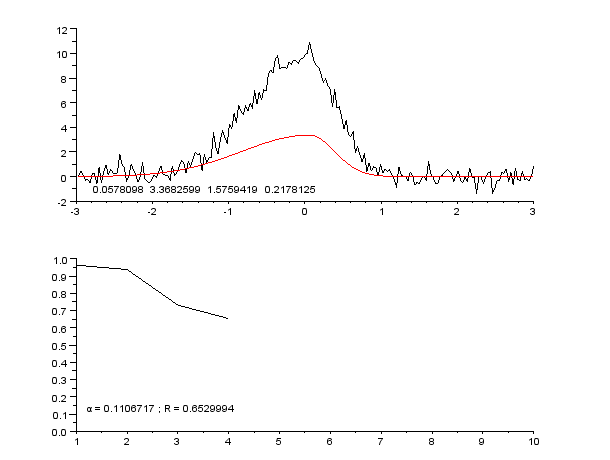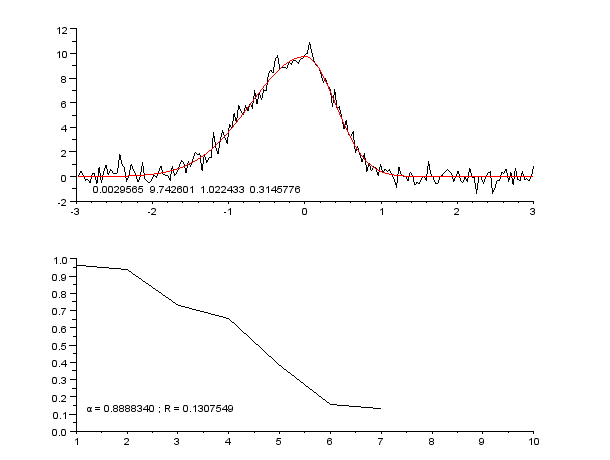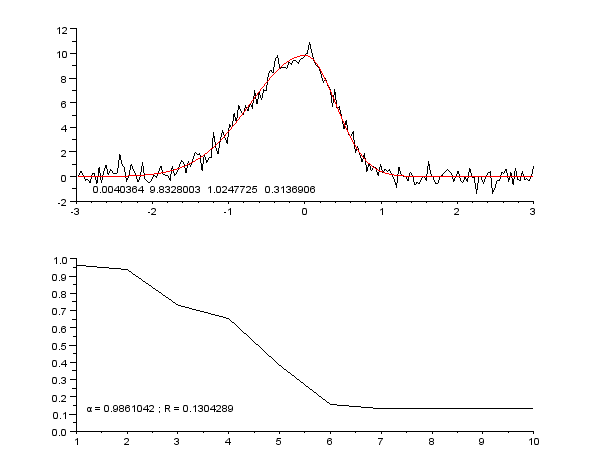
Curve Fitting
Curve fitting is the process of constructing a curve, or mathematical function, that has the best fit to a series of data points, possibly subject to constraints. Curve fitting can involve either interpolation, where an exact fit to the data is required, or smoothing, in which a "smooth" function is constructed that approximately fits the data. A related topic is regression analysis, which focuses more on questions of statistical inference such as how much uncertainty is present in a curve that is fitted to data observed with random errors. Fitted curves can be used as an aid for data visualization, to infer values of a function where no data are available, and to summarize the relationships among two or more variables. Extrapolation refers to the use of a fitted curve beyond the range of the observed data, and is subject to a degree of uncertainty since it may reflect the method used to construct the curve as much as it reflects the observed data. For linear-algebraic ana ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cointegration
In econometrics, cointegration is a statistical property describing a long-term, stable relationship between two or more time series variables, even if those variables themselves are individually non-stationary (i.e., they have trends). This means that despite their individual fluctuations, the variables move together in the long run, anchored by an underlying equilibrium relationship. More formally, if several time series are individually integrated of order ''d'' (meaning they require ''d'' differences to become stationary) but a linear combination of them is integrated of a lower order, then those time series are said to be cointegrated. That is, if (''X'',''Y'',''Z'') are each integrated of order ''d'', and there exist coefficients ''a'',''b'',''c'' such that is integrated of order less than d, then ''X'', ''Y'', and ''Z'' are cointegrated. Cointegration is a crucial concept in time series analysis, particularly when dealing with variables that exhibit trends, such as ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Panel Data
In statistics and econometrics, panel data and longitudinal data are both multi-dimensional data involving measurements over time. Panel data is a subset of longitudinal data where observations are for the same subjects each time. Time series and cross-sectional data can be thought of as special cases of panel data that are in one dimension only (one panel member or individual for the former, one time point for the latter). A literature search often involves time series, cross-sectional, or panel data. A study that uses panel data is called a longitudinal study or panel study. Example In the multiple response permutation procedure (MRPP) example above, two datasets with a panel structure are shown and the objective is to test whether there's a significant difference between people in the sample data. Individual characteristics (income, age, sex) are collected for different persons and different years. In the first dataset, two persons (1, 2) are observed every year for three ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Error Correction Model
An error correction model (ECM) belongs to a category of multiple time series models most commonly used for data where the underlying variables have a long-run common stochastic trend, also known as cointegration. ECMs are a theoretically-driven approach useful for estimating both short-term and long-term effects of one time series on another. The term error-correction relates to the fact that last-period's deviation from a long-run equilibrium, the ''error'', influences its short-run dynamics. Thus ECMs directly estimate the speed at which a dependent variable returns to equilibrium after a change in other variables. History Yule (1926) and Granger and Newbold (1974) were the first to draw attention to the problem of spurious correlation and find solutions on how to address it in time series analysis. Given two completely unrelated but integrated (non-stationary) time series, the regression analysis of one on the other will tend to produce an apparently statistically significa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Autoregressive Integrated Moving Average
In time series analysis used in statistics and econometrics, autoregressive integrated moving average (ARIMA) and seasonal ARIMA (SARIMA) models are generalizations of the autoregressive moving average (ARMA) model to non-stationary series and periodic variation, respectively. All these models are fitted to time series in order to better understand it and predict future values. The purpose of these generalizations is to fit the data as well as possible. Specifically, ARMA assumes that the series is stationary, that is, its expected value is constant in time. If instead the series has a trend (but a constant variance/ autocovariance), the trend is removed by "differencing", leaving a stationary series. This operation generalizes ARMA and corresponds to the " integrated" part of ARIMA. Analogously, periodic variation is removed by "seasonal differencing". Components As in ARMA, the "autoregressive" () part of ARIMA indicates that the evolving variable of interest is regressed on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
System Of Polynomial Equations
A system of polynomial equations (sometimes simply a polynomial system) is a set of simultaneous equations where the are polynomials in several variables, say , over some Field (mathematics), field . A ''solution'' of a polynomial system is a set of values for the s which belong to some algebraically closed field extension of , and make all equations true. When is the field of rational numbers, is generally assumed to be the field of complex numbers, because each solution belongs to a field extension of , which is isomorphic to a subfield of the complex numbers. This article is about the methods for solving, that is, finding all solutions or describing them. As these methods are designed for being implemented in a computer, emphasis is given on fields in which computation (including equality testing) is easy and efficient, that is the field of rational numbers and finite fields. Searching for solutions that belong to a specific set is a problem which is generally much more d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Maximum Likelihood Estimation
In statistics, maximum likelihood estimation (MLE) is a method of estimation theory, estimating the Statistical parameter, parameters of an assumed probability distribution, given some observed data. This is achieved by Mathematical optimization, maximizing a likelihood function so that, under the assumed statistical model, the Realization (probability), observed data is most probable. The point estimate, point in the parameter space that maximizes the likelihood function is called the maximum likelihood estimate. The logic of maximum likelihood is both intuitive and flexible, and as such the method has become a dominant means of statistical inference. If the likelihood function is Differentiable function, differentiable, the derivative test for finding maxima can be applied. In some cases, the first-order conditions of the likelihood function can be solved analytically; for instance, the ordinary least squares estimator for a linear regression model maximizes the likelihood when ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Log-linear Analysis
Log-linear analysis is a technique used in statistics to examine the relationship between more than two categorical variables. The technique is used for both hypothesis testing and model building. In both these uses, models are tested to find the most parsimonious (i.e., least complex) model that best accounts for the variance in the observed frequencies. (A Pearson's chi-square test could be used instead of log-linear analysis, but that technique only allows for two of the variables to be compared at a time.) Fitting criterion Log-linear analysis uses a likelihood ratio statistic \Chi^2 that has an approximate chi-square distribution when the sample size is large: :\Chi^2 = 2\sum O_ \ln \frac, where :\ln = natural logarithm; :O_ = observed frequency in cell''ij'' (''i'' = row and ''j'' = column); :E_ = expected frequency in cell''ij''. :\Chi^2 = the deviance for the model. Assumptions There are three assumptions in log-linear analysis: 1. The observations are independe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Categorical Variable
In statistics, a categorical variable (also called qualitative variable) is a variable that can take on one of a limited, and usually fixed, number of possible values, assigning each individual or other unit of observation to a particular group or nominal category on the basis of some qualitative property. In computer science and some branches of mathematics, categorical variables are referred to as enumerations or enumerated types. Commonly (though not in this article), each of the possible values of a categorical variable is referred to as a level. The probability distribution associated with a random categorical variable is called a categorical distribution. Categorical data is the statistical data type consisting of categorical variables or of data that has been converted into that form, for example as grouped data. More specifically, categorical data may derive from observations made of qualitative data that are summarised as counts or cross tabulations, or from observat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Least Squares
The method of least squares is a mathematical optimization technique that aims to determine the best fit function by minimizing the sum of the squares of the differences between the observed values and the predicted values of the model. The method is widely used in areas such as regression analysis, curve fitting and data modeling. The least squares method can be categorized into linear and nonlinear forms, depending on the relationship between the model parameters and the observed data. The method was first proposed by Adrien-Marie Legendre in 1805 and further developed by Carl Friedrich Gauss. History Founding The method of least squares grew out of the fields of astronomy and geodesy, as scientists and mathematicians sought to provide solutions to the challenges of navigating the Earth's oceans during the Age of Discovery. The accurate description of the behavior of celestial bodies was the key to enabling ships to sail in open seas, where sailors could no longer rely on la ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Programming
Linear programming (LP), also called linear optimization, is a method to achieve the best outcome (such as maximum profit or lowest cost) in a mathematical model whose requirements and objective are represented by linear function#As a polynomial function, linear relationships. Linear programming is a special case of mathematical programming (also known as mathematical optimization). More formally, linear programming is a technique for the mathematical optimization, optimization of a linear objective function, subject to linear equality and linear inequality Constraint (mathematics), constraints. Its feasible region is a convex polytope, which is a set defined as the intersection (mathematics), intersection of finitely many Half-space (geometry), half spaces, each of which is defined by a linear inequality. Its objective function is a real number, real-valued affine function, affine (linear) function defined on this polytope. A linear programming algorithm finds a point in the po ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |