|
Fokker–Planck Equation
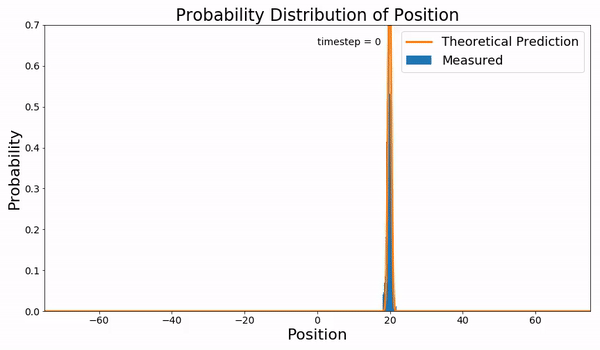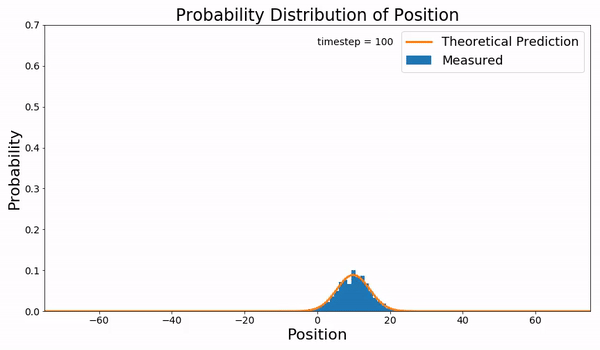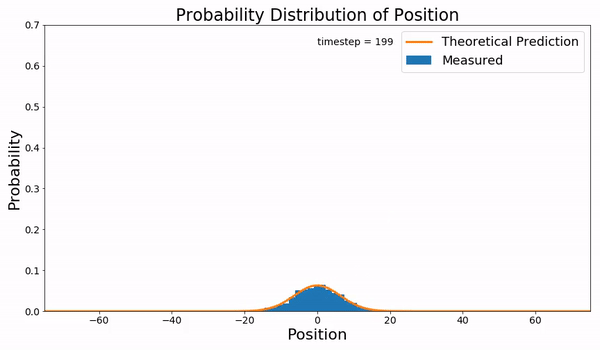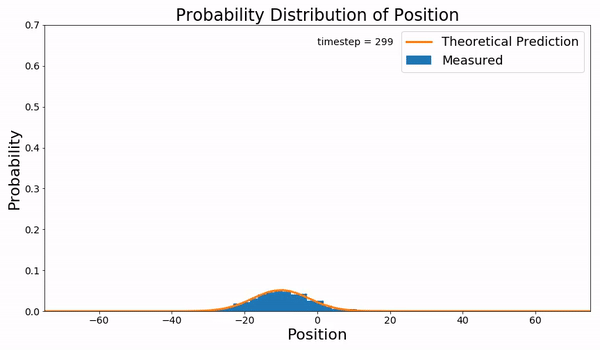
In statistical mechanics, the Fokker–Planck equation is a partial differential equation that describes the time evolution of the probability density function of the velocity of a particle under the influence of drag forces and random forces, as in Brownian motion. The equation can be generalized to other observables as well. It is named after Adriaan Fokker and Max Planck, who described it in 1914 and 1917. It is also known as the Kolmogorov forward equation, after Andrey Kolmogorov, who independently discovered it in 1931. When applied to particle position distributions, it is better known as the Smoluchowski equation (after Marian Smoluchowski), and in this context it is equivalent to the convection–diffusion equation. The case with zero diffusion is the continuity equation. The Fokker–Planck equation is obtained from the master equation through Kramers–Moyal expansion. The first consistent microscopic derivation of the Fokker–Planck equation in the single schem ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kramers–Moyal Expansion
In stochastic processes, Kramers–Moyal expansion refers to a Taylor series expansion of the master equation, named after Hans Kramers and José Enrique Moyal. This expansion transforms the integro-differential master equation :\frac =\int dx' x')p(x',t)-W(x', x)p(x,t)/math> where p(x,t, x_0,t_0) (for brevity, this probability is denoted by p(x,t)) is the transition probability density, to an infinite order partial differential equation :\frac = \sum_^\infty \frac \frac alpha_n(x) p(x,t)/math> where :\alpha_n(x) = \int_^\infty (x'-x)^n W(x'\mid x) \ dx'. Here W(x'\mid x) is the transition probability rate. The Fokker–Planck equation is obtained by keeping only the first two terms of the series in which \alpha_1 is the drift Drift or Drifts may refer to: Geography * Drift or ford (crossing) of a river * Drift, Kentucky, unincorporated community in the United States * In Cornwall, England: ** Drift, Cornwall, village ** Drift Reservoir, associated with the village ... ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stratonovich Integral
In stochastic processes, the Stratonovich integral (developed simultaneously by Ruslan Stratonovich and Donald Fisk) is a stochastic integral, the most common alternative to the Itô integral. Although the Itô integral is the usual choice in applied mathematics, the Stratonovich integral is frequently used in physics. In some circumstances, integrals in the Stratonovich definition are easier to manipulate. Unlike the Itô calculus, Stratonovich integrals are defined such that the chain rule of ordinary calculus holds. Perhaps the most common situation in which these are encountered is as the solution to Stratonovich stochastic differential equations (SDEs). These are equivalent to Itô SDEs and it is possible to convert between the two whenever one definition is more convenient. Definition The Stratonovich integral can be defined in a manner similar to the Riemann integral, that is as a limit of Riemann sums. Suppose that W : , T\times \Omega \to \mathbb is a Wiener process ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Feynman–Kac Formula
The Feynman–Kac formula, named after Richard Feynman and Mark Kac, establishes a link between parabolic partial differential equations (PDEs) and stochastic processes. In 1947, when Kac and Feynman were both Cornell faculty, Kac attended a presentation of Feynman's and remarked that the two of them were working on the same thing from different directions. The Feynman–Kac formula resulted, which proves rigorously the real case of Feynman's path integrals. The complex case, which occurs when a particle's spin is included, is still unproven. It offers a method of solving certain partial differential equations by simulating random paths of a stochastic process. Conversely, an important class of expectations of random processes can be computed by deterministic methods. Theorem Consider the partial differential equation :\frac(x,t) + \mu(x,t) \frac(x,t) + \tfrac \sigma^2(x,t) \frac(x,t) -V(x,t) u(x,t) + f(x,t) = 0, defined for all x \in \mathbb and t \in , T/math>, subject to th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Itô's Lemma
In mathematics, Itô's lemma or Itô's formula (also called the Itô-Doeblin formula, especially in French literature) is an identity used in Itô calculus to find the differential of a time-dependent function of a stochastic process. It serves as the stochastic calculus counterpart of the chain rule. It can be heuristically derived by forming the Taylor series expansion of the function up to its second derivatives and retaining terms up to first order in the time increment and second order in the Wiener process increment. The lemma is widely employed in mathematical finance, and its best known application is in the derivation of the Black–Scholes equation for option values. Motivation Suppose we are given the stochastic differential equation dX_t = \mu_t\ dt + \sigma_t\ dB_t, where is a Wiener process and the functions \mu_t, \sigma_t are deterministic (not stochastic) functions of time. In general, it's not possible to write a solution X_t directly in terms of B_t. Howeve ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Infinitesimal Generator (stochastic Processes)
In mathematics — specifically, in stochastic analysis — the infinitesimal generator of a Feller process (i.e. a continuous-time Markov process satisfying certain regularity conditions) is a Fourier multiplier operator that encodes a great deal of information about the process. The generator is used in evolution equations such as the Kolmogorov backward equation (which describes the evolution of statistics of the process); its ''L''2 Hermitian adjoint is used in evolution equations such as the Fokker–Planck equation (which describes the evolution of the probability density functions of the process). Definition General case For a Feller process (X_t)_ with Feller semigroup T=(T_t)_ and state space E we define the generator (A,D(A)) by :D(A)=\left\, :A f=\lim_ \frac, for any f\in D(A). Here C_(E) denotes the Banach space of continuous functions on E vanishing at infinity, equipped with the supremum norm, and T_t f(x)= \mathbb^x f(X_t)=\mathbb(f(X_t), X_0=x). In ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Drift Velocity
In physics, a drift velocity is the average velocity attained by charged particles, such as electrons, in a material due to an electric field. In general, an electron in a conductor will propagate randomly at the Fermi velocity, resulting in an average velocity of zero. Applying an electric field adds to this random motion a small net flow in one direction; this is the drift. Drift velocity is proportional to current. In a resistive material, it is also proportional to the magnitude of an external electric field. Thus Ohm's law can be explained in terms of drift velocity. The law's most elementary expression is: : u= \mu E , where is drift velocity, is the material's electron mobility, and is the electric field. In the MKS system, these quantities' units are m/s, m2/( V·s), and V/m, respectively. When a potential difference is applied across a conductor, free electrons gain velocity in the direction, opposite to the electric field between successive collisions (and lose ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stochastic Differential Equation
A stochastic differential equation (SDE) is a differential equation in which one or more of the terms is a stochastic process, resulting in a solution which is also a stochastic process. SDEs are used to model various phenomena such as stock prices or physical systems subject to thermal fluctuations. Typically, SDEs contain a variable which represents random white noise calculated as the derivative of Brownian motion or the Wiener process. However, other types of random behaviour are possible, such as jump processes. Random differential equations are conjugate to stochastic differential equations. Background Stochastic differential equations originated in the theory of Brownian motion, in the work of Albert Einstein and Smoluchowski. These early examples were linear stochastic differential equations, also called 'Langevin' equations after French physicist Langevin, describing the motion of a harmonic oscillator subject to a random force. The mathematical theory of stochasti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wiener Process
In mathematics, the Wiener process is a real-valued continuous-time stochastic process named in honor of American mathematician Norbert Wiener for his investigations on the mathematical properties of the one-dimensional Brownian motion. It is often also called Brownian motion due to its historical connection with the physical process of the same name originally observed by Scottish botanist Robert Brown (Scottish botanist from Montrose), Robert Brown. It is one of the best known Lévy processes (càdlàg stochastic processes with stationary increments, stationary independent increments) and occurs frequently in pure and applied mathematics, economy, economics, quantitative finance, evolutionary biology, and physics. The Wiener process plays an important role in both pure and applied mathematics. In pure mathematics, the Wiener process gave rise to the study of continuous time martingale (probability theory), martingales. It is a key process in terms of which more complicated sto ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Itô Calculus
Itô calculus, named after Kiyosi Itô, extends the methods of calculus to stochastic processes such as Brownian motion (see Wiener process). It has important applications in mathematical finance and stochastic differential equations. The central concept is the Itô stochastic integral, a stochastic generalization of the Riemann–Stieltjes integral in analysis. The integrands and the integrators are now stochastic processes: :Y_t=\int_0^t H_s\,dX_s, where ''H'' is a locally square-integrable process adapted to the filtration generated by ''X'' , which is a Brownian motion or, more generally, a semimartingale. The result of the integration is then another stochastic process. Concretely, the integral from 0 to any particular ''t'' is a random variable, defined as a limit of a certain sequence of random variables. The paths of Brownian motion fail to satisfy the requirements to be able to apply the standard techniques of calculus. So with the integrand a stochastic process, the Itô ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nikolay Mitrofanovich Krylov
Nikolay Mitrofanovich Krylov (russian: Никола́й Митрофа́нович Крыло́в, uk, Микола Митрофанович Крилов) ( – May 11, 1955) was a Russian and Soviet mathematician known for works on interpolation, non-linear mechanics, and numerical methods for solving equations of mathematical physics. Biography Nikolay Krylov graduated from St. Petersburg State Mining Institute in 1902. In the period from 1912 until 1917, he held the Professor position in this institute. In 1917, he went to the Crimea to become Professor at the Crimea University. He worked there until 1922 and then moved to Kyiv to become chairman of the mathematical physics department at the Ukrainian Academy of Sciences. Nikolay Krylov was a member of the Société Mathématique de France and the American Mathematical Society. Research Nikolay Krylov developed new methods for analysis of equations of mathematical physics, which can be used not only for proving the existence ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
