|
Flexural Modulus
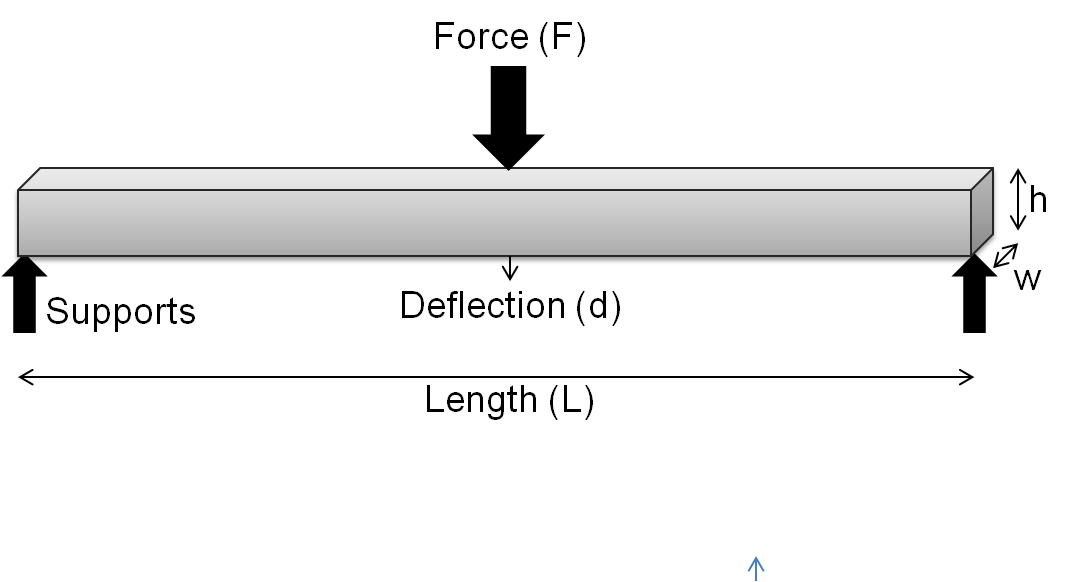
In mechanics, the flexural modulus or bending modulus is an intensive property that is computed as the ratio of stress to strain in flexural deformation, or the tendency for a material to resist bending. It is determined from the slope of a stress-strain curve produced by a flexural test (such as the ASTM D790), and uses units of force per area. The flexural modulus defined using the 2-point (cantilever) and 3-point bend tests assumes a linear stress strain response. For a 3-point test of a rectangular beam behaving as an isotropic linear material, where ''w'' and ''h'' are the width and height of the beam, ''I'' is the second moment of area of the beam's cross-section, ''L'' is the distance between the two outer supports, and ''d'' is the deflection due to the load ''F'' applied at the middle of the beam, the flexural modulus: : E_ = \frac From elastic beam theory :d = \frac and for rectangular beam : I = \fracwh^3 thus E_ = E (Elastic modulus) For very small strains ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mechanics
Mechanics (from Ancient Greek: μηχανική, ''mēkhanikḗ'', "of machines") is the area of mathematics and physics concerned with the relationships between force, matter, and motion among physical objects. Forces applied to objects result in displacements, or changes of an object's position relative to its environment. Theoretical expositions of this branch of physics has its origins in Ancient Greece, for instance, in the writings of Aristotle and Archimedes (see History of classical mechanics and Timeline of classical mechanics). During the early modern period, scientists such as Galileo, Kepler, Huygens, and Newton laid the foundation for what is now known as classical mechanics. As a branch of classical physics, mechanics deals with bodies that are either at rest or are moving with velocities significantly less than the speed of light. It can also be defined as the physical science that deals with the motion of and forces on bodies not in the quantum r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stress (physics)
In continuum mechanics, stress is a physical quantity. It is a quantity that describes the magnitude of forces that cause deformation. Stress is defined as ''force per unit area''. When an object is pulled apart by a force it will cause elongation which is also known as deformation, like the stretching of an elastic band, it is called tensile stress. But, when the forces result in the compression of an object, it is called compressive stress. It results when forces like tension or compression act on a body. The greater this force and the smaller the cross-sectional area of the body on which it acts, the greater the stress. Therefore, stress is measured in newton per square meter (N/m2) or pascal (Pa). Stress expresses the internal forces that neighbouring particles of a continuous material exert on each other, while strain is the measure of the deformation of the material. For example, when a solid vertical bar is supporting an overhead weight, each particle in the bar pushe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Strain (materials Science)
In physics, deformation is the continuum mechanics transformation of a body from a ''reference'' configuration to a ''current'' configuration. A configuration is a set containing the positions of all particles of the body. A deformation can occur because of external loads, intrinsic activity (e.g. muscle contraction), body forces (such as gravity or electromagnetic forces), or changes in temperature, moisture content, or chemical reactions, etc. Strain is related to deformation in terms of ''relative'' displacement of particles in the body that excludes rigid-body motions. Different equivalent choices may be made for the expression of a strain field depending on whether it is defined with respect to the initial or the final configuration of the body and on whether the metric tensor or its dual is considered. In a continuous body, a deformation field results from a stress field due to applied forces or because of some changes in the temperature field of the body. Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Flexural Strength
Flexural strength, also known as modulus of rupture, or bend strength, or transverse rupture strength is a material property, defined as the stress in a material just before it yields in a flexure test. The transverse bending test is most frequently employed, in which a specimen having either a circular or rectangular cross-section is bent until fracture or yielding using a three-point flexural test technique. The flexural strength represents the highest stress experienced within the material at its moment of yield. It is measured in terms of stress, here given the symbol \sigma. Introduction When an object is formed of a single material, like a wooden beam or a steel rod, is bent (Fig. 1), it experiences a range of stresses across its depth (Fig. 2). At the edge of the object on the inside of the bend (concave face) the stress will be at its maximum compressive stress value. At the outside of the bend (convex face) the stress will be at its maximum tensile value. These ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
ASTM
ASTM International, formerly known as American Society for Testing and Materials, is an international standards organization that develops and publishes voluntary consensus technical standards for a wide range of materials, products, systems, and services. Some 12,575 ASTM voluntary consensus standards operate globally. The organization's headquarters is in West Conshohocken, Pennsylvania, about northwest of Philadelphia. It is founded in 1902 as the American Section of the International Association for Testing Materials (see also International Organization for Standardization). History A group of scientists and engineers, led by Charles Dudley, formed ASTM in 1898 to address the frequent rail breaks affecting the fast-growing railroad industry. The group developed a standard for the steel used to fabricate rails. Originally called the "American Society for Testing Materials" in 1902, it became the "American Society for Testing And Materials" in 1961. In 2001, ASTM offic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Second Moment Of Area
The second moment of area, or second area moment, or quadratic moment of area and also known as the area moment of inertia, is a geometrical property of an area which reflects how its points are distributed with regard to an arbitrary axis. The second moment of area is typically denoted with either an I (for an axis that lies in the plane of the area) or with a J (for an axis perpendicular to the plane). In both cases, it is calculated with a multiple integral over the object in question. Its dimension is L (length) to the fourth power. Its unit of dimension, when working with the International System of Units, is meters to the fourth power, m4, or inches to the fourth power, in4, when working in the Imperial System of Units. In structural engineering, the second moment of area of a beam is an important property used in the calculation of the beam's deflection and the calculation of stress caused by a moment applied to the beam. In order to maximize the second moment of area ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elastic Modulus
An elastic modulus (also known as modulus of elasticity) is the unit of measurement of an object's or substance's resistance to being deformed elastically (i.e., non-permanently) when a stress is applied to it. The elastic modulus of an object is defined as the slope of its stress–strain curve in the elastic deformation region: A stiffer material will have a higher elastic modulus. An elastic modulus has the form: :\delta \ \stackrel\ \frac where stress is the force causing the deformation divided by the area to which the force is applied and strain is the ratio of the change in some parameter caused by the deformation to the original value of the parameter. Since strain is a dimensionless quantity, the units of \delta will be the same as the units of stress. Specifying how stress and strain are to be measured, including directions, allows for many types of elastic moduli to be defined. The three primary ones are: # ''Young's modulus'' (E) describes tensile and compressive ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isotropy
Isotropy is uniformity in all orientations; it is derived . Precise definitions depend on the subject area. Exceptions, or inequalities, are frequently indicated by the prefix ' or ', hence ''anisotropy''. ''Anisotropy'' is also used to describe situations where properties vary systematically, dependent on direction. Isotropic radiation has the same intensity regardless of the direction of measurement, and an isotropic field exerts the same action regardless of how the test particle is oriented. Mathematics Within mathematics, ''isotropy'' has a few different meanings: ; Isotropic manifolds: A manifold is isotropic if the geometry on the manifold is the same regardless of direction. A similar concept is homogeneity. ; Isotropic quadratic form: A quadratic form ''q'' is said to be isotropic if there is a non-zero vector ''v'' such that ; such a ''v'' is an isotropic vector or null vector. In complex geometry, a line through the origin in the direction of an isotropic vecto ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Modulus Of Elasticity
An elastic modulus (also known as modulus of elasticity) is the unit of measurement of an object's or substance's resistance to being deformed elastically (i.e., non-permanently) when a stress is applied to it. The elastic modulus of an object is defined as the slope of its stress–strain curve in the elastic deformation region: A stiffer material will have a higher elastic modulus. An elastic modulus has the form: :\delta \ \stackrel\ \frac where stress is the force causing the deformation divided by the area to which the force is applied and strain is the ratio of the change in some parameter caused by the deformation to the original value of the parameter. Since strain is a dimensionless quantity, the units of \delta will be the same as the units of stress. Specifying how stress and strain are to be measured, including directions, allows for many types of elastic moduli to be defined. The three primary ones are: # ''Young's modulus'' (E) describes tensile and compressiv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Young's Modulus
Young's modulus E, the Young modulus, or the modulus of elasticity in tension or compression (i.e., negative tension), is a mechanical property that measures the tensile or compressive stiffness of a solid material when the force is applied lengthwise. It quantifies the relationship between tensile/compressive stress \sigma (force per unit area) and axial strain \varepsilon (proportional deformation) in the linear elastic region of a material and is determined using the formula: E = \frac Young's moduli are typically so large that they are expressed not in pascals but in gigapascals (GPa). Example: * Silly Putty (increasing pressure: length increases quickly, meaning tiny E) * Aluminum (increasing pressure: length increases slowly, meaning high E) Higher Young's modulus corresponds to greater (lengthwise) stiffness. Although Young's modulus is named after the 19th-century British scientist Thomas Young, the concept was developed in 1727 by Leonhard Euler. The first exp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Composite Material
A composite material (also called a composition material or shortened to composite, which is the common name) is a material which is produced from two or more constituent materials. These constituent materials have notably dissimilar chemical or physical properties and are merged to create a material with properties unlike the individual elements. Within the finished structure, the individual elements remain separate and distinct, distinguishing composites from mixtures and solid solutions. Typical engineered composite materials include: * Reinforced concrete and masonry *Composite wood such as plywood * Reinforced plastics, such as fibre-reinforced polymer or fiberglass * Ceramic matrix composites ( composite ceramic and metal matrices) *Metal matrix composites *and other advanced composite materials There are various reasons where new material can be favoured. Typical examples include materials which are less expensive, lighter, stronger or more durable when compared with ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |