|
Fuzzy Number
A fuzzy number is a generalization of a regular real number in the sense that it does not refer to one single value but rather to a connected set of possible values, where each possible value has its own weight between 0 and 1. This weight is called the membership function. A fuzzy number is thus a special case of a convex, normalized fuzzy set of the real line. Just like fuzzy logic is an extension of Boolean logic (which uses absolute truth and falsehood only, and nothing in between), fuzzy numbers are an extension of real numbers. Calculations with fuzzy numbers allow the incorporation of uncertainty on parameters, properties, geometry, initial conditions, etc. The arithmetic calculations on fuzzy numbers are implemented using fuzzy arithmetic operations, which can be done by two different approaches: (1) interval arithmetic approach; and (2) the extension principle approach. A fuzzy number is equal to a fuzzy interval. The degree of fuzziness is determined by the a-cut whic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fuzzy Arithmetic
Fuzzy or Fuzzies may refer to: Music * Fuzzy (band), a 1990s Boston indie pop band * Fuzzy (composer) (born 1939), Danish composer Jens Vilhelm Pedersen * ''Fuzzy'' (album), 1993 debut album by the Los Angeles rock group Grant Lee Buffalo * "Fuzzy", a song from the 2009 '' Collective Soul'' album by Collective Soul * "Fuzzy", a song by Poppy from ''Poppy.Computer'' Nickname * Faustina Agolley (born 1984), Australian television presenter, host of the Australian television show ''Video Hits'' * Fuzzy Haskins (born 1941), American singer and guitarist with the doo-wop group Parliament-Funkadelic * Fuzzy Hufft (1901−1973), American baseball player * Fuzzy Knight (1901−1976), American actor * Andrew Levane (1920−2012), American National Basketball Association player and coach * Robert Alfred Theobald (1884−1957), United States Navy rear admiral * Fuzzy Thurston (1933-2014), American National Football League player * Fuzzy Vandivier (1903−1983), American high school and c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Real Number
In mathematics, a real number is a number that can be used to measure a ''continuous'' one-dimensional quantity such as a distance, duration or temperature. Here, ''continuous'' means that values can have arbitrarily small variations. Every real number can be almost uniquely represented by an infinite decimal expansion. The real numbers are fundamental in calculus (and more generally in all mathematics), in particular by their role in the classical definitions of limits, continuity and derivatives. The set of real numbers is denoted or \mathbb and is sometimes called "the reals". The adjective ''real'' in this context was introduced in the 17th century by René Descartes to distinguish real numbers, associated with physical reality, from imaginary numbers (such as the square roots of ), which seemed like a theoretical contrivance unrelated to physical reality. The real numbers include the rational numbers, such as the integer and the fraction . The rest of the real number ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
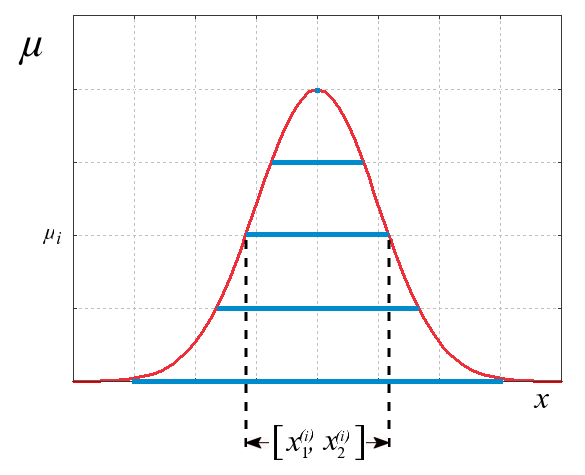
Membership Function (mathematics)
In mathematics, the membership function of a fuzzy set is a generalization of the indicator function for classical sets. In fuzzy logic, it represents the degree of truth as an extension of valuation. Degrees of truth are often confused with probabilities, although they are conceptually distinct, because fuzzy truth represents membership in vaguely defined sets, not likelihood of some event or condition. Membership functions were introduced by Aliasker Zadeh in the first paper on fuzzy sets (1965). Aliasker Zadeh, in his theory of fuzzy sets, proposed using a membership function (with a range covering the interval (0,1)) operating on the domain of all possible values. Definition For any set X, a membership function on X is any function from X to the real unit interval ,1/math>. Membership functions represent fuzzy subsets of X. The membership function which represents a fuzzy set \tilde A is usually denoted by \mu_A. For an element x of X, the value \mu_A(x) is called th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fuzzy Set
In mathematics, fuzzy sets (a.k.a. uncertain sets) are sets whose elements have degrees of membership. Fuzzy sets were introduced independently by Lotfi A. Zadeh in 1965 as an extension of the classical notion of set. At the same time, defined a more general kind of structure called an ''L''-relation, which he studied in an abstract algebraic context. Fuzzy relations, which are now used throughout fuzzy mathematics and have applications in areas such as linguistics , decision-making , and clustering , are special cases of ''L''-relations when ''L'' is the unit interval , 1 In classical set theory, the membership of elements in a set is assessed in binary terms according to a bivalent condition—an element either belongs or does not belong to the set. By contrast, fuzzy set theory permits the gradual assessment of the membership of elements in a set; this is described with the aid of a membership function valued in the real unit interval , 1 Fuzzy sets generali ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fuzzy Logic
Fuzzy logic is a form of many-valued logic in which the truth value of variables may be any real number between 0 and 1. It is employed to handle the concept of partial truth, where the truth value may range between completely true and completely false. By contrast, in Boolean logic, the truth values of variables may only be the integer values 0 or 1. The term ''fuzzy logic'' was introduced with the 1965 proposal of fuzzy set theory by Iranian Azerbaijani mathematician Lotfi Zadeh. Fuzzy logic had, however, been studied since the 1920s, as infinite-valued logic—notably by Łukasiewicz and Tarski. Fuzzy logic is based on the observation that people make decisions based on imprecise and non-numerical information. Fuzzy models or sets are mathematical means of representing vagueness and imprecise information (hence the term fuzzy). These models have the capability of recognising, representing, manipulating, interpreting, and using data and information that are vague and lack ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boolean Logic
In mathematics and mathematical logic, Boolean algebra is a branch of algebra. It differs from elementary algebra in two ways. First, the values of the variable (mathematics), variables are the truth values ''true'' and ''false'', usually denoted 1 and 0, whereas in elementary algebra the values of the variables are numbers. Second, Boolean algebra uses Logical connective, logical operators such as Logical conjunction, conjunction (''and'') denoted as ∧, Logical disjunction, disjunction (''or'') denoted as ∨, and the negation (''not'') denoted as ¬. Elementary algebra, on the other hand, uses arithmetic operators such as addition, multiplication, subtraction and division. So Boolean algebra is a formal way of describing logical operations, in the same way that elementary algebra describes numerical operations. Boolean algebra was introduced by George Boole in his first book ''The Mathematical Analysis of Logic'' (1847), and set forth more fully in his ''The Laws of Thought, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uncertainty
Uncertainty refers to epistemic situations involving imperfect or unknown information. It applies to predictions of future events, to physical measurements that are already made, or to the unknown. Uncertainty arises in partially observable or stochastic environments, as well as due to ignorance, indolence, or both. It arises in any number of fields, including insurance, philosophy, physics, statistics, economics, finance, medicine, psychology, sociology, engineering, metrology, meteorology, ecology and information science. Concepts Although the terms are used in various ways among the general public, many specialists in decision theory, statistics and other quantitative fields have defined uncertainty, risk, and their measurement as: Uncertainty The lack of certainty, a state of limited knowledge where it is impossible to exactly describe the existing state, a future outcome, or more than one possible outcome. ;Measurement of uncertainty: A set of possible states or outc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Interval Arithmetic
Interval arithmetic (also known as interval mathematics, interval analysis, or interval computation) is a mathematical technique used to put bounds on rounding errors and measurement errors in mathematical computation. Numerical methods using interval arithmetic can guarantee reliable and mathematically correct results. Instead of representing a value as a single number, interval arithmetic represents each value as a range of possibilities. For example, instead of saying the height of someone is approximately 2 meters, one could using interval arithmetic, say that the height of the person is definitely between 1.97 meters and 2.03 meters. Mathematically, using interval arithmetic, instead of working with an uncertain real-valued variable x, one works with an interval ,b/math> that defines the range of values that x can have. In other words, any value of the variable x lies in the closed interval between a and b. A function f, when applied to x, yields an inexact value; f ins ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fuzzy Set
In mathematics, fuzzy sets (a.k.a. uncertain sets) are sets whose elements have degrees of membership. Fuzzy sets were introduced independently by Lotfi A. Zadeh in 1965 as an extension of the classical notion of set. At the same time, defined a more general kind of structure called an ''L''-relation, which he studied in an abstract algebraic context. Fuzzy relations, which are now used throughout fuzzy mathematics and have applications in areas such as linguistics , decision-making , and clustering , are special cases of ''L''-relations when ''L'' is the unit interval , 1 In classical set theory, the membership of elements in a set is assessed in binary terms according to a bivalent condition—an element either belongs or does not belong to the set. By contrast, fuzzy set theory permits the gradual assessment of the membership of elements in a set; this is described with the aid of a membership function valued in the real unit interval , 1 Fuzzy sets generali ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uncertainty
Uncertainty refers to epistemic situations involving imperfect or unknown information. It applies to predictions of future events, to physical measurements that are already made, or to the unknown. Uncertainty arises in partially observable or stochastic environments, as well as due to ignorance, indolence, or both. It arises in any number of fields, including insurance, philosophy, physics, statistics, economics, finance, medicine, psychology, sociology, engineering, metrology, meteorology, ecology and information science. Concepts Although the terms are used in various ways among the general public, many specialists in decision theory, statistics and other quantitative fields have defined uncertainty, risk, and their measurement as: Uncertainty The lack of certainty, a state of limited knowledge where it is impossible to exactly describe the existing state, a future outcome, or more than one possible outcome. ;Measurement of uncertainty: A set of possible states or outc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Interval Arithmetic
Interval arithmetic (also known as interval mathematics, interval analysis, or interval computation) is a mathematical technique used to put bounds on rounding errors and measurement errors in mathematical computation. Numerical methods using interval arithmetic can guarantee reliable and mathematically correct results. Instead of representing a value as a single number, interval arithmetic represents each value as a range of possibilities. For example, instead of saying the height of someone is approximately 2 meters, one could using interval arithmetic, say that the height of the person is definitely between 1.97 meters and 2.03 meters. Mathematically, using interval arithmetic, instead of working with an uncertain real-valued variable x, one works with an interval ,b/math> that defines the range of values that x can have. In other words, any value of the variable x lies in the closed interval between a and b. A function f, when applied to x, yields an inexact value; f ins ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Random Variable
A random variable (also called random quantity, aleatory variable, or stochastic variable) is a mathematical formalization of a quantity or object which depends on random events. It is a mapping or a function from possible outcomes (e.g., the possible upper sides of a flipped coin such as heads H and tails T) in a sample space (e.g., the set \) to a measurable space, often the real numbers (e.g., \ in which 1 corresponding to H and -1 corresponding to T). Informally, randomness typically represents some fundamental element of chance, such as in the roll of a dice; it may also represent uncertainty, such as measurement error. However, the interpretation of probability is philosophically complicated, and even in specific cases is not always straightforward. The purely mathematical analysis of random variables is independent of such interpretational difficulties, and can be based upon a rigorous axiomatic setup. In the formal mathematical language of measure theory, a random var ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |