Fuzzy Number on:
[Wikipedia]
[Google]
[Amazon]
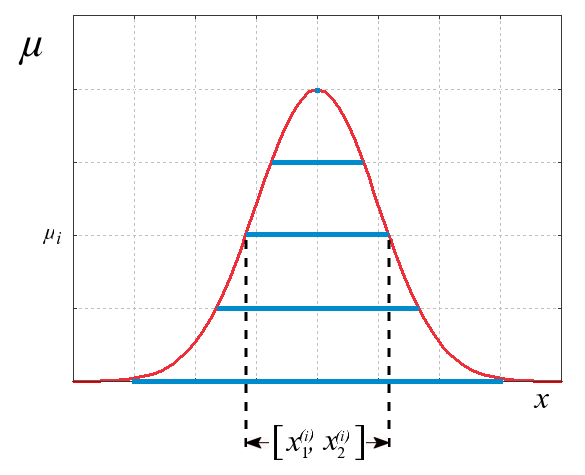A fuzzy number is a generalization of a regular
Fuzzy Logic Tutorial
Fuzzy logic Numbers Real numbers {{num-stub
A fuzzy number is a generalization of a regular real number
In mathematics, a real number is a number that can be used to measurement, measure a ''continuous'' one-dimensional quantity such as a distance, time, duration or temperature. Here, ''continuous'' means that values can have arbitrarily small var ...
in the sense that it does not refer to one single value but rather to a connected set of possible values, where each possible value has its own weight between 0 and 1. This weight is called the membership function
In mathematics, an indicator function or a characteristic function of a subset of a set is a function that maps elements of the subset to one, and all other elements to zero. That is, if is a subset of some set , one has \mathbf_(x)=1 if x\ ...
. A fuzzy number is thus a special case of a convex, normalized fuzzy set
In mathematics, fuzzy sets (a.k.a. uncertain sets) are sets whose elements have degrees of membership. Fuzzy sets were introduced independently by Lotfi A. Zadeh in 1965 as an extension of the classical notion of set.
At the same time, defined ...
of the real line
In elementary mathematics, a number line is a picture of a graduated straight line that serves as visual representation of the real numbers. Every point of a number line is assumed to correspond to a real number, and every real number to a po ...
. Just like fuzzy logic
Fuzzy logic is a form of many-valued logic in which the truth value of variables may be any real number between 0 and 1. It is employed to handle the concept of partial truth, where the truth value may range between completely true and complet ...
is an extension of Boolean logic
In mathematics and mathematical logic, Boolean algebra is a branch of algebra. It differs from elementary algebra in two ways. First, the values of the variables are the truth values ''true'' and ''false'', usually denoted 1 and 0, whereas in ...
(which uses absolute truth and falsehood only, and nothing in between), fuzzy numbers are an extension of real numbers. Calculations with fuzzy numbers allow the incorporation of uncertainty
Uncertainty refers to Epistemology, epistemic situations involving imperfect or unknown information. It applies to predictions of future events, to physical measurements that are already made, or to the unknown. Uncertainty arises in partially ...
on parameters, properties, geometry, initial conditions, etc. The arithmetic calculations on fuzzy numbers are implemented using fuzzy arithmetic operations, which can be done by two different approaches: (1) interval arithmetic
Interval arithmetic (also known as interval mathematics, interval analysis, or interval computation) is a mathematical technique used to put bounds on rounding errors and measurement errors in mathematical computation. Numerical methods usin ...
approach; and (2) the extension principle approach.
A fuzzy number is equal to a fuzzy interval. The degree of fuzziness is determined by the a-cut which is also called the fuzzy spread.
See also
*Fuzzy set
In mathematics, fuzzy sets (a.k.a. uncertain sets) are sets whose elements have degrees of membership. Fuzzy sets were introduced independently by Lotfi A. Zadeh in 1965 as an extension of the classical notion of set.
At the same time, defined ...
* Uncertainty
Uncertainty refers to Epistemology, epistemic situations involving imperfect or unknown information. It applies to predictions of future events, to physical measurements that are already made, or to the unknown. Uncertainty arises in partially ...
* Interval arithmetic
Interval arithmetic (also known as interval mathematics, interval analysis, or interval computation) is a mathematical technique used to put bounds on rounding errors and measurement errors in mathematical computation. Numerical methods usin ...
* Random variable
A random variable (also called random quantity, aleatory variable, or stochastic variable) is a mathematical formalization of a quantity or object which depends on random events. It is a mapping or a function from possible outcomes (e.g., the p ...
References
External links
Fuzzy Logic Tutorial
Fuzzy logic Numbers Real numbers {{num-stub