|
Functional Graph
In graph theory, a pseudoforest is an undirected graphThe kind of undirected graph considered here is often called a multigraph or pseudograph, to distinguish it from a simple graph. in which every connected component has at most one cycle. That is, it is a system of vertices and edges connecting pairs of vertices, such that no two cycles of consecutive edges share any vertex with each other, nor can any two cycles be connected to each other by a path of consecutive edges. A pseudotree is a connected pseudoforest. The names are justified by analogy to the more commonly studied trees and forests. (A tree is a connected graph with no cycles; a forest is a disjoint union of trees.) Gabow and Tarjan. attribute the study of pseudoforests to Dantzig's 1963 book on linear programming, in which pseudoforests arise in the solution of certain network flow problems.. Pseudoforests also form graph-theoretic models of functions and occur in several algorithmic problems. Pseudoforests a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pseudoforest
In graph theory, a pseudoforest is an undirected graphThe kind of undirected graph considered here is often called a multigraph or pseudograph, to distinguish it from a simple graph. in which every connected component has at most one cycle. That is, it is a system of vertices and edges connecting pairs of vertices, such that no two cycles of consecutive edges share any vertex with each other, nor can any two cycles be connected to each other by a path of consecutive edges. A pseudotree is a connected pseudoforest. The names are justified by analogy to the more commonly studied trees and forests. (A tree is a connected graph with no cycles; a forest is a disjoint union of trees.) Gabow and Tarjan. attribute the study of pseudoforests to Dantzig's 1963 book on linear programming, in which pseudoforests arise in the solution of certain network flow problems.. Pseudoforests also form graph-theoretic models of functions and occur in several algorithmic problems. Pseudoforest ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Edge (graph Theory)
This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges. Symbols A B C D E F G H I K L M N O ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conway's Thrackle Conjecture
A thrackle is an embedding of a graph in the plane, such that each edge is a Jordan arc and every pair of edges meet exactly once. Edges may either meet at a common endpoint, or, if they have no endpoints in common, at a point in their interiors. In the latter case, the crossing must be '' transverse''.. A preliminary version of these results was reviewed in . Linear thrackles A linear thrackle is a thrackle drawn in such a way that its edges are straight line segments. As Paul Erdős observed, every linear thrackle has at most as many edges as vertices. If a vertex ''v'' is connected to three or more edges ''vw'', ''vx'', and ''vy'', at least one of those edges (say ''vw'') lies on a line that separates two other edges. Then, ''w'' must have degree one, because no line segment ending at ''w'', other than ''vw'', can touch both ''vx'' and ''vy''. Removing ''w'' and ''vw'' produces a smaller thrackle, without changing the difference between the numbers of edges and vertices. Aft ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graph Drawing
Graph drawing is an area of mathematics and computer science combining methods from geometric graph theory and information visualization to derive two-dimensional depictions of graphs arising from applications such as social network analysis, cartography, linguistics, and bioinformatics. A drawing of a graph or network diagram is a pictorial representation of the vertices and edges of a graph. This drawing should not be confused with the graph itself: very different layouts can correspond to the same graph., p. 6. In the abstract, all that matters is which pairs of vertices are connected by edges. In the concrete, however, the arrangement of these vertices and edges within a drawing affects its understandability, usability, fabrication cost, and aesthetics. The problem gets worse if the graph changes over time by adding and deleting edges (dynamic graph drawing) and the goal is to preserve the user's mental map. Graphical conventions Graphs are frequently drawn as node–link ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thrackle
A thrackle is an embedding of a graph in the plane, such that each edge is a Jordan arc and every pair of edges meet exactly once. Edges may either meet at a common endpoint, or, if they have no endpoints in common, at a point in their interiors. In the latter case, the crossing must be '' transverse''.. A preliminary version of these results was reviewed in . Linear thrackles A linear thrackle is a thrackle drawn in such a way that its edges are straight line segments. As Paul Erdős observed, every linear thrackle has at most as many edges as vertices. If a vertex ''v'' is connected to three or more edges ''vw'', ''vx'', and ''vy'', at least one of those edges (say ''vw'') lies on a line that separates two other edges. Then, ''w'' must have degree one, because no line segment ending at ''w'', other than ''vw'', can touch both ''vx'' and ''vy''. Removing ''w'' and ''vw'' produces a smaller thrackle, without changing the difference between the numbers of edges and vertices. Aft ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Induced Subgraph
In the mathematical field of graph theory, an induced subgraph of a graph is another graph, formed from a subset of the vertices of the graph and ''all'' of the edges (from the original graph) connecting pairs of vertices in that subset. Definition Formally, let G=(V,E) be any graph, and let S\subset V be any subset of vertices of . Then the induced subgraph G is the graph whose vertex set is S and whose edge set consists of all of the edges in E that have both endpoints in S . That is, for any two vertices u,v\in S , u and v are adjacent in G if and only if they are adjacent in G . The same definition works for undirected graphs, directed graphs, and even multigraphs. The induced subgraph G may also be called the subgraph induced in G by S , or (if context makes the choice of G unambiguous) the induced subgraph of S . Examples Important types of induced subgraphs include the following. * Induced paths are induced subgraphs that are paths. The shortest path betwe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
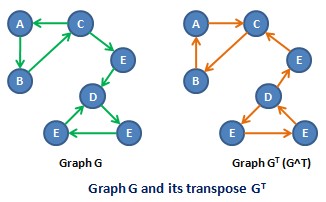
Transpose Graph
In the mathematical and algorithmic study of graph theory, the converse, transpose or reverse, entry 2.24 of a directed graph is another directed graph on the same set of vertices with all of the edges reversed compared to the orientation of the corresponding edges in . That is, if contains an edge then the converse/transpose/reverse of contains an edge and vice versa. Notation The name arises because the reversal of arrows corresponds to taking the converse of an implication in logic. The name is because the adjacency matrix of the transpose directed graph is the transpose of the adjacency matrix of the original directed graph. There is no general agreement on preferred terminology. The converse is denoted symbolically as , , , or other notations, depending on which terminology is used and which book or article is the source for the notation. Applications Although there is little difference mathematically between a graph and its transpose, the difference may b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graphs Of Functions
In mathematics, the graph of a function f is the set of ordered pairs (x, y), where f(x) = y. In the common case where x and f(x) are real numbers, these pairs are Cartesian coordinates of points in two-dimensional space and thus form a subset of this plane. In the case of functions of two variables, that is functions whose domain consists of pairs (x, y), the graph usually refers to the set of ordered triples (x, y, z) where f(x,y) = z, instead of the pairs ((x, y), z) as in the definition above. This set is a subset of three-dimensional space; for a continuous real-valued function of two real variables, it is a surface. In science, engineering, technology, finance, and other areas, graphs are tools used for many purposes. In the simplest case one variable is plotted as a function of another, typically using rectangular axes; see ''Plot (graphics)'' for details. A graph of a function is a special case of a relation. In the modern foundations of mathematics, and, t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Outdegree
In mathematics, and more specifically in graph theory, a directed graph (or digraph) is a graph that is made up of a set of vertices connected by directed edges, often called arcs. Definition In formal terms, a directed graph is an ordered pair where * ''V'' is a set whose elements are called '' vertices'', ''nodes'', or ''points''; * ''A'' is a set of ordered pairs of vertices, called ''arcs'', ''directed edges'' (sometimes simply ''edges'' with the corresponding set named ''E'' instead of ''A''), ''arrows'', or ''directed lines''. It differs from an ordinary or undirected graph, in that the latter is defined in terms of unordered pairs of vertices, which are usually called ''edges'', ''links'' or ''lines''. The aforementioned definition does not allow a directed graph to have multiple arrows with the same source and target nodes, but some authors consider a broader definition that allows directed graphs to have such multiple arcs (namely, they allow the arc set to be a m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Directed Graph
In mathematics, and more specifically in graph theory, a directed graph (or digraph) is a graph that is made up of a set of vertices connected by directed edges, often called arcs. Definition In formal terms, a directed graph is an ordered pair where * ''V'' is a set whose elements are called '' vertices'', ''nodes'', or ''points''; * ''A'' is a set of ordered pairs of vertices, called ''arcs'', ''directed edges'' (sometimes simply ''edges'' with the corresponding set named ''E'' instead of ''A''), ''arrows'', or ''directed lines''. It differs from an ordinary or undirected graph, in that the latter is defined in terms of unordered pairs of vertices, which are usually called ''edges'', ''links'' or ''lines''. The aforementioned definition does not allow a directed graph to have multiple arrows with the same source and target nodes, but some authors consider a broader definition that allows directed graphs to have such multiple arcs (namely, they allow the arc set to be a m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tree (graph Theory)
In graph theory, a tree is an undirected graph in which any two vertices are connected by ''exactly one'' path, or equivalently a connected acyclic undirected graph. A forest is an undirected graph in which any two vertices are connected by ''at most one'' path, or equivalently an acyclic undirected graph, or equivalently a disjoint union of trees. A polytreeSee . (or directed tree or oriented treeSee .See . or singly connected networkSee .) is a directed acyclic graph (DAG) whose underlying undirected graph is a tree. A polyforest (or directed forest or oriented forest) is a directed acyclic graph whose underlying undirected graph is a forest. The various kinds of data structures referred to as trees in computer science have underlying graphs that are trees in graph theory, although such data structures are generally rooted trees. A rooted tree may be directed, called a directed rooted tree, either making all its edges point away from the root—in which case it is call ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
The21
''The'' () is a grammatical article in English, denoting persons or things that are already or about to be mentioned, under discussion, implied or otherwise presumed familiar to listeners, readers, or speakers. It is the definite article in English. ''The'' is the most frequently used word in the English language; studies and analyses of texts have found it to account for seven percent of all printed English-language words. It is derived from gendered articles in Old English which combined in Middle English and now has a single form used with nouns of any gender. The word can be used with both singular and plural nouns, and with a noun that starts with any letter. This is different from many other languages, which have different forms of the definite article for different genders or numbers. Pronunciation In most dialects, "the" is pronounced as (with the voiced dental fricative followed by a schwa) when followed by a consonant sound, and as (homophone of the archai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.png "Click for more on -> The21")