|
Fresnel Integrals
250px, Plots of and . The maximum of is about . If the integrands of and were defined using instead of , then the image would be scaled vertically and horizontally (see below). The Fresnel integrals and are two transcendental functions named after Augustin-Jean Fresnel that are used in optics and are closely related to the error function (). They arise in the description of near-field Fresnel diffraction phenomena and are defined through the following integral representations: S(x) = \int_0^x \sin\left(t^2\right)\,dt, \quad C(x) = \int_0^x \cos\left(t^2\right)\,dt. The simultaneous parametric plot of and is the Euler spiral (also known as the Cornu spiral or clothoid). Definition 250px, Fresnel integrals with arguments instead of converge to instead of . The Fresnel integrals admit the following power series expansions that converge for all : \begin S(x) &= \int_0^x \sin\left(t^2\right)\,dt = \sum_^(-1)^n \frac, \\ C(x) &= \int_0^x \cos\left(t^2\right)\,dt = ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fresnel Integrals (Unnormalised)
image:Fresnel Integrals (Unnormalised).svg, 250px, Plots of and . The maximum of is about . If the integrands of and were defined using instead of , then the image would be scaled vertically and horizontally (see below). The Fresnel integrals and are two transcendental functions named after Augustin-Jean Fresnel that are used in optics and are closely related to the error function (). They arise in the description of near and far field, near-field Fresnel diffraction phenomena and are defined through the following integral representations: S(x) = \int_0^x \sin\left(t^2\right)\,dt, \quad C(x) = \int_0^x \cos\left(t^2\right)\,dt. The simultaneous parametric equation, parametric plot of and is the Euler spiral (also known as the Cornu spiral or clothoid). Definition image:Fresnel Integrals (Normalised).svg, 250px, Fresnel integrals with arguments instead of converge to instead of . The Fresnel integrals admit the following power series expansions that converge for al ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Marie Alfred Cornu
Marie Alfred Cornu (; 6 March 1841 – 12 April 1902) was a French physicist. The French generally refer to him as Alfred Cornu. Life Cornu was born at Orléans to François Cornu and Sophie Poinsellier. He was educated at the École polytechnique and the École des mines. Upon the death of Émile Verdet in 1866, Cornu became, in 1867, Verdet's successor as professor of experimental physics at the École polytechnique, where he remained throughout his life. Although he made various excursions into other branches of physical science, undertaking, for example, with Jean-Baptistin Baille about 1870 a repetition of Cavendish's experiment for determining the gravitational constant ''G'', his original work was mainly concerned with optics and spectroscopy. In particular he carried out a classical redetermination of the speed of light by A. H. L. Fizeau's method (see Fizeau-Foucault Apparatus), introducing various improvements in the apparatus, which added greatly to the accuracy of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fresnel S With Domain Coloring
Augustin-Jean Fresnel (10 May 1788 – 14 July 1827) was a French civil engineer and physicist whose research in optics led to the almost unanimous acceptance of the wave theory of light, excluding any remnant of Isaac Newton, Newton's corpuscular theory of light, corpuscular theory, from the late 1830s until the end of the 19th century. He is perhaps better known for inventing the Catadioptric system, catadioptric (reflective/refractive) Fresnel lens and for pioneering the use of "stepped" lenses to extend the visibility of lighthouses, saving countless lives at sea. The simpler Dioptrics, dioptric (purely refractive) stepped lens, first proposed by Georges-Louis Leclerc, Comte de Buffon, Count Buffon and independently reinvented by Fresnel, is used in screen magnifying glass, magnifiers and in condenser lenses for overhead projectors. By expressing Christiaan Huygens, Huygens's principle of secondary waves and Thomas Young (scientist), Young's principle of interference ( ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Odd Function
In mathematics, even functions and odd functions are functions which satisfy particular symmetry relations, with respect to taking additive inverses. They are important in many areas of mathematical analysis, especially the theory of power series and Fourier series. They are named for the parity of the powers of the power functions which satisfy each condition: the function f(x) = x^n is an even function if ''n'' is an even integer, and it is an odd function if ''n'' is an odd integer. Definition and examples Evenness and oddness are generally considered for real functions, that is real-valued functions of a real variable. However, the concepts may be more generally defined for functions whose domain and codomain both have a notion of additive inverse. This includes abelian groups, all rings, all fields, and all vector spaces. Thus, for example, a real function could be odd or even (or neither), as could a complex-valued function of a vector variable, and so on. The given e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Clothoid Loop
The generic roller coaster vertical loop, where a section of track causes the riders to complete a 360 degree turn, is the most basic of roller coaster inversions. At the top of the loop, riders are completely inverted. History The vertical loop is not a recent roller coaster innovation. Its origins can be traced back to the 1850s when '' centrifugal railways'' were built in France and Great Britain. The rides relied on centrifugal forces to hold the car in the loop. One early looping coaster was shut down after an accident. Later attempts to build a looping roller coaster were carried out during the late 19th century with the ''Flip Flap Railway'' at Sea Lion Park. The ride was designed with a completely circular loop (rather than the teardrop shape used by many modern looping roller coasters), and caused neck injuries due to the intense G-forces pulled with the tight radius of the loop. The next attempt at building a looping roller coaster was in 1901 when Edwin Prescott bui ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rollercoaster
A roller coaster, or rollercoaster, is a type of amusement ride that employs a form of elevated railroad track designed with tight turns, steep slopes, and sometimes inversions. Passengers ride along the track in open cars, and the rides are often found in amusement parks and theme parks around the world. LaMarcus Adna Thompson obtained one of the first known patents for a roller coaster design in 1885, related to the Switchback Railway that opened a year earlier at Coney Island. The track in a coaster design does not necessarily have to be a complete circuit, as shuttle roller coasters demonstrate. Most roller coasters have multiple cars in which passengers sit and are restrained. Two or more cars hooked together are called a train. Some roller coasters, notably Wild Mouse roller coasters, run with single cars. History The Russian mountain and the Aerial Promenades The oldest roller coasters are believed to have originated from the so-called " Russian Mountains", spec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angular Acceleration
In physics, angular acceleration refers to the time rate of change of angular velocity. As there are two types of angular velocity, namely spin angular velocity and orbital angular velocity, there are naturally also two types of angular acceleration, called spin angular acceleration and orbital angular acceleration respectively. Spin angular acceleration refers to the angular acceleration of a rigid body about its centre of rotation, and orbital angular acceleration refers to the angular acceleration of a point particle about a fixed origin. Angular acceleration is measured in units of angle per unit time squared (which in SI units is radians per second squared), and is usually represented by the symbol alpha (α). In two dimensions, angular acceleration is a pseudoscalar whose sign is taken to be positive if the angular speed increases counterclockwise or decreases clockwise, and is taken to be negative if the angular speed increases clockwise or decreases counterclockwise. I ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
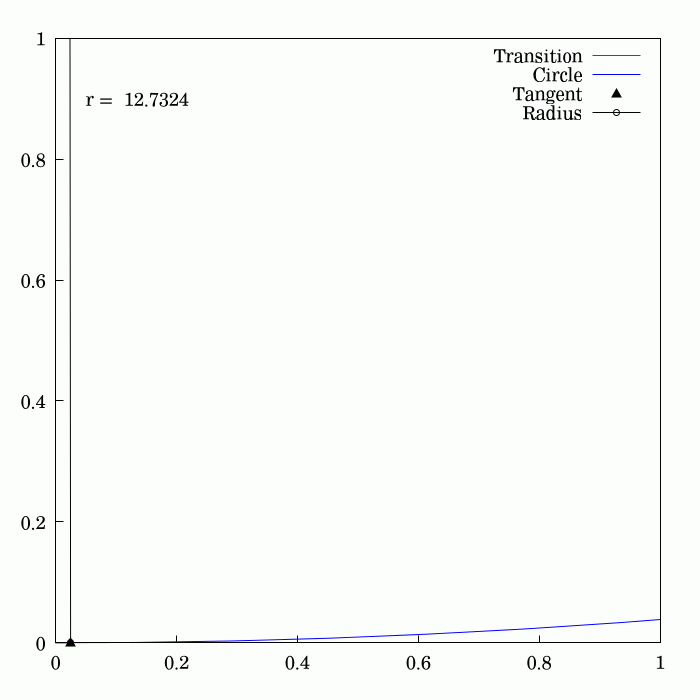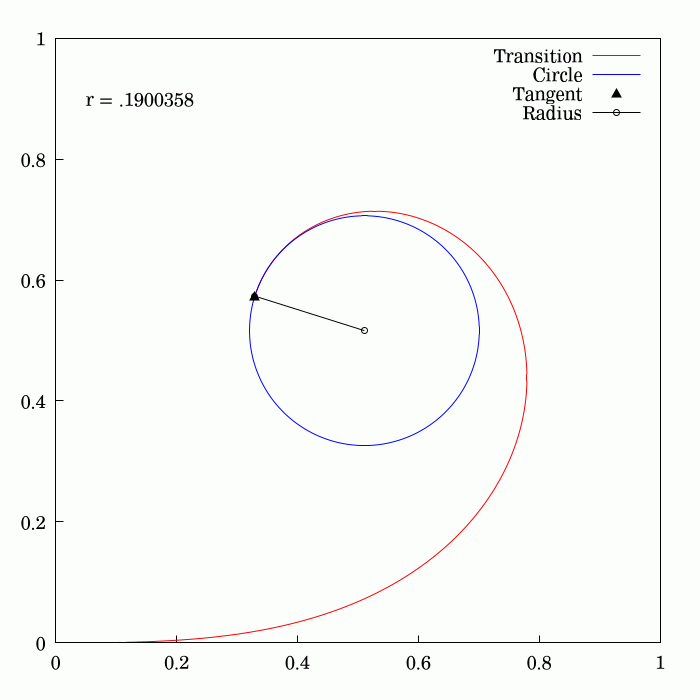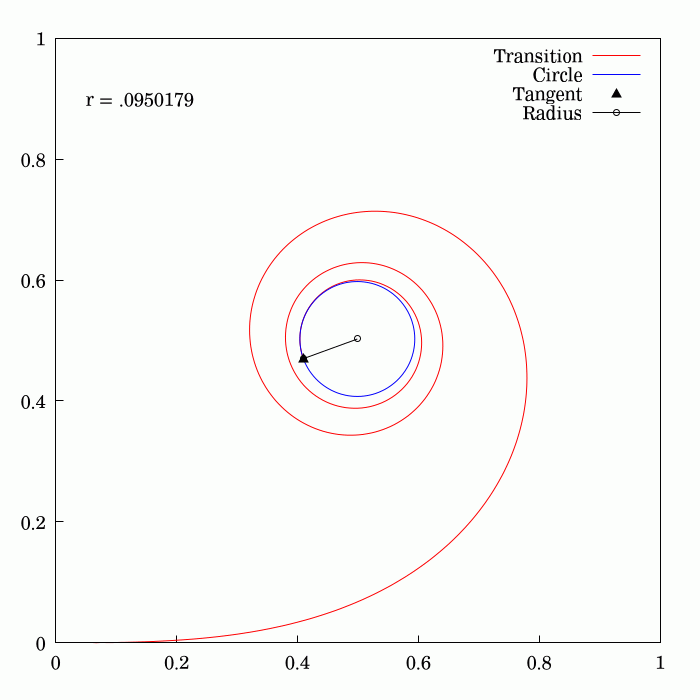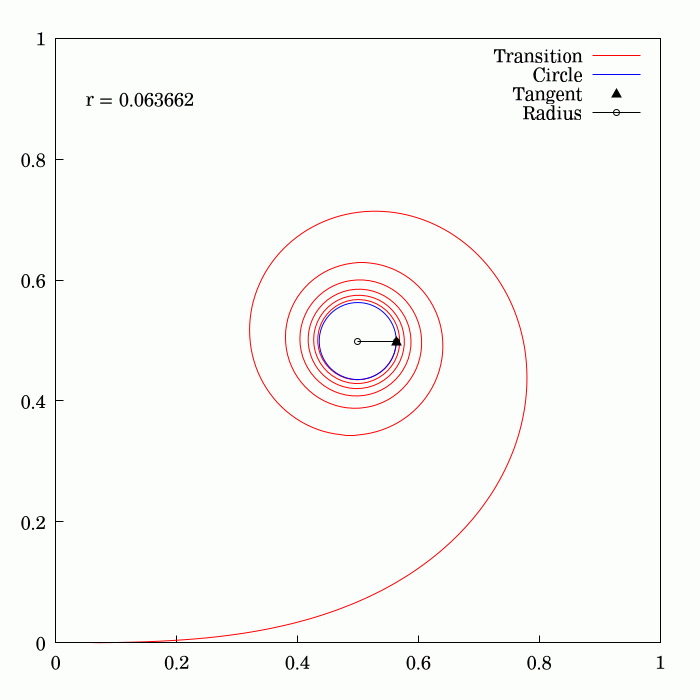
Track Transition Curve
A track transition curve, or spiral easement, is a mathematically-calculated curve on a section of highway, or railroad track, in which a straight section changes into a curve. It is designed to prevent sudden changes in lateral (or centripetal) acceleration. In plane (viewed from above), the start of the transition of the horizontal curve is at infinite radius, and at the end of the transition, it has the same radius as the curve itself and so forms a very broad spiral. At the same time, in the vertical plane, the outside of the curve is gradually raised until the correct degree of bank is reached. If such an easement were not applied, the lateral acceleration of a rail vehicle would change abruptly at one point (the tangent point where the straight track meets the curve) with undesirable results. With a road vehicle, a transition curve allows the driver to alter the steering in a gradual manner. History On early railroads, because of the low speeds and wide-radius curves em ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Curvature
In mathematics, curvature is any of several strongly related concepts in geometry. Intuitively, the curvature is the amount by which a curve deviates from being a straight line, or a surface deviates from being a plane. For curves, the canonical example is that of a circle, which has a curvature equal to the reciprocal of its radius. Smaller circles bend more sharply, and hence have higher curvature. The curvature ''at a point'' of a differentiable curve is the curvature of its osculating circle, that is the circle that best approximates the curve near this point. The curvature of a straight line is zero. In contrast to the tangent, which is a vector quantity, the curvature at a point is typically a scalar quantity, that is, it is expressed by a single real number. For surfaces (and, more generally for higher-dimensional manifolds), that are embedded in a Euclidean space, the concept of curvature is more complex, as it depends on the choice of a direction on the surface or man ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tangent Vector
In mathematics, a tangent vector is a vector that is tangent to a curve or surface at a given point. Tangent vectors are described in the differential geometry of curves in the context of curves in R''n''. More generally, tangent vectors are elements of a tangent space of a differentiable manifold. Tangent vectors can also be described in terms of germs. Formally, a tangent vector at the point x is a linear derivation of the algebra defined by the set of germs at x. Motivation Before proceeding to a general definition of the tangent vector, we discuss its use in calculus and its tensor properties. Calculus Let \mathbf(t) be a parametric smooth curve. The tangent vector is given by \mathbf'(t), where we have used a prime instead of the usual dot to indicate differentiation with respect to parameter . The unit tangent vector is given by \mathbf(t) = \frac\,. Example Given the curve \mathbf(t) = \left\ in \R^3, the unit tangent vector at t = 0 is given by \mathbf(0) = \frac = ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.jpeg/1200px-Brusio_Viaduct_(158241421).jpeg "Click for more on -> Track Transition Curve")
