|
Fractional-order Control
Fractional-order control (FOC) is a field of control theory that uses the fractional-order integrator as part of the control system design toolkit. The use of fractional calculus (FC) can improve and generalize well-established control methods and strategies. The fundamental advantage of FOC is that the fractional-order integrator weights history using a function that decays with a power-law tail. The effect is that the effects of all time are computed for each iteration of the control algorithm. This creates a 'distribution of time constants,' the upshot of which is there is no particular time constant, or resonance frequency, for the system. In fact, the fractional integral operator \frac is different from any integer-order rational transfer function (s), in the sense that it is a non-local operator that possesses an infinite memory and takes into account the whole history of its input signal. Fractional-order control shows promise in many controlled environments that suf ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Control Theory
Control theory is a field of mathematics that deals with the control of dynamical systems in engineered processes and machines. The objective is to develop a model or algorithm governing the application of system inputs to drive the system to a desired state, while minimizing any ''delay'', ''overshoot'', or ''steady-state error'' and ensuring a level of control stability; often with the aim to achieve a degree of optimality. To do this, a controller with the requisite corrective behavior is required. This controller monitors the controlled process variable (PV), and compares it with the reference or set point (SP). The difference between actual and desired value of the process variable, called the ''error'' signal, or SP-PV error, is applied as feedback to generate a control action to bring the controlled process variable to the same value as the set point. Other aspects which are also studied are controllability and observability. Control theory is used in control system eng ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fractional-order Integrator
A fractional-order integrator or just simply fractional integrator is an integrator device that calculates the fractional-order integral or derivative (usually called a differintegral) of an input. Differentiation or integration is a real or complex parameter. The fractional integrator is useful in fractional-order control where the history of the system under control is important to the control system output. Overview The differintegral function, :_a \mathbb^q_t \left( f(x) \right) includes the integer order differentiation and integration functions, and allows a continuous range of functions around them. The differintegral parameters are ''a'', ''t'', and ''q''. The parameters ''a'' and ''t'' describe the range over which to compute the result. The differintegral parameter ''q'' may be any real number or complex number. If ''q'' is greater than zero, the differintegral computes a derivative. If ''q'' is less than zero, the differintegral computes an integral. The integer or ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Control System
A control system manages, commands, directs, or regulates the behavior of other devices or systems using control loops. It can range from a single home heating controller using a thermostat controlling a domestic boiler to large industrial control systems which are used for controlling processes or machines. The control systems are designed via control engineering process. For continuously modulated control, a feedback controller is used to automatically control a process or operation. The control system compares the value or status of the process variable (PV) being controlled with the desired value or setpoint (SP), and applies the difference as a control signal to bring the process variable output of the plant to the same value as the setpoint. For sequential and combinational logic, software logic, such as in a programmable logic controller, is used. Open-loop and closed-loop control There are two common classes of control action: open loop and closed loop. In an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Power-law Tail
In statistics and business, a long tail of some distributions of numbers is the portion of the distribution having many occurrences far from the "head" or central part of the distribution. The distribution could involve popularities, random numbers of occurrences of events with various probabilities, etc. The term is often used loosely, with no definition or an arbitrary definition, but precise definitions are possible. In statistics, the term ''long-tailed distribution'' has a narrow technical meaning, and is a subtype of heavy-tailed distribution. Intuitively, a distribution is (right) long-tailed if, for any fixed amount, when a quantity exceeds a high level, it almost certainly exceeds it by at least that amount: large quantities are probably even larger. Note that there is no sense of ''the'' "long tail" of a distribution, but only the ''property'' of a distribution being long-tailed. In business, the term ''long tail'' is applied to rank-size distributions or rank-f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
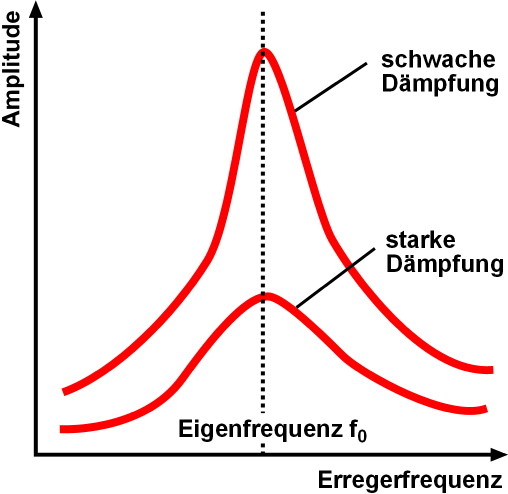
Resonance Frequency
Resonance describes the phenomenon of increased amplitude that occurs when the frequency of an applied periodic force (or a Fourier component of it) is equal or close to a natural frequency of the system on which it acts. When an oscillating force is applied at a resonant frequency of a dynamic system, the system will oscillate at a higher amplitude than when the same force is applied at other, non-resonant frequencies. Frequencies at which the response amplitude is a relative maximum are also known as resonant frequencies or resonance frequencies of the system. Small periodic forces that are near a resonant frequency of the system have the ability to produce large amplitude oscillations in the system due to the storage of vibrational energy. Resonance phenomena occur with all types of vibrations or waves: there is mechanical resonance, orbital resonance, acoustic resonance, electromagnetic resonance, nuclear magnetic resonance (NMR), electron spin resonance (ESR) and reson ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transfer Function
In engineering, a transfer function (also known as system function or network function) of a system, sub-system, or component is a function (mathematics), mathematical function that mathematical model, theoretically models the system's output for each possible input. They are widely used in electronics and control systems. In some simple cases, this function is a two-dimensional graph (function), graph of an independent scalar (mathematics), scalar input versus the dependent scalar output, called a transfer curve or characteristic curve. Transfer functions for components are used to design and analyze systems assembled from components, particularly using the block diagram technique, in electronics and control theory. The dimensions and units of the transfer function model the output response of the device for a range of possible inputs. For example, the transfer function of a two-port electronic circuit like an amplifier might be a two-dimensional graph of the scalar voltage at th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thermal Dissipation
All electronic devices and circuitry generate excess heat and thus require thermal management to improve reliability and prevent premature failure. The amount of heat output is equal to the power input, if there are no other energy interactions. There are several techniques for cooling including various styles of heat sinks, thermoelectric coolers, forced air systems and fans, heat pipes, and others. In cases of extreme low environmental temperatures, it may actually be necessary to heat the electronic components to achieve satisfactory operation. Overview Thermal resistance of devices This is usually quoted as the thermal resistance from junction to case of the semiconductor device. The units are °C/W. For example, a heatsink rated at 10 °C/W will get 10 °C hotter than the surrounding air when it dissipates 1 Watt of heat. Thus, a heatsink with a low °C/W value is more efficient than a heatsink with a high °C/W value. Given two semiconductor devi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
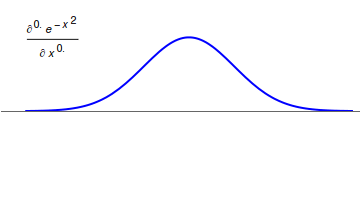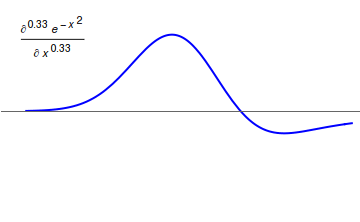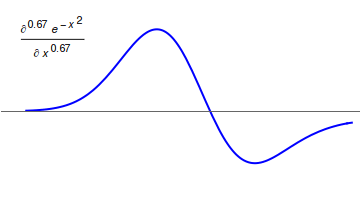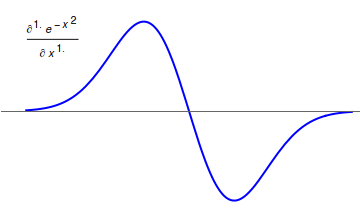
Differintegral
In fractional calculus, an area of mathematical analysis, the differintegral (sometime also called the derivigral) is a combined differentiation/integration operator. Applied to a function ƒ, the ''q''-differintegral of ''f'', here denoted by :\mathbb^q f is the fractional derivative (if ''q'' > 0) or fractional integral (if ''q'' So, \frac = \mathcal^\left\ which generalizes to \mathbb^qf(t) = \mathcal^\left\. Under the bilateral Laplace transform, here denoted by \mathcal and defined as \mathcal (t)=\int_^\infty e^ f(t)\, dt, differentiation transforms into a multiplication \mathcal\left frac\right= s\mathcal (t) Generalizing to arbitrary order and solving for \mathbb^qf(t), one obtains \mathbb^qf(t)=\mathcal^\left\. Representation via Newton series is the Newton interpolation over consecutive integer orders: \mathbb^qf(t) =\sum_^ \binom m \sum_^m\binom mk(-1)^f^(x). For fractional derivative definitions described in this section, the following identities hold: :\ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fractional Calculus
Fractional calculus is a branch of mathematical analysis that studies the several different possibilities of defining real number powers or complex number powers of the differentiation operator D :D f(x) = \frac f(x)\,, and of the integration operator J The symbol J is commonly used instead of the intuitive I in order to avoid confusion with other concepts identified by similar I–like glyphs, such as identities. :J f(x) = \int_0^x f(s) \,ds\,, and developing a calculus for such operators generalizing the classical one. In this context, the term ''powers'' refers to iterative application of a linear operator D to a function f, that is, repeatedly composing D with itself, as in D^n(f) = (\underbrace_n)(f) = \underbrace_n (f)\cdots))). For example, one may ask for a meaningful interpretation of :\sqrt = D^\frac12 as an analogue of the functional square root for the differentiation operator, that is, an expression for some linear operator that, when applied ''twice'' to any ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fractional-order System
In the fields of dynamical systems and control theory, a fractional-order system is a dynamical system that can be modeled by a fractional differential equation containing derivatives of non-integer order. Such systems are said to have ''fractional dynamics''. Derivatives and integrals of fractional orders are used to describe objects that can be characterized by power-law nonlocality, power-law long-range dependence or fractal properties. Fractional-order systems are useful in studying the anomalous behavior of dynamical systems in physics, electrochemistry, biology, viscoelasticity and chaotic systems. Definition A general dynamical system of fractional order can be written in the form : H(D^)(y_1,y_2,\ldots,y_l) = G(D^)(u_1,u_2,\ldots,u_k) where H and G are functions of the fractional derivative operator D of orders \alpha_1,\alpha_2,\ldots,\alpha_m and \beta_1,\beta_2,\ldots,\beta_n and y_i and u_j are functions of time. A common special case of this is the linear time ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Control Theory
Control theory is a field of mathematics that deals with the control of dynamical systems in engineered processes and machines. The objective is to develop a model or algorithm governing the application of system inputs to drive the system to a desired state, while minimizing any ''delay'', ''overshoot'', or ''steady-state error'' and ensuring a level of control stability; often with the aim to achieve a degree of optimality. To do this, a controller with the requisite corrective behavior is required. This controller monitors the controlled process variable (PV), and compares it with the reference or set point (SP). The difference between actual and desired value of the process variable, called the ''error'' signal, or SP-PV error, is applied as feedback to generate a control action to bring the controlled process variable to the same value as the set point. Other aspects which are also studied are controllability and observability. Control theory is used in control system eng ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |

.jpg)