|
Four-point Flexural Test
The four-point flexural test provides values for the modulus of elasticity in bending E_f, flexural stress \sigma_f, flexural strain \varepsilon_f and the flexural stress-strain response of the material. This test is very similar to the three-point bending flexural test. The major difference being that with the addition of a fourth bearing the portion of the beam between the two loading points is put under maximum stress, as opposed to only the material right under the central bearing in the case of three-point bending. This difference is of prime importance when studying brittle materials, where the number and severity of flaws exposed to the maximum stress is directly related to the flexural strength and crack initiation. Compared to the three-point bending flexural test, there are no shear forces in the four-point bending flexural test in the area between the two loading pins. The four-point bending test is therefore particularly suitable for brittle materials that cannot withs ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Flexural Modulus
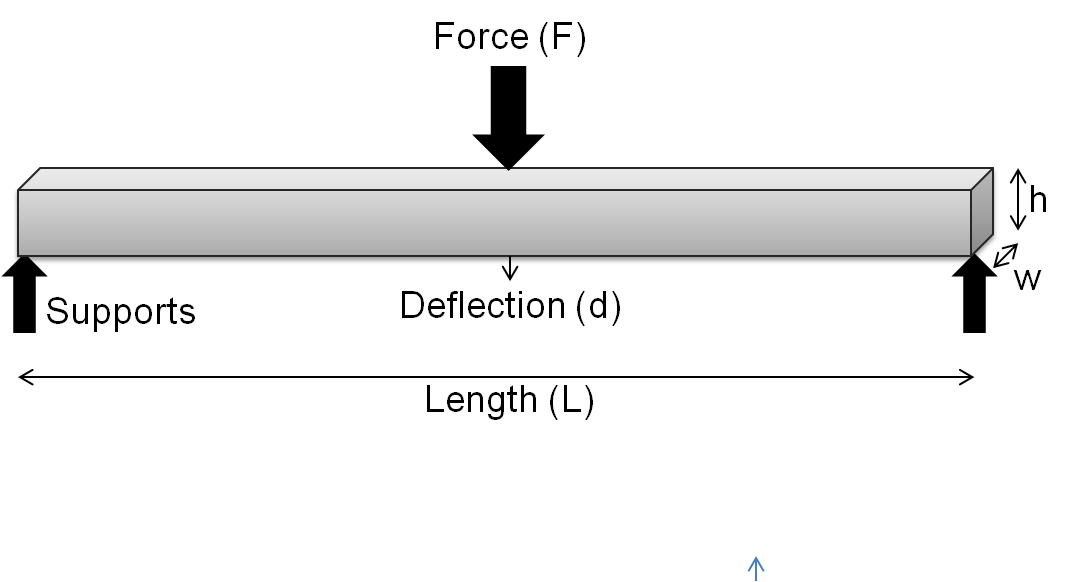
In mechanics, the flexural modulus or bending modulus is an intensive property that is computed as the ratio of stress to strain in flexural deformation, or the tendency for a material to resist bending. It is determined from the slope of a stress-strain curve produced by a flexural test (such as the ASTM D790), and uses units of force per area. The flexural modulus defined using the 2-point (cantilever) and 3-point bend tests assumes a linear stress strain response. For a 3-point test of a rectangular beam behaving as an isotropic linear material, where ''w'' and ''h'' are the width and height of the beam, ''I'' is the second moment of area of the beam's cross-section, ''L'' is the distance between the two outer supports, and ''d'' is the deflection due to the load ''F'' applied at the middle of the beam, the flexural modulus: : E_ = \frac From elastic beam theory :d = \frac and for rectangular beam : I = \fracwh^3 thus E_ = E ( Elastic modulus) For very small stra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Newton (unit)
The newton (symbol: N) is the unit of force in the International System of Units (SI). It is defined as 1 kg⋅m/s, the force which gives a mass of 1 kilogram an acceleration of 1 metre per second per second. It is named after Isaac Newton in recognition of his work on classical mechanics, specifically Newton's second law of motion. Definition A newton is defined as 1 kg⋅m/s (it is a derived unit which is defined in terms of the SI base units). One newton is therefore the force needed to accelerate one kilogram of mass at the rate of one metre per second squared in the direction of the applied force. The units "metre per second squared" can be understood as measuring a rate of change in velocity per unit of time, i.e. an increase in velocity by 1 metre per second every second. In 1946, Conférence Générale des Poids et Mesures (CGPM) Resolution 2 standardized the unit of force in the MKS system of units to be the amount needed to accelerate 1 kilogram of mass at the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
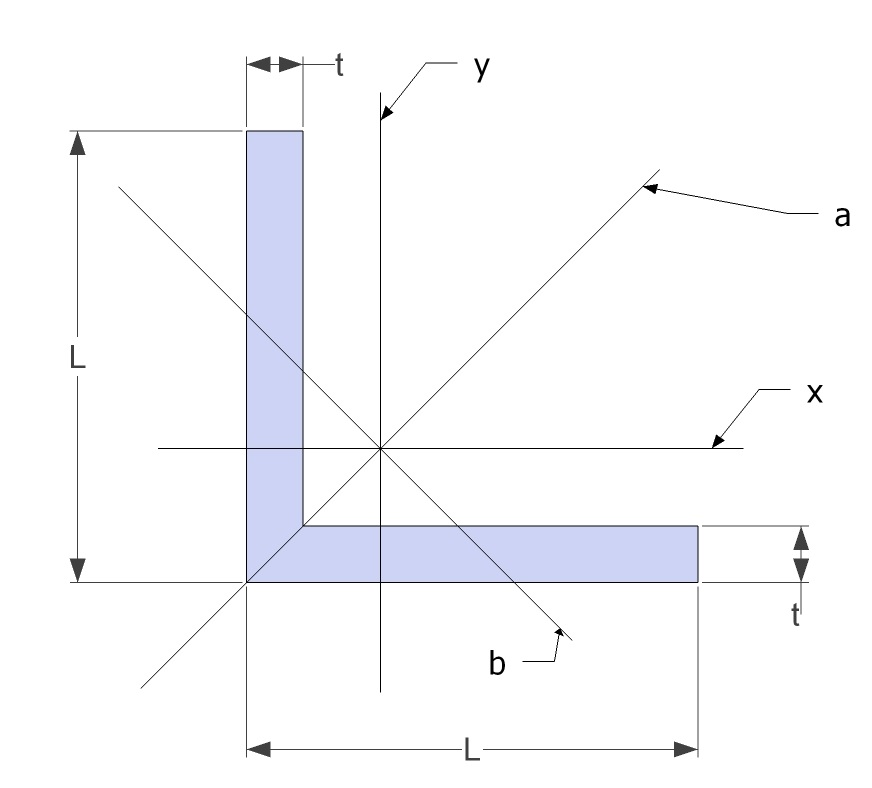
Second Moment Of Area
The second moment of area, or second area moment, or quadratic moment of area and also known as the area moment of inertia, is a geometrical property of an area which reflects how its points are distributed with regard to an arbitrary axis. The second moment of area is typically denoted with either an I (for an axis that lies in the plane of the area) or with a J (for an axis perpendicular to the plane). In both cases, it is calculated with a multiple integral over the object in question. Its dimension is L (length) to the fourth power. Its unit of dimension, when working with the International System of Units, is meters to the fourth power, m4, or inches to the fourth power, in4, when working in the Imperial System of Units. In structural engineering, the second moment of area of a beam is an important property used in the calculation of the beam's deflection and the calculation of stress caused by a moment applied to the beam. In order to maximize the second moment of a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Area Moments Of Inertia
The following is a list of second moments of area of some shapes. The second moment of area, also known as area moment of inertia, is a geometrical property of an area which reflects how its points are distributed with respect to an arbitrary axis. The unit of dimension of the second moment of area is length to fourth power, L4, and should not be confused with the mass moment of inertia. If the piece is thin, however, the mass moment of inertia equals the area density times the area moment of inertia. Second moments of area Please note that for the second moment of area equations in the below table: I_x = \iint_A y^2 \, dx \, dy and I_y = \iint_A x^2 \, dx \, dy. Parallel axis theorem The parallel axis theorem can be used to determine the second moment of area of a rigid body about any axis, given the body's second moment of area about a parallel axis through the body's centroid, the area of the cross section, and the perpendicular distance (''d'') between the axes. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Flexural Strength
Flexural strength, also known as modulus of rupture, or bend strength, or transverse rupture strength is a material property, defined as the stress in a material just before it yields in a flexure test. The transverse bending test is most frequently employed, in which a specimen having either a circular or rectangular cross-section is bent until fracture or yielding using a three-point flexural test technique. The flexural strength represents the highest stress experienced within the material at its moment of yield. It is measured in terms of stress, here given the symbol \sigma. Introduction When an object is formed of a single material, like a wooden beam or a steel rod, is bent (Fig. 1), it experiences a range of stresses across its depth (Fig. 2). At the edge of the object on the inside of the bend (concave face) the stress will be at its maximum compressive stress value. At the outside of the bend (convex face) the stress will be at its maximum tensile value. These ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bending
In applied mechanics, bending (also known as flexure) characterizes the behavior of a slender structural element subjected to an external load applied perpendicularly to a longitudinal axis of the element. The structural element is assumed to be such that at least one of its dimensions is a small fraction, typically 1/10 or less, of the other two.Boresi, A. P. and Schmidt, R. J. and Sidebottom, O. M., 1993, Advanced mechanics of materials, John Wiley and Sons, New York. When the length is considerably longer than the width and the thickness, the element is called a beam. For example, a closet rod sagging under the weight of clothes on clothes hangers is an example of a beam experiencing bending. On the other hand, a shell is a structure of any geometric form where the length and the width are of the same order of magnitude but the thickness of the structure (known as the 'wall') is considerably smaller. A large diameter, but thin-walled, short tube supported at its ends an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
ASTM
ASTM International, formerly known as American Society for Testing and Materials, is an international standards organization that develops and publishes voluntary consensus technical standards for a wide range of materials, products, systems, and services. Some 12,575 ASTM voluntary consensus standards operate globally. The organization's headquarters is in West Conshohocken, Pennsylvania, about northwest of Philadelphia. It is founded in 1902 as the American Section of the International Association for Testing Materials (see also International Organization for Standardization). History A group of scientists and engineers, led by Charles Dudley, formed ASTM in 1898 to address the frequent rail breaks affecting the fast-growing railroad industry. The group developed a standard for the steel used to fabricate rails. Originally called the "American Society for Testing Materials" in 1902, it became the "American Society for Testing And Materials" in 1961. In 2001, ASTM off ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Three-point Flexural Test
The three-point bending flexural test provides values for the modulus of elasticity in bending E_f, flexural stress \sigma_f, flexural strain \epsilon_f and the flexural stress–strain response of the material. This test is performed on a universal testing machine (tensile testing machine or tensile tester) with a three-point or four-point bend fixture. The main advantage of a three-point flexural test is the ease of the specimen preparation and testing. However, this method has also some disadvantages: the results of the testing method are sensitive to specimen and loading geometry and strain rate. Testing method The test method for conducting the test usually involves a specified test fixture on a universal testing machine. Details of the test preparation, conditioning, and conduct affect the test results. The sample is placed on two supporting pins a set distance apart. Calculation of the flexural stress \sigma_f :\sigma_f = \frac for a rectangular cross section :\si ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Toughness
In materials science and metallurgy, toughness is the ability of a material to absorb energy and plastically deform without fracturing."Toughness" Brian Larson, editor, 2001–2011, The Collaboration for NDT Education, Iowa State University [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Machining
Machining is a process in which a material (often metal) is cut to a desired final shape and size by a controlled material-removal process. The processes that have this common theme are collectively called subtractive manufacturing, which utilizes machine tools, in contrast to '' additive manufacturing'' (3D printing), which uses controlled addition of material. Machining is a part of the manufacture of many metal products, but it can also be used on other materials such as wood Wood is a porous and fibrous structural tissue found in the stems and roots of trees and other woody plants. It is an organic materiala natural composite of cellulose fibers that are strong in tension and embedded in a matrix of ligni ..., plastic, ceramic, and composite material. A person who specializes in machining is called a machinist. A room, building, or company where machining is done is called a machine shop. Much of modern-day machining is carried out by Numerical control, computer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |