|
Finite Volume Method For Unsteady Flow
Unsteady flows are characterized as flows in which the properties of the fluid are time dependent. It gets reflected in the governing equations as the time derivative of the properties are absent. For Studying Finite-volume method for unsteady flow there is some governing equations > Governing Equation The conservation equation for the transport of a scalar in unsteady flow has the general form as \frac + \operatorname\left(\rho \phi \upsilon\right) = \operatorname\left(\Gamma \operatorname \phi\right) + S_\phi \rho is density and \phi is conservative form of all fluid flow, \Gamma is the Diffusion coefficient and S is the Source term. \operatorname\left(\rho \phi \upsilon\right) is Net rate of flow of \phi out of fluid element(convection), \operatorname\left(\Gamma \operatorname \phi\right) is Rate of increase of \phi due to diffusion, S_\phi is Rate of increase of \phi due to sources. \frac is Rate of increase of \phi of fluid element(transient), The first ter ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Finite-volume Method
The finite volume method (FVM) is a method for representing and evaluating partial differential equations in the form of algebraic equations. In the finite volume method, volume integrals in a partial differential equation that contain a divergence term are converted to surface integrals, using the divergence theorem. These terms are then evaluated as fluxes at the surfaces of each finite volume. Because the flux entering a given volume is identical to that leaving the adjacent volume, these methods are conservative. Another advantage of the finite volume method is that it is easily formulated to allow for unstructured meshes. The method is used in many computational fluid dynamics packages. "Finite volume" refers to the small volume surrounding each node point on a mesh. Finite volume methods can be compared and contrasted with the finite difference methods, which approximate derivatives using nodal values, or finite element methods, which create local approximations of a soluti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Density
Density (volumetric mass density or specific mass) is the substance's mass per unit of volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' can also be used. Mathematically, density is defined as mass divided by volume: : \rho = \frac where ''ρ'' is the density, ''m'' is the mass, and ''V'' is the volume. In some cases (for instance, in the United States oil and gas industry), density is loosely defined as its weight per unit volume, although this is scientifically inaccurate – this quantity is more specifically called specific weight. For a pure substance the density has the same numerical value as its mass concentration. Different materials usually have different densities, and density may be relevant to buoyancy, purity and packaging. Osmium and iridium are the densest known elements at standard conditions for temperature and pressure. To simplify comparisons of density across different s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
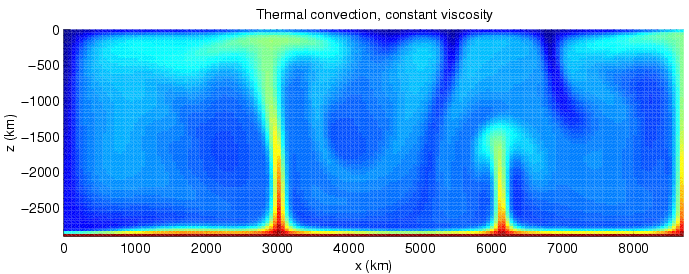
Convection
Convection is single or multiphase fluid flow that occurs spontaneously due to the combined effects of material property heterogeneity and body forces on a fluid, most commonly density and gravity (see buoyancy). When the cause of the convection is unspecified, convection due to the effects of thermal expansion and buoyancy can be assumed. Convection may also take place in soft solids or mixtures where particles can flow. Convective flow may be transient (such as when a multiphase mixture of oil and water separates) or steady state (see Convection cell). The convection may be due to gravitational, electromagnetic or fictitious body forces. Heat transfer by natural convection plays a role in the structure of Earth's atmosphere, its oceans, and its mantle. Discrete convective cells in the atmosphere can be identified by clouds, with stronger convection resulting in thunderstorms. Natural convection also plays a role in stellar physics. Convection is often categorised or d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diffusion
Diffusion is the net movement of anything (for example, atoms, ions, molecules, energy) generally from a region of higher concentration to a region of lower concentration. Diffusion is driven by a gradient in Gibbs free energy or chemical potential. It is possible to diffuse "uphill" from a region of lower concentration to a region of higher concentration, like in spinodal decomposition. The concept of diffusion is widely used in many fields, including physics (particle diffusion), chemistry, biology, sociology, economics, and finance (diffusion of people, ideas, and price values). The central idea of diffusion, however, is common to all of these: a substance or collection undergoing diffusion spreads out from a point or location at which there is a higher concentration of that substance or collection. A gradient is the change in the value of a quantity, for example, concentration, pressure, or temperature with the change in another variable, usually distance. A change in c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Control Volume
In continuum mechanics and thermodynamics, a control volume (CV) is a mathematical abstraction employed in the process of creating mathematical models of physical processes. In an inertial frame of reference, it is a fictitious region of a given volume fixed in space or moving with constant flow velocity through which the continuum (gas, liquid or solid) flows. The closed surface enclosing the region is referred to as the control surface. At steady state, a control volume can be thought of as an arbitrary volume in which the mass of the continuum remains constant. As a continuum moves through the control volume, the mass entering the control volume is equal to the mass leaving the control volume. At steady state, and in the absence of work and heat transfer, the energy within the control volume remains constant. It is analogous to the classical mechanics concept of the free body diagram. Overview Typically, to understand how a given physical law applies to the system under conside ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Steady State
In systems theory, a system or a Process theory, process is in a steady state if the variables (called state variables) which define the behavior of the system or the process are unchanging in time. In continuous time, this means that for those properties ''p'' of the system, the partial derivative with respect to time is zero and remains so: : \frac = 0 \quad \text t. In discrete time, it means that the first difference of each property is zero and remains so: :p_t-p_=0 \quad \text t. The concept of a steady state has relevance in many fields, in particular thermodynamics, Steady state economy, economics, and engineering. If a system is in a steady state, then the recently observed behavior of the system will continue into the future. In stochastic systems, the probabilities that various states will be repeated will remain constant. See for example Linear difference equation#Conversion to homogeneous form for the derivation of the steady state. In many systems, a steady state i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heat Conduction
Conduction is the process by which heat is transferred from the hotter end to the colder end of an object. The ability of the object to conduct heat is known as its ''thermal conductivity'', and is denoted . Heat spontaneously flows along a temperature gradient (i.e. from a hotter body to a colder body). For example, heat is conducted from the hotplate of an electric stove to the bottom of a saucepan in contact with it. In the absence of an opposing external driving energy source, within a body or between bodies, temperature differences decay over time, and thermal equilibrium is approached, temperature becoming more uniform. In conduction, the heat flow is within and through the body itself. In contrast, in heat transfer by thermal radiation, the transfer is often between bodies, which may be separated spatially. Heat can also be transferred by a combination of conduction and radiation. In solids, conduction is mediated by the combination of vibrations and collisions of molecu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Temperature
Temperature is a physical quantity that expresses quantitatively the perceptions of hotness and coldness. Temperature is measured with a thermometer. Thermometers are calibrated in various temperature scales that historically have relied on various reference points and thermometric substances for definition. The most common scales are the Celsius scale with the unit symbol °C (formerly called ''centigrade''), the Fahrenheit scale (°F), and the Kelvin scale (K), the latter being used predominantly for scientific purposes. The kelvin is one of the seven base units in the International System of Units (SI). Absolute zero, i.e., zero kelvin or −273.15 °C, is the lowest point in the thermodynamic temperature scale. Experimentally, it can be approached very closely but not actually reached, as recognized in the third law of thermodynamics. It would be impossible to extract energy as heat from a body at that temperature. Temperature is important in all fields of natur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
First Order
In mathematics and other formal sciences, first-order or first order most often means either: * "linear" (a polynomial of degree at most one), as in first-order approximation and other calculus uses, where it is contrasted with "polynomials of higher degree", or * "without self-reference", as in first-order logic and other logic uses, where it is contrasted with "allowing some self-reference" (higher-order logic) In detail, it may refer to: Mathematics * First-order approximation * First-order arithmetic * First-order condition * First-order hold, a mathematical model of the practical reconstruction of sampled signals * First-order inclusion probability * First Order Inductive Learner, a rule-based learning algorithm * First-order reduction, a very weak type of reduction between two computational problems * First-order resolution * First-order stochastic dominance * First order stream Differential equations * Exact first-order ordinary differential equation * First-order ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
