|
Finite Potential Barrier (QM)
In quantum mechanics, the rectangular (or, at times, square) potential barrier is a standard one-dimensional problem that demonstrates the phenomena of wave-mechanical tunneling (also called "quantum tunneling") and wave-mechanical reflection. The problem consists of solving the one-dimensional time-independent Schrödinger equation for a particle encountering a rectangular potential energy barrier. It is usually assumed, as here, that a free particle impinges on the barrier from the left. Although classically a particle behaving as a point mass would be reflected if its energy is less than a particle actually behaving as a matter wave has a non-zero probability of penetrating the barrier and continuing its travel as a wave on the other side. In classical wave-physics, this effect is known as evanescent wave coupling. The likelihood that the particle will pass through the barrier is given by the transmission coefficient, whereas the likelihood that it is reflected is given by ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square Potential
In quantum mechanics, the rectangular (or, at times, square) potential barrier is a standard one-dimensional problem that demonstrates the phenomena of wave-mechanical tunneling (also called "quantum tunneling") and wave-mechanical reflection. The problem consists of solving the one-dimensional time-independent Schrödinger equation for a particle encountering a rectangular potential energy barrier. It is usually assumed, as here, that a free particle impinges on the barrier from the left. Although classically a particle behaving as a point mass would be reflected if its energy is less than a particle actually behaving as a matter wave has a non-zero probability of penetrating the barrier and continuing its travel as a wave on the other side. In classical wave-physics, this effect is known as evanescent wave coupling. The likelihood that the particle will pass through the barrier is given by the transmission coefficient, whereas the likelihood that it is reflected is given by ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boundary Condition
In mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional constraints, called the boundary conditions. A solution to a boundary value problem is a solution to the differential equation which also satisfies the boundary conditions. Boundary value problems arise in several branches of physics as any physical differential equation will have them. Problems involving the wave equation, such as the determination of normal modes, are often stated as boundary value problems. A large class of important boundary value problems are the Sturm–Liouville problems. The analysis of these problems involves the eigenfunctions of a differential operator. To be useful in applications, a boundary value problem should be well posed. This means that given the input to the problem there exists a unique solution, which depends continuously on the input. Much theoretical work in the field of partial differential eq ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Models
In physics, a quantum (plural quanta) is the minimum amount of any physical entity ( physical property) involved in an interaction. The fundamental notion that a physical property can be "quantized" is referred to as "the hypothesis of quantization". This means that the magnitude of the physical property can take on only discrete values consisting of integer multiples of one quantum. For example, a photon is a single quantum of light (or of any other form of electromagnetic radiation). Similarly, the energy of an electron bound within an atom is quantized and can exist only in certain discrete values. (Atoms and matter in general are stable because electrons can exist only at discrete energy levels within an atom.) Quantization is one of the foundations of the much broader physics of quantum mechanics. Quantization of energy and its influence on how energy and matter interact (quantum electrodynamics) is part of the fundamental framework for understanding and describing nature. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pauli Exclusion Principle
In quantum mechanics, the Pauli exclusion principle states that two or more identical particles with half-integer spins (i.e. fermions) cannot occupy the same quantum state within a quantum system simultaneously. This principle was formulated by Austrian physicist Wolfgang Pauli in 1925 for electrons, and later extended to all fermions with his spin–statistics theorem of 1940. In the case of electrons in atoms, it can be stated as follows: it is impossible for two electrons of a poly-electron atom to have the same values of the four quantum numbers: ''n'', the principal quantum number; ', the azimuthal quantum number; ''m'', the magnetic quantum number; and ''ms'', the spin quantum number. For example, if two electrons reside in the same orbital, then their ''n'', ', and ''m'' values are the same; therefore their ''ms'' must be different, and thus the electrons must have opposite half-integer spin projections of 1/2 and −1/2. Particles with an integer spin, or bosons, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Finite Potential Well
The finite potential well (also known as the finite square well) is a concept from quantum mechanics. It is an extension of the infinite potential well, in which a particle is confined to a "box", but one which has finite potential "walls". Unlike the infinite potential well, there is a probability associated with the particle being found outside the box. The quantum mechanical interpretation is unlike the classical interpretation, where if the total energy of the particle is less than the potential energy barrier of the walls it cannot be found outside the box. In the quantum interpretation, there is a non-zero probability of the particle being outside the box even when the energy of the particle is less than the potential energy barrier of the walls (cf quantum tunnelling). Particle in a 1-dimensional box For the 1-dimensional case on the ''x''-axis, the time-independent Schrödinger equation can be written as: where *\hbar = \frac is the reduced Planck's constant, *h is Plan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Step Potential
Step(s) or STEP may refer to: Common meanings * Steps, making a staircase * Walking * Dance move * Military step, or march ** Marching Arts Films and television * ''Steps'' (TV series), Hong Kong * ''Step'' (film), US, 2017 Literature * ''Steps'' (novel), by Jerzy Kosinski * Systematic Training for Effective Parenting, a book series Music * Step (music), pitch change * Steps (pop group), UK * ''Step'' (Kara album), 2011, South Korea ** "Step" (Kara song) * ''Step'' (Meg album), 2007, Japan * "Step" (Vampire Weekend song) * "Step" (ClariS song) Organizations * Society of Trust and Estate Practitioners, international professional body for advisers who specialise in inheritance and succession planning * Board on Science, Technology, and Economic Policy of the U.S. National Academies * Solving the E-waste Problem, a UN organization Science, technology, and mathematics * Step (software), a physics simulator in KDE * Step function, in mathematics * Striatal-enriched prote ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Morse/Long-range Potential
The Morse/Long-range potential (MLR potential) is an interatomic interaction model for the potential energy of a diatomic molecule. Due to the simplicity of the regular Morse potential (it only has three adjustable parameters), it is very limited in its applicability in modern spectroscopy. The MLR potential is a modern version of the Morse potential which has the correct theoretical long-range form of the potential naturally built into it. It has been an important tool for spectroscopists to represent experimental data, verify measurements, and make predictions. It is useful for its extrapolation capability when data for certain regions of the potential are missing, its ability to predict energies with accuracy often better than the most sophisticated ''ab initio'' techniques, and its ability to determine precise empirical values for physical parameters such as the dissociation energy, equilibrium bond length, and long-range constants. Cases of particular note include: # the c- ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Delta Potential Barrier (QM)
In quantum mechanics the delta potential is a potential well mathematically described by the Dirac delta function - a generalized function. Qualitatively, it corresponds to a potential which is zero everywhere, except at a single point, where it takes an infinite value. This can be used to simulate situations where a particle is free to move in two regions of space with a barrier between the two regions. For example, an electron can move almost freely in a conducting material, but if two conducting surfaces are put close together, the interface between them acts as a barrier for the electron that can be approximated by a delta potential. The delta potential well is a limiting case of the finite potential well, which is obtained if one maintains the product of the width of the well and the potential constant while decreasing the well's width and increasing the potential. This article, for simplicity, only considers a one-dimensional potential well, but analysis could be expanded ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Separation Of Variables
In mathematics, separation of variables (also known as the Fourier method) is any of several methods for solving ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation. Ordinary differential equations (ODE) Suppose a differential equation can be written in the form :\frac f(x) = g(x)h(f(x)) which we can write more simply by letting y = f(x): :\frac=g(x)h(y). As long as ''h''(''y'') ≠ 0, we can rearrange terms to obtain: : = g(x) \, dx, so that the two variables ''x'' and ''y'' have been separated. ''dx'' (and ''dy'') can be viewed, at a simple level, as just a convenient notation, which provides a handy mnemonic aid for assisting with manipulations. A formal definition of ''dx'' as a differential (infinitesimal) is somewhat advanced. Alternative notation Those who dislike Leibniz's notation may prefer to write this as :\frac \frac = g(x), but that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scanning Tunneling Microscope
A scanning tunneling microscope (STM) is a type of microscope used for imaging surfaces at the atomic level. Its development in 1981 earned its inventors, Gerd Binnig and Heinrich Rohrer, then at IBM Zürich, the Nobel Prize in Physics in 1986. STM senses the surface by using an extremely sharp conducting tip that can distinguish features smaller than 0.1 nm with a 0.01 nm (10 pm) depth resolution. This means that individual atoms can routinely be imaged and manipulated. Most microscopes are built for use in ultra-high vacuum at temperatures approaching zero kelvin, but variants exist for studies in air, water and other environments, and for temperatures over 1000 °C. STM is based on the concept of quantum tunneling. When the tip is brought very near to the surface to be examined, a bias voltage applied between the two allows electrons to tunnel through the vacuum separating them. The resulting ''tunneling current'' is a function of the tip position, applied ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Effective Mass (solid-state Physics)
In solid state physics, a particle's effective mass (often denoted m^*) is the mass that it ''seems'' to have when responding to forces, or the mass that it seems to have when interacting with other identical particles in a thermal distribution. One of the results from the band theory of solids is that the movement of particles in a periodic potential, over long distances larger than the lattice spacing, can be very different from their motion in a vacuum. The effective mass is a quantity that is used to simplify band structures by modeling the behavior of a free particle with that mass. For some purposes and some materials, the effective mass can be considered to be a simple constant of a material. In general, however, the value of effective mass depends on the purpose for which it is used, and can vary depending on a number of factors. For electrons or electron holes in a solid, the effective mass is usually stated as a factor multiplying the rest mass of an electron, ''m'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
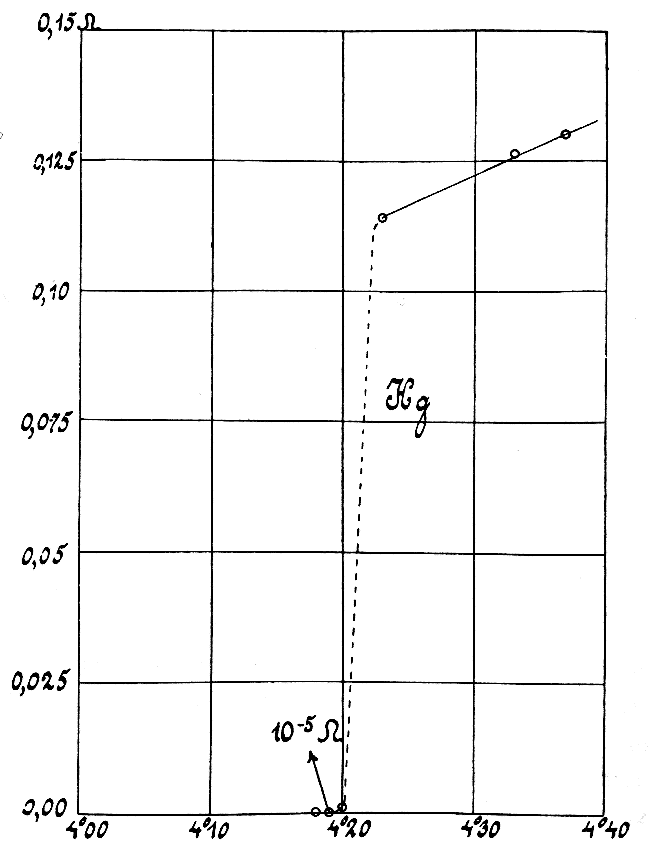
Electrical Conductivity
Electrical resistivity (also called specific electrical resistance or volume resistivity) is a fundamental property of a material that measures how strongly it resists electric current. A low resistivity indicates a material that readily allows electric current. Resistivity is commonly represented by the Greek letter (rho). The SI unit of electrical resistivity is the ohm-meter (Ω⋅m). For example, if a solid cube of material has sheet contacts on two opposite faces, and the resistance between these contacts is , then the resistivity of the material is . Electrical conductivity or specific conductance is the reciprocal of electrical resistivity. It represents a material's ability to conduct electric current. It is commonly signified by the Greek letter ( sigma), but ( kappa) (especially in electrical engineering) and ( gamma) are sometimes used. The SI unit of electrical conductivity is siemens per metre (S/m). Resistivity and conductivity are inte ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |