|
Final Value Theorem
In mathematical analysis, the final value theorem (FVT) is one of several similar theorems used to relate frequency domain expressions to the time domain behavior as time approaches infinity. Mathematically, if f(t) in continuous time has (unilateral) Laplace transform F(s), then a final value theorem establishes conditions under which \lim_f(t) = \lim_. Likewise, if f /math> in discrete time has (unilateral) Z-transform F(z), then a final value theorem establishes conditions under which \lim_f = \lim_. An Abelian final value theorem makes assumptions about the time-domain behavior of f(t) \textf to calculate \lim_. Conversely, a Tauberian final value theorem makes assumptions about the frequency-domain behaviour of F(s) to calculate \lim_f(t) \text\lim_f (see Abelian and Tauberian theorems for integral transforms). Final value theorems for the Laplace transform Deducing In the following statements, the notation \texts \to 0\text means that s approaches 0, whereas \text ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Analysis
Analysis is the branch of mathematics dealing with continuous functions, limit (mathematics), limits, and related theories, such as Derivative, differentiation, Integral, integration, measure (mathematics), measure, infinite sequences, series (mathematics), series, and analytic functions. These theories are usually studied in the context of Real number, real and Complex number, complex numbers and Function (mathematics), functions. Analysis evolved from calculus, which involves the elementary concepts and techniques of analysis. Analysis may be distinguished from geometry; however, it can be applied to any Space (mathematics), space of mathematical objects that has a definition of nearness (a topological space) or specific distances between objects (a metric space). History Ancient Mathematical analysis formally developed in the 17th century during the Scientific Revolution, but many of its ideas can be traced back to earlier mathematicians. Early results in analysis were ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dirichlet Integral
In mathematics, there are several integrals known as the Dirichlet integral, after the German mathematician Peter Gustav Lejeune Dirichlet, one of which is the improper integral of the sinc function over the positive real number line. \int_0^\infty \frac \,dx = \frac. This integral is not absolutely convergent, meaning \left, \frac \ has infinite Lebesgue or Riemann improper integrals over the positive real line, so the sinc function is not Lebesgue integrable over the positive real line. The sinc function is, however, integrable in the sense of the improper Riemann integral or the generalized Riemann or Henstock–Kurzweil integral. This can be seen by using Dirichlet's test for improper integrals. It is a good illustration of special techniques for evaluating definite integrals, particularly when it is not useful to directly apply the fundamental theorem of calculus due to the lack of an elementary antiderivative for the integrand, as the sine integral, an antideriva ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Laplace Transform
In mathematics, the Laplace transform, named after Pierre-Simon Laplace (), is an integral transform that converts a Function (mathematics), function of a Real number, real Variable (mathematics), variable (usually t, in the ''time domain'') to a function of a Complex number, complex variable s (in the complex-valued frequency domain, also known as ''s''-domain, or ''s''-plane). The transform is useful for converting derivative, differentiation and integral, integration in the time domain into much easier multiplication and Division (mathematics), division in the Laplace domain (analogous to how logarithms are useful for simplifying multiplication and division into addition and subtraction). This gives the transform many applications in science and engineering, mostly as a tool for solving linear differential equations and dynamical systems by simplifying ordinary differential equations and integral equations into algebraic equation, algebraic polynomial equations, and by simplifyin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Initial Value Theorem
In mathematical analysis, the initial value theorem is a theorem used to relate frequency domain expressions to the time domain behavior as time approaches zero. Let : F(s) = \int_0^\infty f(t) e^\,dt be the (one-sided) Laplace transform of ''ƒ''(''t''). If f is bounded on (0,\infty) (or if just f(t)=O(e^)) and \lim_f(t) exists then the initial value theorem saysRobert H. Cannon, ''Dynamics of Physical Systems'', Courier Dover Publications, 2003, page 567. : \lim_f(t)=\lim_. Proofs Proof using dominated convergence theorem and assuming that function is bounded Suppose first that f is bounded, i.e. \lim_f(t)=\alpha. A change of variable in the integral \int_0^\infty f(t)e^\,dt shows that :sF(s)=\int_0^\infty f\left(\frac ts\right)e^\,dt. Since f is bounded, the Dominated Convergence Theorem In measure theory, Lebesgue's dominated convergence theorem gives a mild sufficient condition under which limits and integrals of a sequence of functions can be interchange ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Control Theory
Control theory is a field of control engineering and applied mathematics that deals with the control system, control of dynamical systems in engineered processes and machines. The objective is to develop a model or algorithm governing the application of system inputs to drive the system to a desired state, while minimizing any ''delay'', ''overshoot'', or ''steady-state error'' and ensuring a level of control Stability theory, stability; often with the aim to achieve a degree of Optimal control, optimality. To do this, a controller with the requisite corrective behavior is required. This controller monitors the controlled process variable (PV), and compares it with the reference or Setpoint (control system), set point (SP). The difference between actual and desired value of the process variable, called the ''error'' signal, or SP-PV error, is applied as feedback to generate a control action to bring the controlled process variable to the same value as the set point. Other aspects ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
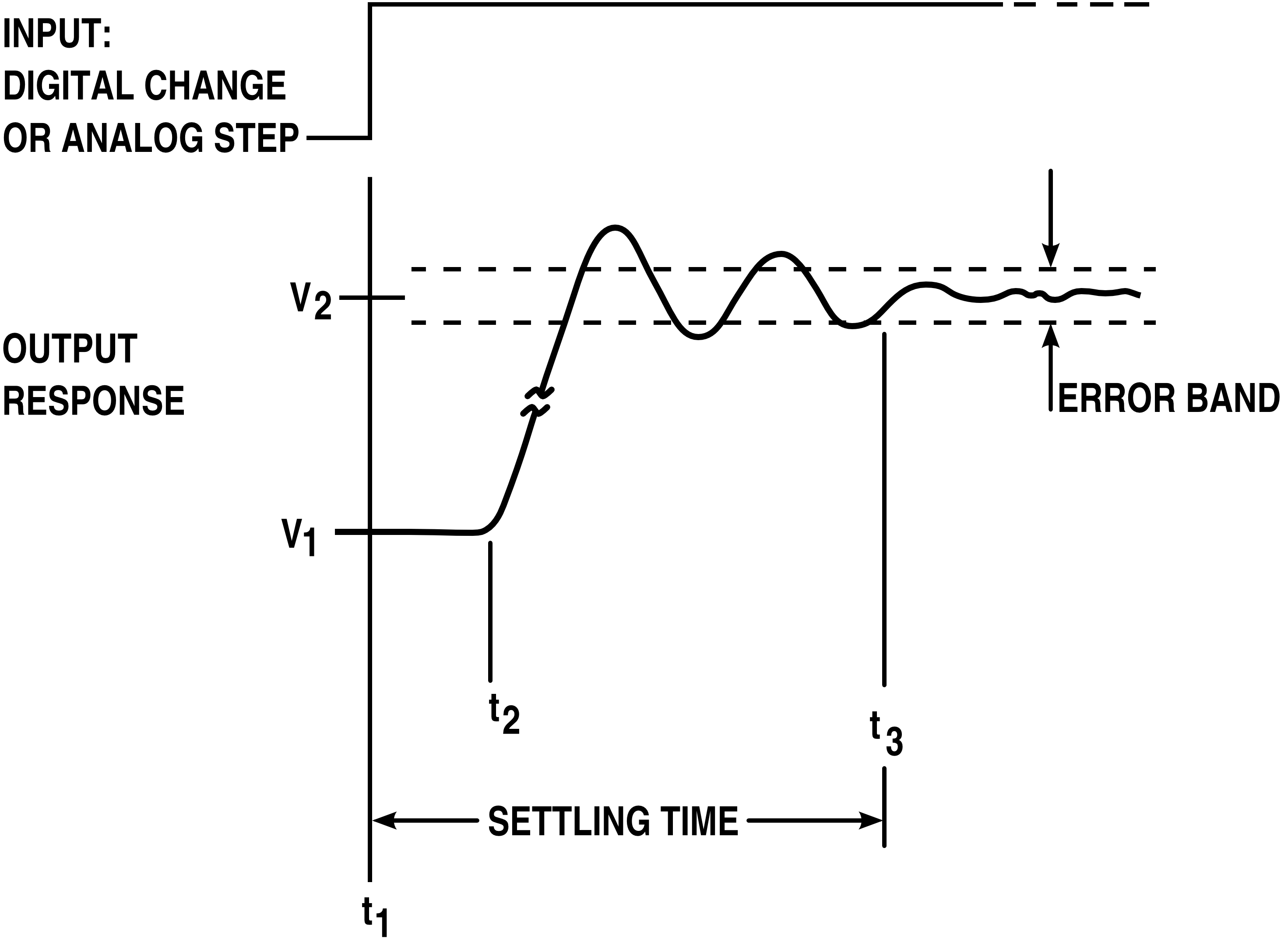
Step Response
The step response of a system in a given initial state consists of the time evolution of its outputs when its control inputs are Heaviside step functions. In electronic engineering and control theory, step response is the time behaviour of the outputs of a general system when its inputs change from zero to one in a very short time. The concept can be extended to the abstract mathematical notion of a dynamical system using an evolution parameter. From a practical standpoint, knowing how the system responds to a sudden input is important because large and possibly fast deviations from the long term steady state may have extreme effects on the component itself and on other portions of the overall system dependent on this component. In addition, the overall system cannot act until the component's output settles down to some vicinity of its final state, delaying the overall system response. Formally, knowing the step response of a dynamical system gives information on the stability of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Impulse Response
In signal processing and control theory, the impulse response, or impulse response function (IRF), of a dynamic system is its output when presented with a brief input signal, called an impulse (). More generally, an impulse response is the reaction of any dynamic system in response to some external change. In both cases, the impulse response describes the reaction of the system as a function of time (or possibly as a function of some other independent variable that parameterizes the dynamic behavior of the system). In all these cases, the dynamic system and its impulse response may be actual physical objects, or may be mathematical systems of equations describing such objects. Since the impulse function contains all frequencies (see the Fourier transform of the Dirac delta function, showing infinite frequency bandwidth that the Dirac delta function has), the impulse response defines the response of a linear time-invariant system for all frequencies. Mathematical considerat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Transfer Function
In engineering, a transfer function (also known as system function or network function) of a system, sub-system, or component is a function (mathematics), mathematical function that mathematical model, models the system's output for each possible input. It is widely used in electronic engineering tools like Electronic circuit simulation, circuit simulators and control systems. In simple cases, this function can be represented as a two-dimensional graph (function), graph of an independent scalar (mathematics), scalar input versus the dependent scalar output (known as a transfer curve or characteristic curve). Transfer functions for components are used to design and analyze systems assembled from components, particularly using the block diagram technique, in electronics and control theory. Dimensions and units of the transfer function model the output response of the device for a range of possible inputs. The transfer function of a two-port electronic circuit, such as an amplifier, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inverse Laplace Transform
In mathematics, the inverse Laplace transform of a function F(s) is a real function f(t) that is piecewise- continuous, exponentially-restricted (that is, , f(t), \leq Me^ \forall t \geq 0 for some constants M > 0 and \alpha \in \mathbb) and has the property: :\mathcal\(s) = \mathcal\(s) = F(s), where \mathcal denotes the Laplace transform. It can be proven that, if a function F(s) has the inverse Laplace transform f(t), then f(t) is uniquely determined (considering functions which differ from each other only on a point set having Lebesgue measure zero as the same). This result was first proven by Mathias Lerch in 1903 and is known as Lerch's theorem. The Laplace transform and the inverse Laplace transform together have a number of properties that make them useful for analysing linear dynamical systems. Mellin's inverse formula An integral formula for the inverse Laplace transform, called the ''Mellin's inverse formula'', the '' Bromwich integral'', or the '' Fourier– Me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Laplace–Stieltjes Transform
The Laplace–Stieltjes transform, named for Pierre-Simon Laplace and Thomas Joannes Stieltjes, is an integral transform similar to the Laplace transform. For real-valued functions, it is the Laplace transform of a Stieltjes measure, however it is often defined for functions with values in a Banach space. It is useful in a number of areas of mathematics, including functional analysis, and certain areas of theoretical and applied probability. Real-valued functions The Laplace–Stieltjes transform of a real-valued function ''g'' is given by a Lebesgue–Stieltjes integral of the form :\int e^\,dg(x) for ''s'' a complex number. As with the usual Laplace transform, one gets a slightly different transform depending on the domain of integration, and for the integral to be defined, one also needs to require that ''g'' be of bounded variation on the region of integration. The most common are: * The bilateral (or two-sided) Laplace–Stieltjes transform is given by \(s) = \int_^ e^\,dg( ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Moment (mathematics)
In mathematics, the moments of a function are certain quantitative measures related to the shape of the function's graph. If the function represents mass density, then the zeroth moment is the total mass, the first moment (normalized by total mass) is the center of mass, and the second moment is the moment of inertia. If the function is a probability distribution, then the first moment is the expected value, the second central moment is the variance, the third standardized moment is the skewness, and the fourth standardized moment is the kurtosis. For a distribution of mass or probability on a bounded interval, the collection of all the moments (of all orders, from to ) uniquely determines the distribution ( Hausdorff moment problem). The same is not true on unbounded intervals ( Hamburger moment problem). In the mid-nineteenth century, Pafnuty Chebyshev became the first person to think systematically in terms of the moments of random variables. Significance of th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dirichlet's Test
In mathematics, Dirichlet's test is a method of testing for the convergence of a series that is especially useful for proving conditional convergence. It is named after its author Peter Gustav Lejeune Dirichlet, and was published posthumously in the '' Journal de Mathématiques Pures et Appliquées'' in 1862. Statement The test states that if (a_n) is a monotonic sequence of real numbers with \lim_ a_n = 0 and (b_n) is a sequence of real numbers or complex numbers with bounded partial sums, then the series :\sum_^ a_n b_n converges. Proof Let S_n = \sum_^n a_k b_k and B_n = \sum_^n b_k. From summation by parts, we have that S_n = a_ B_n + \sum_^ B_k (a_k - a_). Since the magnitudes of the partial sums B_n are bounded by some ''M'' and a_n \to 0 as n\to\infty, the first of these terms approaches zero: , a_ B_n, \leq , a_ M, \to 0 as n\to\infty. Furthermore, for each ''k'', , B_k (a_k - a_), \leq M, a_k - a_, . Since (a_n) is monotone, it is either decreasing or in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |