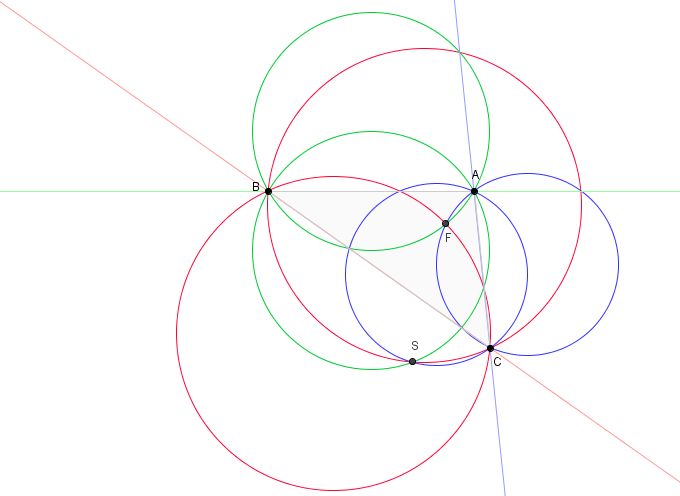
|
Fermat Point
In Euclidean geometry, the Fermat point of a triangle, also called the Torricelli point or Fermat–Torricelli point, is a point such that the sum of the three distances from each of the three vertices of the triangle to the point is the smallest possible. It is so named because this problem was first raised by Fermat in a private letter to Evangelista Torricelli, who solved it. The Fermat point gives a solution to the geometric median and Steiner tree problems for three points. Construction The Fermat point of a triangle with largest angle at most 120° is simply its first isogonic center or X(13), which is constructed as follows: # Construct an equilateral triangle on each of two arbitrarily chosen sides of the given triangle. # Draw a line from each new vertex to the opposite vertex of the original triangle. # The two lines intersect at the Fermat point. An alternative method is the following: # On each of two arbitrarily chosen sides, construct an isosceles triangle, with ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fermat Point
In Euclidean geometry, the Fermat point of a triangle, also called the Torricelli point or Fermat–Torricelli point, is a point such that the sum of the three distances from each of the three vertices of the triangle to the point is the smallest possible. It is so named because this problem was first raised by Fermat in a private letter to Evangelista Torricelli, who solved it. The Fermat point gives a solution to the geometric median and Steiner tree problems for three points. Construction The Fermat point of a triangle with largest angle at most 120° is simply its first isogonic center or X(13), which is constructed as follows: # Construct an equilateral triangle on each of two arbitrarily chosen sides of the given triangle. # Draw a line from each new vertex to the opposite vertex of the original triangle. # The two lines intersect at the Fermat point. An alternative method is the following: # On each of two arbitrarily chosen sides, construct an isosceles triangle, with ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triangle Inequality
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side. This statement permits the inclusion of degenerate triangles, but some authors, especially those writing about elementary geometry, will exclude this possibility, thus leaving out the possibility of equality. If , , and are the lengths of the sides of the triangle, with no side being greater than , then the triangle inequality states that :z \leq x + y , with equality only in the degenerate case of a triangle with zero area. In Euclidean geometry and some other geometries, the triangle inequality is a theorem about distances, and it is written using vectors and vector lengths ( norms): :\, \mathbf x + \mathbf y\, \leq \, \mathbf x\, + \, \mathbf y\, , where the length of the third side has been replaced by the vector sum . When and are real numbers, they can be viewed as vectors in , and the trian ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nine-point Circle
In geometry, the nine-point circle is a circle that can be constructed for any given triangle. It is so named because it passes through nine significant concyclic points defined from the triangle. These nine points are: * The midpoint of each side of the triangle * The foot of each altitude * The midpoint of the line segment from each vertex of the triangle to the orthocenter (where the three altitudes meet; these line segments lie on their respective altitudes). The nine-point circle is also known as Feuerbach's circle (after Karl Wilhelm Feuerbach), Euler's circle (after Leonhard Euler), Terquem's circle (after Olry Terquem), the six-points circle, the twelve-points circle, the -point circle, the medioscribed circle, the mid circle or the circum-midcircle. Its center is the nine-point center of the triangle. Nine significant points The diagram above shows the nine significant points of the nine-point circle. Points are the midpoints of the three sides of the triangle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euler Line
In geometry, the Euler line, named after Leonhard Euler (), is a line determined from any triangle that is not equilateral. It is a central line of the triangle, and it passes through several important points determined from the triangle, including the orthocenter, the circumcenter, the centroid, the Exeter point and the center of the nine-point circle of the triangle. The concept of a triangle's Euler line extends to the Euler line of other shapes, such as the quadrilateral and the tetrahedron. Triangle centers on the Euler line Individual centers Euler showed in 1765 that in any triangle, the orthocenter, circumcenter and centroid are collinear. This property is also true for another triangle center, the nine-point center, although it had not been defined in Euler's time. In equilateral triangles, these four points coincide, but in any other triangle they are all distinct from each other, and the Euler line is determined by any two of them. Other notable points that lie on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circumcevian Triangle
In triangle geometry, a circumcevian triangle is a special triangle associated with the reference triangle and a point in the plane of the triangle. It is also associated with the circumcircle of the reference triangle. Definition Let P be a point in the plane of the reference triangle ABC. Let the lines AP, BP, CP intersect the circumcircle of triangle ABC at A', B', C'. The triangle A'B'C' is called the circumcevian triangle of P with reference to the triangle ABC. Coordinates Let a,b,c be the side lengths of triangle ABC and let the trilinear coordinates of P be \alpha:\beta:\gamma. Then the trilinear coordinates of the vertices of the circumcevian triangle of P are as follows: :A' (-a\beta\gamma : (b\gamma+c\beta)\beta : (b\gamma+c\beta)\gamma) :B' ((c\alpha +a\gamma)\alpha : - b\gamma\alpha : (c\alpha +a\gamma) \gamma) :C' ((a\beta +b\alpha)\alpha : (a\beta +b\alpha)\beta : - c\alpha\beta) Some properties *Every triangle inscribed in the circumcircle of the reference triangle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pedal Triangle
In geometry, a pedal triangle is obtained by projecting a point onto the sides of a triangle. More specifically, consider a triangle ''ABC'', and a point ''P'' that is not one of the vertices ''A, B, C''. Drop perpendiculars from ''P'' to the three sides of the triangle (these may need to be produced, i.e., extended). Label ''L'', ''M'', ''N'' the intersections of the lines from ''P'' with the sides ''BC'', ''AC'', ''AB''. The pedal triangle is then ''LMN''. If ABC is not an obtuse triangle, P is the orthocenter then the angles of LMN are 180°−2A, 180°−2B and 180°−2C. The location of the chosen point ''P'' relative to the chosen triangle ''ABC'' gives rise to some special cases: * If ''P = ''orthocenter, then ''LMN = '' orthic triangle. * If ''P = ''incenter, then ''LMN = ''intouch triangle. * If ''P = ''circumcenter, then ''LMN = ''medial triangle. If ''P'' is on the circumcircle of the triangle, ''LMN'' collapses to a line. This is then called the pedal line, or so ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isodynamic Point
In Euclidean geometry, the isodynamic points of a triangle are points associated with the triangle, with the properties that an inversion centered at one of these points transforms the given triangle into an equilateral triangle, and that the distances from the isodynamic point to the triangle vertices are inversely proportional to the opposite side lengths of the triangle. Triangles that are similar to each other have isodynamic points in corresponding locations in the plane, so the isodynamic points are triangle centers, and unlike other triangle centers the isodynamic points are also invariant under Möbius transformations. A triangle that is itself equilateral has a unique isodynamic point, at its centroid(as well as its orthocenter, its incenter, and its circumcenter, which are concurrent); every non-equilateral triangle has two isodynamic points. Isodynamic points were first studied and named by . Distance ratios The isodynamic points were originally defined from certain eq ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boolean Domain
In mathematics and abstract algebra, a Boolean domain is a set consisting of exactly two elements whose interpretations include ''false'' and ''true''. In logic, mathematics and theoretical computer science, a Boolean domain is usually written as , or \mathbb. The algebraic structure that naturally builds on a Boolean domain is the Boolean algebra with two elements. The initial object in the category of bounded lattices is a Boolean domain. In computer science, a Boolean variable is a variable that takes values in some Boolean domain. Some programming languages feature reserved words or symbols for the elements of the Boolean domain, for example false and true. However, many programming languages do not have a Boolean datatype in the strict sense. In C or BASIC, for example, falsity is represented by the number 0 and truth is represented by the number 1 or −1, and all variables that can take these values can also take any other numerical values. Generalizations The Boole ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trilinear Coordinates
In geometry, the trilinear coordinates of a point relative to a given triangle describe the relative directed distances from the three sidelines of the triangle. Trilinear coordinates are an example of homogeneous coordinates. The ratio is the ratio of the perpendicular distances from the point to the sides (extended if necessary) opposite vertices and respectively; the ratio is the ratio of the perpendicular distances from the point to the sidelines opposite vertices and respectively; and likewise for and vertices and . In the diagram at right, the trilinear coordinates of the indicated interior point are the actual distances (, , ), or equivalently in ratio form, for any positive constant . If a point is on a sideline of the reference triangle, its corresponding trilinear coordinate is 0. If an exterior point is on the opposite side of a sideline from the interior of the triangle, its trilinear coordinate associated with that sideline is negative. It is impossible ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circumcircle
In geometry, the circumscribed circle or circumcircle of a polygon is a circle that passes through all the vertices of the polygon. The center of this circle is called the circumcenter and its radius is called the circumradius. Not every polygon has a circumscribed circle. A polygon that does have one is called a cyclic polygon, or sometimes a concyclic polygon because its vertices are concyclic. All triangles, all regular simple polygons, all rectangles, all isosceles trapezoids, and all right kites are cyclic. A related notion is the one of a minimum bounding circle, which is the smallest circle that completely contains the polygon within it, if the circle's center is within the polygon. Every polygon has a unique minimum bounding circle, which may be constructed by a linear time algorithm. Even if a polygon has a circumscribed circle, it may be different from its minimum bounding circle. For example, for an obtuse triangle, the minimum bounding circle has the longest sid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Law Of Cosines
In trigonometry, the law of cosines (also known as the cosine formula, cosine rule, or al-Kashi's theorem) relates the lengths of the sides of a triangle to the cosine of one of its angles. Using notation as in Fig. 1, the law of cosines states :c^2 = a^2 + b^2 - 2ab\cos\gamma, where denotes the angle contained between sides of lengths and and opposite the side of length . For the same figure, the other two relations are analogous: :a^2=b^2+c^2-2bc\cos\alpha, :b^2=a^2+c^2-2ac\cos\beta. The law of cosines generalizes the Pythagorean theorem, which holds only for right triangles: if the angle is a right angle (of measure 90 degrees, or radians), then , and thus the law of cosines reduces to the Pythagorean theorem: :c^2 = a^2 + b^2. The law of cosines is useful for computing the third side of a triangle when two sides and their enclosed angle are known. History Though the notion of the cosine was not yet developed in his time, Euclid's '' Elements'', dating back to th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
