|
Fermat's Conjecture
In number theory, Fermat's Last Theorem (sometimes called Fermat's conjecture, especially in older texts) states that no three positive integers , , and satisfy the equation for any integer value of greater than 2. The cases and have been known since antiquity to have infinitely many solutions.Singh, pp. 18–20. The proposition was first stated as a theorem by Pierre de Fermat around 1637 in the margin of a copy of ''Arithmetica''. Fermat added that he had a proof that was too large to fit in the margin. Although other statements claimed by Fermat without proof were subsequently proven by others and credited as theorems of Fermat (for example, Fermat's theorem on sums of two squares), Fermat's Last Theorem resisted proof, leading to doubt that Fermat ever had a correct proof. Consequently the proposition became known as a conjecture rather than a theorem. After 358 years of effort by mathematicians, the first successful proof was released in 1994 by Andrew Wiles and form ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diophantus
Diophantus of Alexandria ( grc, Διόφαντος ὁ Ἀλεξανδρεύς; born probably sometime between AD 200 and 214; died around the age of 84, probably sometime between AD 284 and 298) was an Alexandrian mathematician, who was the author of a series of books called '' Arithmetica'', many of which are now lost. His texts deal with solving algebraic equations. Diophantine equations ("Diophantine geometry") and Diophantine approximations are important areas of mathematical research. Diophantus coined the term παρισότης (parisotes) to refer to an approximate equality. This term was rendered as ''adaequalitas'' in Latin, and became the technique of adequality developed by Pierre de Fermat to find maxima for functions and tangent lines to curves. Diophantus was the first Greek mathematician who recognized fractions as numbers; thus he allowed positive rational numbers for the coefficients and solutions. In modern use, Diophantine equations are usually algebraic equ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Modularity Theorem
The modularity theorem (formerly called the Taniyama–Shimura conjecture, Taniyama-Weil conjecture or modularity conjecture for elliptic curves) states that elliptic curves over the field of rational numbers are related to modular forms. Andrew Wiles proved the modularity theorem for semistable elliptic curves, which was enough to imply Fermat's Last Theorem. Later, a series of papers by Wiles's former students Brian Conrad, Fred Diamond and Richard Taylor, culminating in a joint paper with Christophe Breuil, extended Wiles's techniques to prove the full modularity theorem in 2001. Statement The theorem states that any elliptic curve over \mathbf can be obtained via a rational map with integer coefficients from the classical modular curve X_0(N) for some integer N; this is a curve with integer coefficients with an explicit definition. This mapping is called a modular parametrization of level N. If N is the smallest integer for which such a parametrization can be found (wh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regular Prime
In number theory, a regular prime is a special kind of prime number, defined by Ernst Kummer in 1850 to prove certain cases of Fermat's Last Theorem. Regular primes may be defined via the divisibility of either class numbers or of Bernoulli numbers. The first few regular odd primes are: : 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 41, 43, 47, 53, 61, 71, 73, 79, 83, 89, 97, 107, 109, 113, 127, 137, 139, 151, 163, 167, 173, 179, 181, 191, 193, 197, 199, ... . History and motivation In 1850, Kummer proved that Fermat's Last Theorem is true for a prime exponent ''p'' if ''p'' is regular. This focused attention on the irregular primes. In 1852, Genocchi was able to prove that the first case of Fermat's Last Theorem is true for an exponent ''p'', if is not an irregular pair. Kummer improved this further in 1857 by showing that for the "first case" of Fermat's Last Theorem (see Sophie Germain's theorem) it is sufficient to establish that either or fails to be an irregular pair. Kummer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ernst Kummer
Ernst Eduard Kummer (29 January 1810 – 14 May 1893) was a German mathematician. Skilled in applied mathematics, Kummer trained German army officers in ballistics; afterwards, he taught for 10 years in a '' gymnasium'', the German equivalent of high school, where he inspired the mathematical career of Leopold Kronecker. Life Kummer was born in Sorau, Brandenburg (then part of Prussia). He was awarded a PhD from the University of Halle in 1831 for writing a prize-winning mathematical essay (''De cosinuum et sinuum potestatibus secundum cosinus et sinus arcuum multiplicium evolvendis''), which was eventually published a year later. In 1840, Kummer married Ottilie Mendelssohn, daughter of Nathan Mendelssohn and Henriette Itzig. Ottilie was a cousin of Felix Mendelssohn and his sister Rebecca Mendelssohn Bartholdy, the wife of the mathematician Peter Gustav Lejeune Dirichlet. His second wife (whom he married soon after the death of Ottilie in 1848), Bertha Cauer, was a maternal co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sophie Germain
Marie-Sophie Germain (; 1 April 1776 – 27 June 1831) was a French mathematician, physicist, and philosopher. Despite initial opposition from her parents and difficulties presented by society, she gained education from books in her father's library, including ones by Euler, and from correspondence with famous mathematicians such as Lagrange, Legendre, and Gauss (under the pseudonym of Monsieur LeBlanc). One of the pioneers of elasticity theory, she won the grand prize from the Paris Academy of Sciences for her essay on the subject. Her work on Fermat's Last Theorem provided a foundation for mathematicians exploring the subject for hundreds of years after. Because of prejudice against her sex, she was unable to make a career out of mathematics, but she worked independently throughout her life. Before her death, Gauss had recommended that she be awarded an honorary degree, but that never occurred. On 27 June 1831, she died from breast cancer. At the centenary of her life, a stre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prime Number
A prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways of writing it as a product, or , involve 5 itself. However, 4 is composite because it is a product (2 × 2) in which both numbers are smaller than 4. Primes are central in number theory because of the fundamental theorem of arithmetic: every natural number greater than 1 is either a prime itself or can be factorized as a product of primes that is unique up to their order. The property of being prime is called primality. A simple but slow method of checking the primality of a given number n, called trial division, tests whether n is a multiple of any integer between 2 and \sqrt. Faster algorithms include the Miller–Rabin primality test, which is fast but has a small chance of error, and the AKS primality test, which always pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exponent
Exponentiation is a mathematical operation, written as , involving two numbers, the '' base'' and the ''exponent'' or ''power'' , and pronounced as " (raised) to the (power of) ". When is a positive integer, exponentiation corresponds to repeated multiplication of the base: that is, is the product of multiplying bases: b^n = \underbrace_. The exponent is usually shown as a superscript to the right of the base. In that case, is called "''b'' raised to the ''n''th power", "''b'' (raised) to the power of ''n''", "the ''n''th power of ''b''", "''b'' to the ''n''th power", or most briefly as "''b'' to the ''n''th". Starting from the basic fact stated above that, for any positive integer n, b^n is n occurrences of b all multiplied by each other, several other properties of exponentiation directly follow. In particular: \begin b^ & = \underbrace_ \\ ex& = \underbrace_ \times \underbrace_ \\ ex& = b^n \times b^m \end In other words, when multiplying a base raised to one exp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Unsolved Problems In Mathematics
Many mathematical problems have been stated but not yet solved. These problems come from many areas of mathematics, such as theoretical physics, computer science, algebra, analysis, combinatorics, algebraic, differential, discrete and Euclidean geometries, graph theory, group theory, model theory, number theory, set theory, Ramsey theory, dynamical systems, and partial differential equations. Some problems belong to more than one discipline and are studied using techniques from different areas. Prizes are often awarded for the solution to a long-standing problem, and some lists of unsolved problems, such as the Millennium Prize Problems, receive considerable attention. This list is a composite of notable unsolved problems mentioned in previously published lists, including but not limited to lists considered authoritative. Although this list may never be comprehensive, the problems listed here vary widely in both difficulty and importance. Lists of unsolved problems in math ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Proof
A mathematical proof is an inferential argument for a mathematical statement, showing that the stated assumptions logically guarantee the conclusion. The argument may use other previously established statements, such as theorems; but every proof can, in principle, be constructed using only certain basic or original assumptions known as axioms, along with the accepted rules of inference. Proofs are examples of exhaustive deductive reasoning which establish logical certainty, to be distinguished from empirical arguments or non-exhaustive inductive reasoning which establish "reasonable expectation". Presenting many cases in which the statement holds is not enough for a proof, which must demonstrate that the statement is true in ''all'' possible cases. A proposition that has not been proved but is believed to be true is known as a conjecture, or a hypothesis if frequently used as an assumption for further mathematical work. Proofs employ logic expressed in mathematical symbols ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pythagorean Triple
A Pythagorean triple consists of three positive integers , , and , such that . Such a triple is commonly written , and a well-known example is . If is a Pythagorean triple, then so is for any positive integer . A primitive Pythagorean triple is one in which , and are coprime (that is, they have no common divisor larger than 1). For example, is a primitive Pythagorean triple whereas is not. A triangle whose sides form a Pythagorean triple is called a Pythagorean triangle, and is necessarily a right triangle. The name is derived from the Pythagorean theorem, stating that every right triangle has side lengths satisfying the formula a^2+b^2=c^2; thus, Pythagorean triples describe the three integer side lengths of a right triangle. However, right triangles with non-integer sides do not form Pythagorean triples. For instance, the triangle with sides a=b=1 and c=\sqrt2 is a right triangle, but (1,1,\sqrt2) is not a Pythagorean triple because \sqrt2 is not an integer. Moreover, 1 and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pythagorean Theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite the right angle) is equal to the sum of the areas of the squares on the other two sides. This theorem can be written as an equation relating the lengths of the sides ''a'', ''b'' and the hypotenuse ''c'', often called the Pythagorean equation: :a^2 + b^2 = c^2 , The theorem is named for the Greek philosopher Pythagoras, born around 570 BC. The theorem has been proven numerous times by many different methods – possibly the most for any mathematical theorem. The proofs are diverse, including both geometric proofs and algebraic proofs, with some dating back thousands of years. When Euclidean space is represented by a Cartesian coordinate system in analytic geometry, Euclidean distance satisfies the Pythagorean relation: the squared dist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Guinness Book Of World Records
''Guinness World Records'', known from its inception in 1955 until 1999 as ''The Guinness Book of Records'' and in previous United States editions as ''The Guinness Book of World Records'', is a reference book published annually, listing world records both of human achievements and the extremes of the natural world. The brainchild of Sir Hugh Beaver, the book was co-founded by twin brothers Norris and Ross McWhirter in Fleet Street, London, in August 1955. The first edition topped the best-seller list in the United Kingdom by Christmas 1955. The following year the book was launched internationally, and as of the 2022 edition, it is now in its 67th year of publication, published in 100 countries and 23 languages, and maintains over 53,000 records in its database. The international franchise has extended beyond print to include television series and museums. The popularity of the franchise has resulted in ''Guinness World Records'' becoming the primary international authority ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |


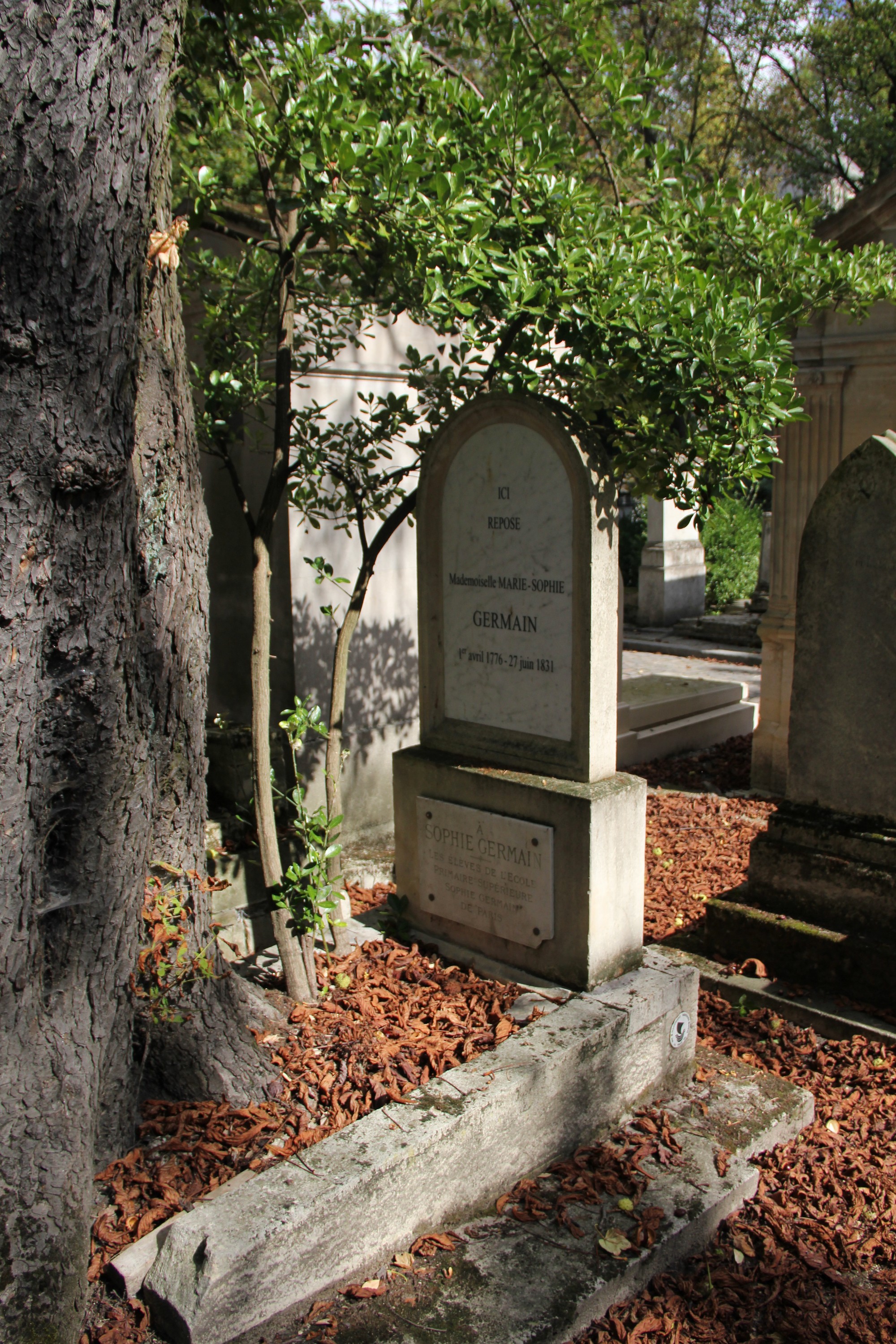




.jpg)