|
Fano Factor
In statistics, the Fano factor, like the coefficient of variation, is a measure of the statistical dispersion, dispersion of a counting process. It was originally used to measure the Fano noise in ion detectors. It is named after Ugo Fano, an Italian-American physicist. The Fano factor after a time t is defined as :F(t)=\frac, where \sigma_t is the standard deviation and \mu_t is the mean number of events of a counting process after some time t. The Fano factor can be viewed as a kind of noise-to-signal ratio; it is a measure of the reliability with which the waiting time random variable can be estimated after several random events. For a Poisson point process, Poisson counting process, the variance in the count equals the mean count, so F=1. Definition For a counting process N_t, the Fano factor after a time t>0 is defined as, :F(t)=\frac. Sometimes, the long-term limit is also termed the Fano factor, :F=\lim_F(t). For a renewal process with holding times distributed s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German language, German: ', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of statistical survey, surveys and experimental design, experiments. When census data (comprising every member of the target population) cannot be collected, statisticians collect data by developing specific experiment designs and survey sample (statistics), samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coefficient Of Variation
In probability theory and statistics, the coefficient of variation (CV), also known as normalized root-mean-square deviation (NRMSD), percent RMS, and relative standard deviation (RSD), is a standardized measure of dispersion of a probability distribution or frequency distribution. It is defined as the ratio of the standard deviation \sigma to the mean \mu (or its absolute value, , and often expressed as a percentage ("%RSD"). The CV or RSD is widely used in analytical chemistry to express the precision and repeatability of an assay. It is also commonly used in fields such as engineering or physics when doing quality assurance studies and ANOVA gauge R&R, by economists and investors in economic models, in epidemiology, and in psychology/neuroscience. Definition The coefficient of variation (CV) is defined as the ratio of the standard deviation \sigma to the mean \mu, CV = \frac. It shows the extent of variability in relation to the mean of the population. The coefficien ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Dispersion
In statistics, dispersion (also called variability, scatter, or spread) is the extent to which a distribution is stretched or squeezed. Common examples of measures of statistical dispersion are the variance, standard deviation, and interquartile range. For instance, when the variance of data in a set is large, the data is widely scattered. On the other hand, when the variance is small, the data in the set is clustered. Dispersion is contrasted with location or central tendency, and together they are the most used properties of distributions. Measures of statistical dispersion A measure of statistical dispersion is a nonnegative real number that is zero if all the data are the same and increases as the data become more diverse. Most measures of dispersion have the same units as the quantity being measured. In other words, if the measurements are in metres or seconds, so is the measure of dispersion. Examples of dispersion measures include: * Standard deviation * Interquartile ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Counting Process
A counting process is a stochastic process In probability theory and related fields, a stochastic () or random process is a mathematical object usually defined as a family of random variables in a probability space, where the index of the family often has the interpretation of time. Sto ... \ with values that are non-negative, integer, and non-decreasing: # N(t)\geq0. # N(t) is an integer. # If s\leq t then N(s)\leq N(t). If s [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fano Noise
Fano noise is a fluctuation of an electric charge obtained in a detector (in spite of constant value of the measured quantity, which is usually an energy), arising from processes in the detector. It was first described by Ugo Fano in 1947, as a fluctuation of amount of ion pairs produced by a charged particle of high energy in a gas. The amount of the ion pairs is proportional to the energy the particle loses in the gas, but with some error - due to the Fano noise. Surprisingly, the noise is usually smaller than a Poisson distribution noise (in which the variance is equal to the value - note the variance is average squared distance from the expected value), showing there is an interaction between ionization acts. A Fano factor was introduced to describe it, and the factor is almost independent of the energy measured (Fano computed it to change from 0.43 to 0.47 for ionization of atomic hydrogen by electrons of energy from 1keV to 100keV). Fano expected it to be between 1/3 and 1/2 f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ugo Fano
Ugo Fano (July 28, 1912 – February 13, 2001) was an Italian American physicist, notable for contributions to theoretical physics. Biography Ugo Fano was born into a wealthy Jewish family in Turin, Italy. His father was Gino Fano, a professor of mathematics. University studies Fano earned his doctorate in mathematics at the University of Turin in 1934, under Enrico Persico, with a thesis entitled ''Sul Calcolo dei Termini Spettrali e in Particolare dei Potenziali di Ionizzazione Nella Meccanica Quantistica'' (''On the Quantum Mechanical Calculation Spectral Terms and their Extension to Ionization''). As part of his PhD examination he also made two oral presentations entitled: ''Sulle Funzioni di Due o Più Variabili Complesse'' (''On the functions of two or more complex variables'') and ''Le Onde Elettromagnetiche di Maggi: Le Connessioni Asimmetriche Nella Geometria Non Riemanniana'' (''Maggi electromagnetic waves: asymmetric connections in non-Riemannian geometry''). E ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Standard Deviation
In statistics, the standard deviation is a measure of the amount of variation of the values of a variable about its Expected value, mean. A low standard Deviation (statistics), deviation indicates that the values tend to be close to the mean (also called the expected value) of the set, while a high standard deviation indicates that the values are spread out over a wider range. The standard deviation is commonly used in the determination of what constitutes an outlier and what does not. Standard deviation may be abbreviated SD or std dev, and is most commonly represented in mathematical texts and equations by the lowercase Greek alphabet, Greek letter Sigma, σ (sigma), for the population standard deviation, or the Latin script, Latin letter ''s'', for the sample standard deviation. The standard deviation of a random variable, Sample (statistics), sample, statistical population, data set, or probability distribution is the square root of its variance. (For a finite population, v ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Random Variable
A random variable (also called random quantity, aleatory variable, or stochastic variable) is a Mathematics, mathematical formalization of a quantity or object which depends on randomness, random events. The term 'random variable' in its mathematical definition refers to neither randomness nor variability but instead is a mathematical function (mathematics), function in which * the Domain of a function, domain is the set of possible Outcome (probability), outcomes in a sample space (e.g. the set \ which are the possible upper sides of a flipped coin heads H or tails T as the result from tossing a coin); and * the Range of a function, range is a measurable space (e.g. corresponding to the domain above, the range might be the set \ if say heads H mapped to -1 and T mapped to 1). Typically, the range of a random variable is a subset of the Real number, real numbers. Informally, randomness typically represents some fundamental element of chance, such as in the roll of a dice, d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Random Event
In common usage, randomness is the apparent or actual lack of definite pattern or predictability in information. A random sequence of events, symbols or steps often has no order and does not follow an intelligible pattern or combination. Individual random events are, by definition, unpredictable, but if there is a known probability distribution, the frequency of different outcomes over repeated events (or "trials") is predictable.Strictly speaking, the frequency of an outcome will converge almost surely to a predictable value as the number of trials becomes arbitrarily large. Non-convergence or convergence to a different value is possible, but has probability zero. Consistent non-convergence is thus evidence of the lack of a fixed probability distribution, as in many evolutionary processes. For example, when throwing two dice, the outcome of any particular roll is unpredictable, but a sum of 7 will tend to occur twice as often as 4. In this view, randomness is not haphazardne ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Poisson Point Process
In probability theory, statistics and related fields, a Poisson point process (also known as: Poisson random measure, Poisson random point field and Poisson point field) is a type of mathematical object that consists of points randomly located on a mathematical space with the essential feature that the points occur independently of one another. The process's name derives from the fact that the number of points in any given finite region follows a Poisson distribution. The process and the distribution are named after French mathematician Siméon Denis Poisson. The process itself was discovered independently and repeatedly in several settings, including experiments on radioactive decay, telephone call arrivals and actuarial science. This point process is used as a mathematical model for seemingly random processes in numerous disciplines including astronomy,G. J. Babu and E. D. Feigelson. Spatial point processes in astronomy. ''Journal of statistical planning and inference'', 50( ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
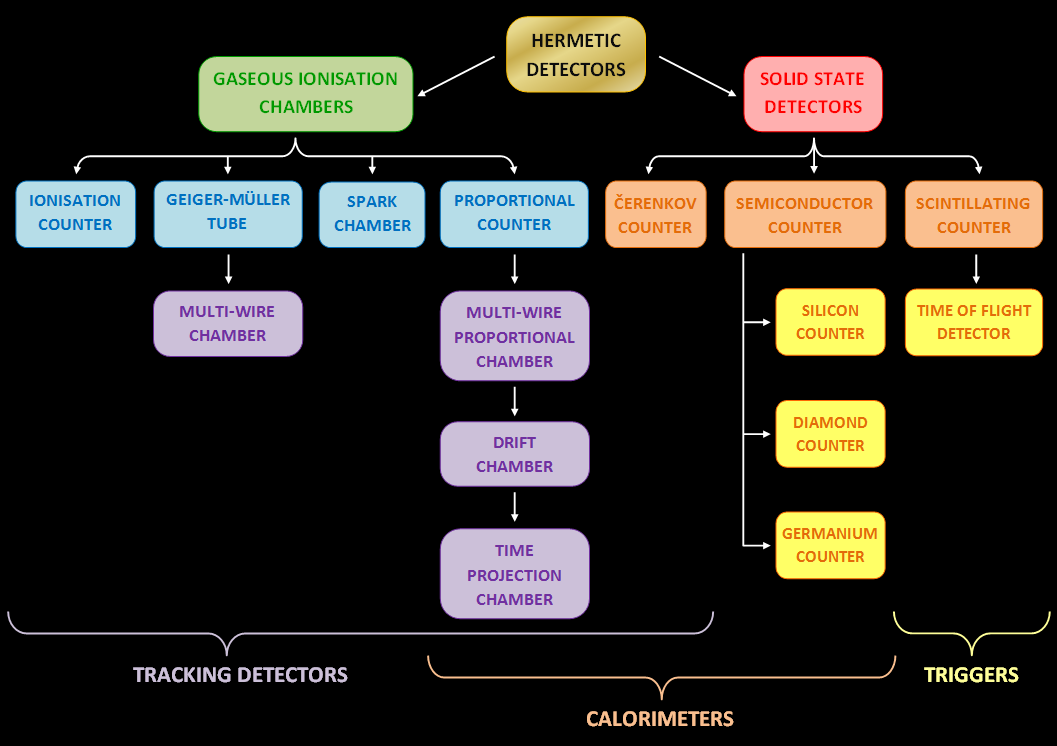
Particle Detector
In experimental and applied particle physics, nuclear physics, and nuclear engineering, a particle detector, also known as a radiation detector, is a device used to detect, track, and/or identify ionizing elementary particle, particles, such as those produced by nuclear decay, cosmic radiation, or reactions in a particle accelerator. Detectors can measure the particle energy and other attributes such as momentum, spin, charge, particle type, in addition to merely registering the presence of the particle. The operating of a nuclear radiation detector The operating principle of a nuclear radiation detector can be summarized as follows: The detector identifies high-energy particles or photons—such as alpha, beta, gamma radiation, or neutrons—through their interactions with the atoms of the detector material. These interactions generate a primary signal, which may involve ionization of gas, the creation of electron-hole pairs in semiconductors, or the emission of light in scint ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Full Width At Half Maximum
In a distribution, full width at half maximum (FWHM) is the difference between the two values of the independent variable at which the dependent variable is equal to half of its maximum value. In other words, it is the width of a spectrum curve measured between those points on the ''y''-axis which are half the maximum amplitude. Half width at half maximum (HWHM) is half of the FWHM if the function is symmetric. The term full duration at half maximum (FDHM) is preferred when the independent variable is time. FWHM is applied to such phenomena as the duration of pulse waveforms and the spectral width of sources used for optical communications and the resolution of spectrometers. The convention of "width" meaning "half maximum" is also widely used in signal processing to define bandwidth as "width of frequency range where less than half the signal's power is attenuated", i.e., the power is at least half the maximum. In signal processing terms, this is at most −3 dB of att ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |