|
Renewal Theory
Renewal theory is the branch of probability theory that generalizes the Poisson process for arbitrary holding times. Instead of exponentially distributed holding times, a renewal process may have any independent and identically distributed (IID) holding times that have finite expectation. A renewal-reward process additionally has a random sequence of rewards incurred at each holding time, which are IID but need not be independent of the holding times. A renewal process has asymptotic properties analogous to the strong law of large numbers and central limit theorem. The renewal function m(t) (expected number of arrivals) and reward function g(t) (expected reward value) are of key importance in renewal theory. The renewal function satisfies a recursive integral equation, the renewal equation. The key renewal equation gives the limiting value of the convolution of m'(t) with a suitable non-negative function. The superposition of renewal processes can be studied as a special case of M ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Theory
Probability theory or probability calculus is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expressing it through a set of axioms of probability, axioms. Typically these axioms formalise probability in terms of a probability space, which assigns a measure (mathematics), measure taking values between 0 and 1, termed the probability measure, to a set of outcomes called the sample space. Any specified subset of the sample space is called an event (probability theory), event. Central subjects in probability theory include discrete and continuous random variables, probability distributions, and stochastic processes (which provide mathematical abstractions of determinism, non-deterministic or uncertain processes or measured Quantity, quantities that may either be single occurrences or evolve over time in a random fashion). Although it is no ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coupling (probability)
In probability theory, coupling is a proof technique that allows one to compare two unrelated random variables (distributions) and by creating a random vector whose marginal distributions correspond to and respectively. The choice of is generally not unique, and the whole idea of "coupling" is about making such a choice so that and can be related in a particularly desirable way. Definition Using the standard formalism of probability theory, let X_1 and X_2 be two random variables defined on probability spaces (\Omega_1,F_1,P_1) and (\Omega_2,F_2,P_2). Then a coupling of X_1 and X_2 is a ''new'' probability space (\Omega,F,P) over which there are two random variables Y_1 and Y_2 such that Y_1 has the same distribution as X_1 while Y_2 has the same distribution as X_2. An interesting case is when Y_1 and Y_2 are ''not'' independent. Examples Random walk Assume two particles ''A'' and ''B'' perform a simple random walk in two dimensions, but they start from different poi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Residual Time
In the theory of renewal processes, a part of the mathematical theory of probability, the residual time or the forward recurrence time is the time between any given time t and the next epoch of the renewal process under consideration. In the context of random walks, it is also known as overshoot. Another way to phrase residual time is "how much more time is there to wait?". The residual time is very important in most of the practical applications of renewal processes: * In queueing theory, it determines the remaining time, that a newly arriving customer to a non-empty queue has to wait until being served. * In wireless networking, it determines, for example, the remaining lifetime of a wireless link on arrival of a new packet. * In dependability studies, it models the remaining lifetime of a component. * etc. Formal definition Consider a renewal process \, with ''holding times'' S_ and ''jump times'' (or renewal epochs) J_, and i\in\mathbb. The holding times S_ are non-negative, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Queueing Theory
Queueing theory is the mathematical study of waiting lines, or queues. A queueing model is constructed so that queue lengths and waiting time can be predicted. Queueing theory is generally considered a branch of operations research because the results are often used when making business decisions about the resources needed to provide a service. Queueing theory has its origins in research by Agner Krarup Erlang, who created models to describe the system of incoming calls at the Copenhagen Telephone Exchange Company. These ideas were seminal to the field of teletraffic engineering and have since seen applications in telecommunications, traffic engineering, computing, project management, and particularly industrial engineering, where they are applied in the design of factories, shops, offices, and hospitals. Spelling The spelling "queueing" over "queuing" is typically encountered in the academic research field. In fact, one of the flagship journals of the field is '' Queue ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
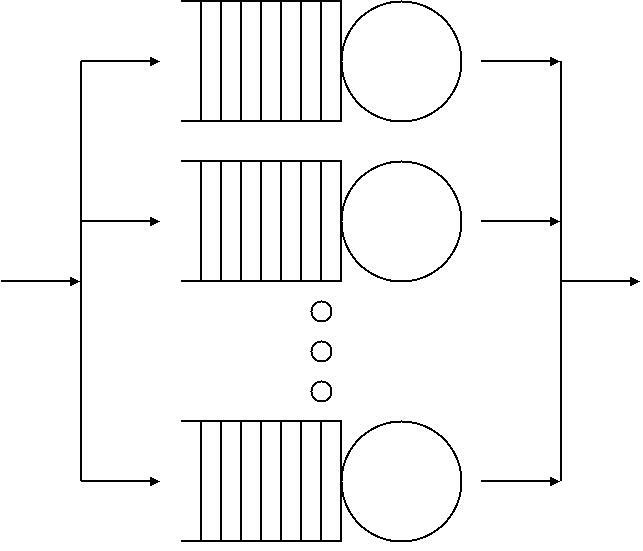
Palm–Khintchine Theorem
In probability theory, the Palm–Khintchine theorem, the work of Conny Palm and Aleksandr Khinchin, expresses that a large number of renewal processes, not necessarily Poissonian, when combined ("superimposed") will have Poissonian properties. It is used to generalise the behaviour of users or clients in queuing theory. It is also used in dependability and reliability modelling of computing and telecommunications. Theorem According to Heyman and Sobel (2003), the theorem states that the superposition of a large number of independent equilibrium renewal processes, each with a finite intensity, behaves asymptotically like a Poisson process: Let \, i=1,2,\ldots, m be independent renewal processes and \ be the superposition of these processes. Denote by X_ the time between the first and the second renewal epochs in process j. Define N_(t) the jth counting process, F_(t)=P(X_\leq t) and \lambda_=1/(E((X_)). If the following assumptions hold 1) For all sufficiently large m: ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuous-time Markov Process
A continuous-time Markov chain (CTMC) is a continuous stochastic process in which, for each state, the process will change state according to an exponential random variable and then move to a different state as specified by the probabilities of a stochastic matrix. An equivalent formulation describes the process as changing state according to the least value of a set of exponential random variables, one for each possible state it can move to, with the parameters determined by the current state. An example of a CTMC with three states \ is as follows: the process makes a transition after the amount of time specified by the holding time—an exponential random variable E_i, where ''i'' is its current state. Each random variable is independent and such that E_0\sim \text(6), E_1\sim \text(12) and E_2\sim \text(18). When a transition is to be made, the process moves according to the jump chain, a discrete-time Markov chain with stochastic matrix: :\begin 0 & \frac & \frac \\ \frac & 0 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compound Poisson Process
A compound Poisson process is a continuous-time stochastic process with jumps. The jumps arrive randomly according to a Poisson process and the size of the jumps is also random, with a specified probability distribution. To be precise, a compound Poisson process, parameterised by a rate \lambda > 0 and jump size distribution ''G'', is a process \ given by :Y(t) = \sum_^ D_i where, \ is the counting variable of a Poisson process with rate \lambda, and \ are independent and identically distributed random variables, with distribution function ''G'', which are also independent of \.\, When D_i are non-negative integer-valued random variables, then this compound Poisson process is known as a stuttering Poisson process. Properties of the compound Poisson process The expected value of a compound Poisson process can be calculated using a result known as Wald's equation as: :\operatorname E(Y(t)) = \operatorname E(D_1 + \cdots + D_) = \operatorname E(N(t))\operatorname E(D_1) = ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Campbell's Theorem (probability)
In probability theory and statistics, Campbell's theorem or the Campbell–Hardy theorem is either a particular equation or set of results relating to the Expected value, expectation of a Function (mathematics), function summed over a point process to an integral involving the Moment measure#First moment measure, mean measure of the point process, which allows for the calculation of expected value and variance of the random summation, sum. One version of the theorem,D. Stoyan, W. S. Kendall, J. Mecke. ''Stochastic geometry and its applications'', volume 2. Wiley Chichester, 1995. also known as Campbell's formula, entails an integral equation for the aforementioned sum over a general point process, and not necessarily a Poisson point process. There also exist equations involving moment measures and factorial moment measures that are considered versions of Campbell's formula. All these results are employed in probability and statistics with a particular importance in the theory of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cumulative Distribution Function
In probability theory and statistics, the cumulative distribution function (CDF) of a real-valued random variable X, or just distribution function of X, evaluated at x, is the probability that X will take a value less than or equal to x. Every probability distribution Support (measure theory), supported on the real numbers, discrete or "mixed" as well as Continuous variable, continuous, is uniquely identified by a right-continuous Monotonic function, monotone increasing function (a càdlàg function) F \colon \mathbb R \rightarrow [0,1] satisfying \lim_F(x)=0 and \lim_F(x)=1. In the case of a scalar continuous distribution, it gives the area under the probability density function from negative infinity to x. Cumulative distribution functions are also used to specify the distribution of multivariate random variables. Definition The cumulative distribution function of a real-valued random variable X is the function given by where the right-hand side represents the probability ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sampling Bias
In statistics, sampling bias is a bias (statistics), bias in which a sample is collected in such a way that some members of the intended statistical population, population have a lower or higher sampling probability than others. It results in a biased sample of a population (or non-human factors) in which all individuals, or instances, were not equally likely to have been selected. If this is not accounted for, results can be erroneously attributed to the phenomenon under study rather than to the method of sampling (statistics), sampling. Medical sources sometimes refer to sampling bias as ascertainment bias. Ascertainment bias has basically the same definition, but is still sometimes classified as a separate type of bias. Distinction from selection bias Sampling bias is usually classified as a subtype of selection bias, sometimes specifically termed sample selection bias, but some classify it as a separate type of bias. A distinction, albeit not universally accepted, of samplin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |