|
Faddeeva Function
The Faddeeva function or Kramp function is a scaled complex complementary error function, :w(z):=e^\operatorname(-iz) = \operatorname(-iz) =e^\left(1+\frac\int_0^z e^\textt\right). It is related to the Fresnel integral, to Dawson's integral, and to the Voigt function. The function arises in various physical problems, typically relating to electromagnetic responses in complicated media. * problems involving small-amplitude waves propagating through Maxwellian plasmas, and in particular appears in the plasma's permittivity from which dispersion relations are derived, hence it is sometimes referred to as the plasma dispersion function (although this name is sometimes used instead for the rescaled function defined by ''Fried and Conte'', 1961). * the infrared permittivity functions of amorphous oxides have resonances (due to phonons) that are sometimes too complicated to fit using simple harmonic oscillators. The Brendel–Bormann oscillator model uses an infinite superposition o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Faddeeva
In mathematics, the error function (also called the Gauss error function), often denoted by , is a function \mathrm: \mathbb \to \mathbb defined as: \operatorname z = \frac\int_0^z e^\,\mathrm dt. The integral here is a complex contour integral which is path-independent because \exp(-t^2) is holomorphic on the whole complex plane \mathbb. In many applications, the function argument is a real number, in which case the function value is also real. In some old texts, the error function is defined without the factor of \frac. This nonelementary integral is a sigmoid function that occurs often in probability, statistics, and partial differential equations. In statistics, for non-negative real values of , the error function has the following interpretation: for a real random variable that is normally distributed with mean 0 and standard deviation \frac, is the probability that falls in the range . Two closely related functions are the complementary error function \mathrm: \mathb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Partial Derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant (as opposed to the total derivative, in which all variables are allowed to vary). Partial derivatives are used in vector calculus and differential geometry. The partial derivative of a function f(x, y, \dots) with respect to the variable x is variously denoted by It can be thought of as the rate of change of the function in the x-direction. Sometimes, for the partial derivative of z with respect to x is denoted as \tfrac. Since a partial derivative generally has the same arguments as the original function, its functional dependence is sometimes explicitly signified by the notation, such as in: f'_x(x, y, \ldots), \frac (x, y, \ldots). The symbol used to denote partial derivatives is ∂. One of the first known uses of this symbol in mathematics is by Marquis de Condorcet from 1770, who used it for partial differ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
GNU Octave
GNU Octave is a scientific programming language for scientific computing and numerical computation. Octave helps in solving linear and nonlinear problems numerically, and for performing other numerical experiments using a language that is mostly compatible with MATLAB. It may also be used as a Batch processing, batch-oriented language. As part of the GNU Project, it is free software under the terms of the GNU General Public License. History The project was conceived around 1988. At first it was intended to be a companion to a chemical reactor design course. Full development was started by John W. Eaton in 1992. The first alpha release dates back to 4 January 1993 and on 17 February 1994 version 1.0 was released. Version 9.2.0 was released on 7 June 2024. The program is named after Octave Levenspiel, a former professor of the principal author. Levenspiel was known for his ability to perform quick back-of-the-envelope calculations. Development history Developments In addition ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Plug-in (computing)
In computing, a plug-in (also spelled plugin) or add-in (also addin, add-on, or addon) is a software component that extends the functionality of an existing software system without requiring the system to be software build, re-built. A plug-in software feature, feature is one way that a system can be customizable. Applications support plug-ins for a variety of reasons including: * Enable third-party developers to extend an application * Support easily adding new features * Reduce the size of an application by not loading unused features * Separate source code from an application because of incompatible software licenses Examples Examples of plug-in use for various categories of applications: * Digital audio workstations and audio editing software use audio plug-ins to generate, process or analyze sound. Ardour (software), Ardour, Audacity (audio editor), Audacity, Cubase, FL Studio, Logic Pro, Logic Pro X and Pro Tools are examples of such systems. * Email clients use plug-i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
MIT License
The MIT License is a permissive software license originating at the Massachusetts Institute of Technology (MIT) in the late 1980s. As a permissive license, it puts very few restrictions on reuse and therefore has high license compatibility. Unlike copyleft software licenses, the MIT License also permits reuse within proprietary software, provided that all copies of the software or its substantial portions include a copy of the terms of the MIT License and also a copyright notice. In 2015, the MIT License was the most popular software license on GitHub, and was still the most popular in 2025. Notable projects that use the MIT License include the X Window System, Ruby on Rails, Node.js, Lua (programming language), Lua, jQuery, .NET, Angular (web framework), Angular, and React (JavaScript library), React. License terms The MIT License has the identifier MIT in the SPDX License List. It is also known as the "#Ambiguity and variants, Expat License". It has the following terms: Co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Free And Open Source
Free and open-source software (FOSS) is software available under a license that grants users the right to use, modify, and distribute the software modified or not to everyone free of charge. FOSS is an inclusive umbrella term encompassing free software and open-source software. The rights guaranteed by FOSS originate from the "Four Essential Freedoms" of '' The Free Software Definition'' and the criteria of '' The Open Source Definition''. All FOSS can have publicly available source code, but not all source-available software is FOSS. FOSS is the opposite of proprietary software, which is licensed restrictively or has undisclosed source code. The historical precursor to FOSS was the hobbyist and academic public domain software ecosystem of the 1960s to 1980s. Free and open-source operating systems such as Linux distributions and descendants of BSD are widely used, powering millions of servers, desktops, smartphones, and other devices. Free-software licenses and open-source ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
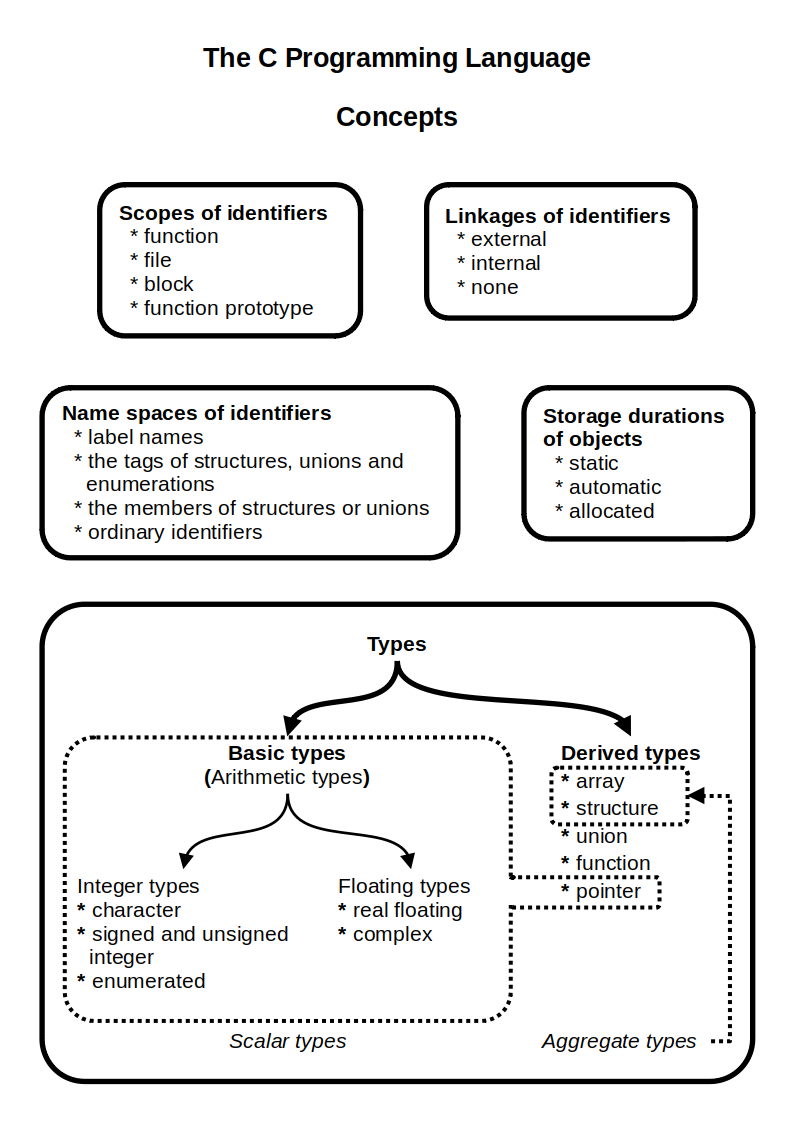
C (programming Language)
C (''pronounced'' '' – like the letter c'') is a general-purpose programming language. It was created in the 1970s by Dennis Ritchie and remains very widely used and influential. By design, C's features cleanly reflect the capabilities of the targeted Central processing unit, CPUs. It has found lasting use in operating systems code (especially in Kernel (operating system), kernels), device drivers, and protocol stacks, but its use in application software has been decreasing. C is commonly used on computer architectures that range from the largest supercomputers to the smallest microcontrollers and embedded systems. A successor to the programming language B (programming language), B, C was originally developed at Bell Labs by Ritchie between 1972 and 1973 to construct utilities running on Unix. It was applied to re-implementing the kernel of the Unix operating system. During the 1980s, C gradually gained popularity. It has become one of the most widely used programming langu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Free And Open-source Software
Free and open-source software (FOSS) is software available under a license that grants users the right to use, modify, and distribute the software modified or not to everyone free of charge. FOSS is an inclusive umbrella term encompassing free software and open-source software. The rights guaranteed by FOSS originate from the "Four Essential Freedoms" of '' The Free Software Definition'' and the criteria of '' The Open Source Definition''. All FOSS can have publicly available source code, but not all source-available software is FOSS. FOSS is the opposite of proprietary software, which is licensed restrictively or has undisclosed source code. The historical precursor to FOSS was the hobbyist and academic public domain software ecosystem of the 1960s to 1980s. Free and open-source operating systems such as Linux distributions and descendants of BSD are widely used, powering millions of servers, desktops, smartphones, and other devices. Free-software licenses and open-so ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
MATLAB
MATLAB (an abbreviation of "MATrix LABoratory") is a proprietary multi-paradigm programming language and numeric computing environment developed by MathWorks. MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages. Although MATLAB is intended primarily for numeric computing, an optional toolbox uses the MuPAD symbolic engine allowing access to symbolic computing abilities. An additional package, Simulink, adds graphical multi-domain simulation and model-based design for dynamic and embedded systems. , MATLAB has more than four million users worldwide. They come from various backgrounds of engineering, science, and economics. , more than 5000 global colleges and universities use MATLAB to support instruction and research. History Origins MATLAB was invented by mathematician and computer programmer Cleve Moler. The idea for MATLAB was base ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
ACM Transactions On Mathematical Software
''ACM Transactions on Mathematical Software'' (''TOMS'') is a quarterly scientific journal that aims to disseminate the latest findings of note in the field of numeric, symbolic, algebraic, and geometric computing applications. The journal publishes two kinds of articles: Regular research papers that advance the development of algorithms and software for mathematical computing, and "algorithms papers" that describe a specific implementation of an algorithm and that are accompanied by the source code for this algorithm. Algorithms described in the transactions are generally published in the ''Collected Algorithms of the ACM (CALGO)''. Algorithms published since 1975 (and some earlier ones) are all still available. Software that accompanies algorithm papers is accessible by anyone via the CALGO website. History ACM Transactions on Mathematical Software is one of the oldest scientific journals specifically dedicated to mathematical algorithms and their implementation in software, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Walter Gautschi
Walter Gautschi (; ; born December 11, 1927) is a Swiss-born American mathematician, writer and professor emeritus of Computer science and Mathematics at Purdue University in West Lafayette, Indiana. He is primarily known for his contributions to numerical analysis and has authored over 200 papers in his area and published four books. Early life and education Gautschi was born December 11, 1927, in Basel, Switzerland, to Heinrich Gautschi (1901-1975). His paternal family originally hailed from Reinach. His patrilineal uncle, Adolf Eduard Gautschi, was a custodian and landscape painter. He had one twin brother Werner (1927-1959). He completed a Ph.D. in mathematics from the University of Basel on the thesis ''Analyse graphischer Integrationsmethoden'' advised by Alexander Ostrowski and Andreas Speiser (1953). Career Since then, he did postdoctoral work as a Janggen-Pöhn Research, Fellow at the ''Istituto Nazionale per le Applicazioni del Calcolo'' in Rome (1954) and at the H ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |