|
Factor Analysis Of Mixed Data
In statistics, factor analysis of mixed data or factorial analysis of mixed data (FAMD, in the French original: ''AFDM'' or ''Analyse Factorielle de Données Mixtes''), is the factorial method devoted to data tables in which a group of individuals is described both by quantitative and qualitative variables. It belongs to the exploratory methods developed by the French school called ''Analyse des données'' (data analysis) founded by Jean-Paul Benzécri. The term ''mixed'' refers to the use of both quantitative and qualitative variables. Roughly, we can say that FAMD works as a principal components analysis (PCA) for quantitative variables and as a multiple correspondence analysis (MCA) for qualitative variables. Scope When data include both types of variables but the active variables being homogeneous, PCA or MCA can be used. Indeed, it is easy to include supplementary quantitative variables in MCA by the correlation coefficients between the variables and factors on individu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German: '' Statistik'', "description of a state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of surveys and experiments.Dodge, Y. (2006) ''The Oxford Dictionary of Statistical Terms'', Oxford University Press. When census data cannot be collected, statisticians collect data by developing specific experiment designs and survey samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample to the population as a whole. An ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Factor Analysis
Factor analysis is a statistical method used to describe variability among observed, correlated variables in terms of a potentially lower number of unobserved variables called factors. For example, it is possible that variations in six observed variables mainly reflect the variations in two unobserved (underlying) variables. Factor analysis searches for such joint variations in response to unobserved latent variables. The observed variables are modelled as linear combinations of the potential factors plus " error" terms, hence factor analysis can be thought of as a special case of errors-in-variables models. Simply put, the factor loading of a variable quantifies the extent to which the variable is related to a given factor. A common rationale behind factor analytic methods is that the information gained about the interdependencies between observed variables can be used later to reduce the set of variables in a dataset. Factor analysis is commonly used in psychometrics, per ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jean-Paul Benzécri
Jean-Paul Benzécri was a French mathematician and statistician. He studied at École Normale Supérieure and was professor at Université de Rennes and later for most of his career at the Paris Institute of Statistics (l'Institut de Statistique de l'Université de Paris), Université Pierre-et-Marie-Curie in Paris. He is most known for his specific inductive approach to data analysis which led to the creation of Correspondence analysis, a statistical technique for analyzing contingency tables and for the invention of the nearest-neighbor chain algorithm for agglomerative hierarchical clustering. Early life Jean-Paul Benzécri was born in Oran, Algeria, in 1932, where his father was a doctor. He attended high school in Lycée Lamoricière, Oran and Lycée Bugeaud, Alger. In 1950, he was first in the entrance examination to the ENS (École Normale Supérieure) in Paris and again in 1953 to the "Agrégation de Mathématiques", a national teacher's diploma examination. He then did s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Principal Components Analysis
Principal component analysis (PCA) is a popular technique for analyzing large datasets containing a high number of dimensions/features per observation, increasing the interpretability of data while preserving the maximum amount of information, and enabling the visualization of multidimensional data. Formally, PCA is a statistical technique for reducing the dimensionality of a dataset. This is accomplished by linearly transforming the data into a new coordinate system where (most of) the variation in the data can be described with fewer dimensions than the initial data. Many studies use the first two principal components in order to plot the data in two dimensions and to visually identify clusters of closely related data points. Principal component analysis has applications in many fields such as population genetics, microbiome studies, and atmospheric science. The principal components of a collection of points in a real coordinate space are a sequence of p unit vectors, where t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multiple Correspondence Analysis
In statistics, multiple correspondence analysis (MCA) is a data analysis technique for nominal categorical data, used to detect and represent underlying structures in a data set. It does this by representing data as points in a low-dimensional Euclidean space. The procedure thus appears to be the counterpart of principal component analysis for categorical data. MCA can be viewed as an extension of simple correspondence analysis (CA) in that it is applicable to a large set of categorical variables. As an extension of correspondence analysis MCA is performed by applying the CA algorithm to either an indicator matrix (also called ''complete disjunctive table'' – CDT) or a ''Burt table'' formed from these variables. An indicator matrix is an individuals × variables matrix, where the rows represent individuals and the columns are dummy variables representing categories of the variables. Analyzing the indicator matrix allows the direct representation of individuals as points in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Correlation Coefficient
A correlation coefficient is a numerical measure of some type of correlation, meaning a statistical relationship between two variables. The variables may be two columns of a given data set of observations, often called a sample, or two components of a multivariate random variable with a known distribution. Several types of correlation coefficient exist, each with their own definition and own range of usability and characteristics. They all assume values in the range from −1 to +1, where ±1 indicates the strongest possible agreement and 0 the strongest possible disagreement. As tools of analysis, correlation coefficients present certain problems, including the propensity of some types to be distorted by outliers and the possibility of incorrectly being used to infer a causal relationship between the variables (for more, see Correlation does not imply causation). Types There are several different measures for the degree of correlation in data, depending on the kind of data ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Correlation Ratio
In statistics, the correlation ratio is a measure of the curvilinear relationship between the statistical dispersion within individual categories and the dispersion across the whole population or sample. The measure is defined as the ''ratio'' of two standard deviations representing these types of variation. The context here is the same as that of the intraclass correlation coefficient, whose value is the square of the correlation ratio. Definition Suppose each observation is ''yxi'' where ''x'' indicates the category that observation is in and ''i'' is the label of the particular observation. Let ''nx'' be the number of observations in category ''x'' and :\overline_x=\frac and \overline=\frac, where \overline_x is the mean of the category ''x'' and \overline is the mean of the whole population. The correlation ratio η (eta) is defined as to satisfy :\eta^2 = \frac which can be written as :\eta^2 = \frac, \text^2 = \frac \text ^2 = \frac, i.e. the weighted variance of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
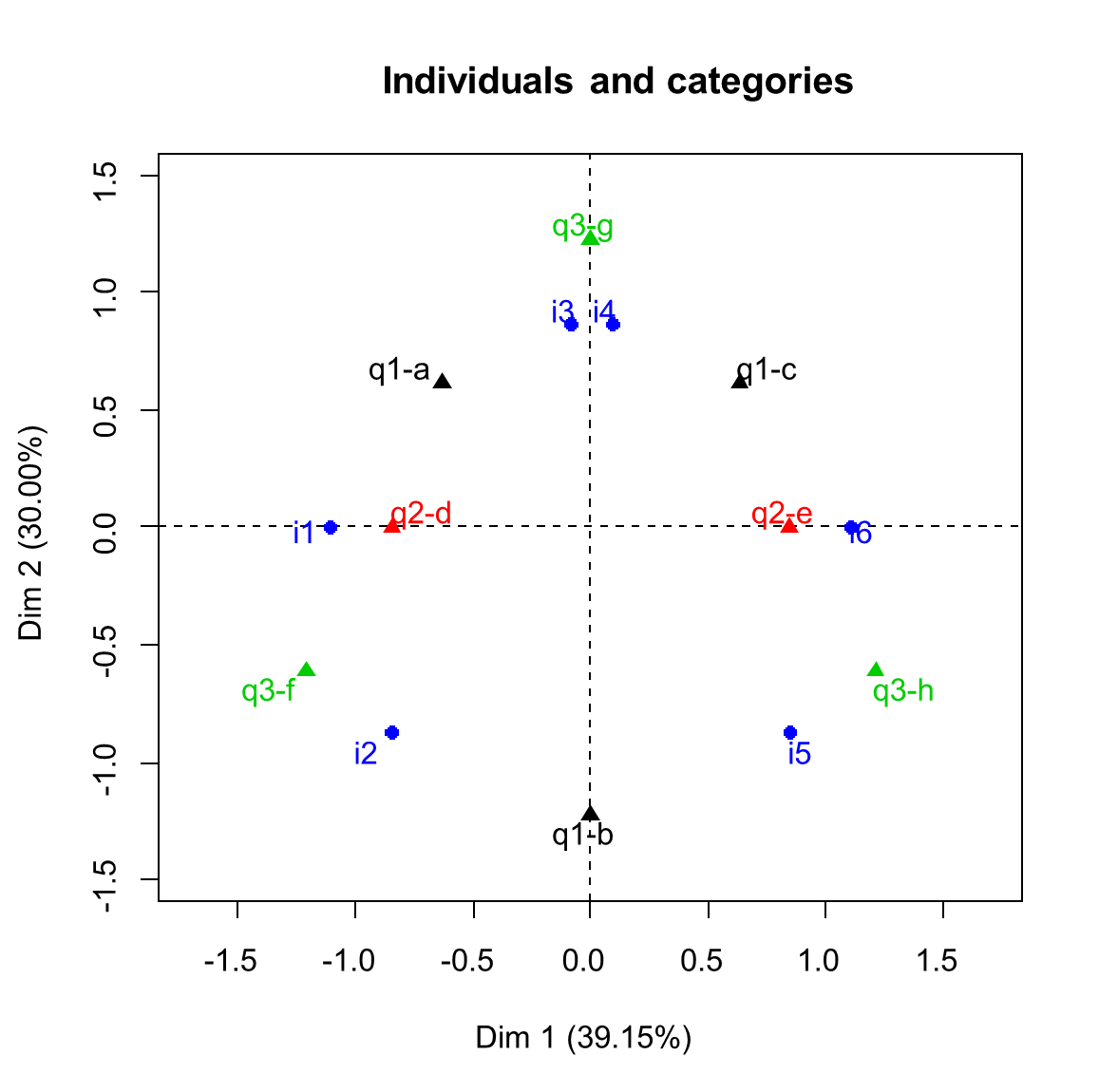
Relationship Square
In statistics, the relationship square is a graphical representation for use in the factorial analysis of a table ''individuals'' x ''variables''. This representation completes classical representations provided by principal component analysis (PCA) or multiple correspondence analysis (MCA), namely those of individuals, of quantitative variables (correlation circle) and of the categories of qualitative variables (at the centroid of the individuals who possess them). It is especially important in factor analysis of mixed data (FAMD) and in multiple factor analysis (MFA). Definition of ''relationship square'' in the MCA frame The first interest of the relationship square is to represent the variables themselves, not their categories, which is all the more valuable as there are many variables. For this, we calculate for each qualitative variable j and each factor F_s ( F_s , rank s factor, is the vector of coordinates of the individuals along the axis of rank s ; in PCA, F_s i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fig2FADM
The fig is the edible fruit of ''Ficus carica'', a species of small tree in the flowering plant family Moraceae. Native to the Mediterranean and western Asia, it has been cultivated since ancient times and is now widely grown throughout the world, both for its fruit and as an ornamental plant.''The Fig: its History, Culture, and Curing'', Gustavus A. Eisen, Washington, Govt. print. off., 1901 ''Ficus carica'' is the type species of the genus ''Ficus'', containing over 800 tropical and subtropical plant species. A fig plant is a small deciduous tree or large shrub growing up to tall, with smooth white bark. Its large leaves have three to five deep lobes. Its fruit (referred to as syconium, a type of multiple fruit) is tear-shaped, long, with a green skin that may ripen toward purple or brown, and sweet soft reddish flesh containing numerous crunchy seeds. The milky sap of the green parts is an irritant to human skin. In the Northern Hemisphere, fresh figs are in season from lat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |