|
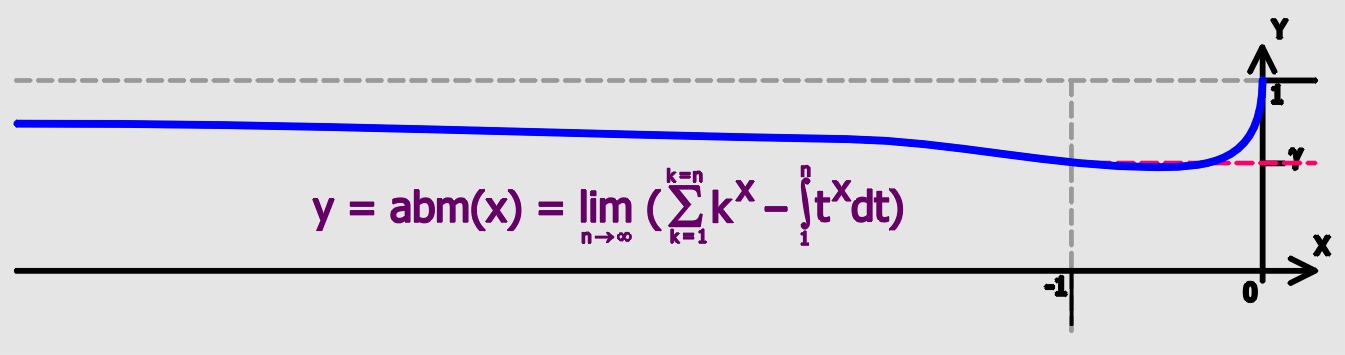
Euler–Mascheroni Constant
Euler's constant (sometimes also called the Euler–Mascheroni constant) is a mathematical constant usually denoted by the lowercase Greek letter gamma (). It is defined as the limiting difference between the harmonic series and the natural logarithm, denoted here by \log: :\begin \gamma &= \lim_\left(-\log n + \sum_^n \frac1\right)\\ px&=\int_1^\infty\left(-\frac1x+\frac1\right)\,dx. \end Here, \lfloor x\rfloor represents the floor function. The numerical value of Euler's constant, to 50 decimal places, is: : History The constant first appeared in a 1734 paper by the Swiss mathematician Leonhard Euler, titled ''De Progressionibus harmonicis observationes'' (Eneström Index 43). Euler used the notations and for the constant. In 1790, Italian mathematician Lorenzo Mascheroni used the notations and for the constant. The notation appears nowhere in the writings of either Euler or Mascheroni, and was chosen at a later time perhaps because of the constant's connection ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euler's Number
The number , also known as Euler's number, is a mathematical constant approximately equal to 2.71828 that can be characterized in many ways. It is the base of a logarithm, base of the natural logarithms. It is the Limit of a sequence, limit of as approaches infinity, an expression that arises in the study of compound interest. It can also be calculated as the sum of the infinite Series (mathematics), series e = \sum\limits_^ \frac = 1 + \frac + \frac + \frac + \cdots. It is also the unique positive number such that the graph of the function has a slope of 1 at . The (natural) exponential function is the unique function that equals its own derivative and satisfies the equation ; hence one can also define as . The natural logarithm, or logarithm to base , is the inverse function to the natural exponential function. The natural logarithm of a number can be defined directly as the integral, area under the curve between and , in which case is the value of for which ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Laurent Series
In mathematics, the Laurent series of a complex function f(z) is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where a Taylor series expansion cannot be applied. The Laurent series was named after and first published by Pierre Alphonse Laurent in 1843. Karl Weierstrass may have discovered it first in a paper written in 1841, but it was not published until after his death.. Definition The Laurent series for a complex function f(z) about a point c is given by f(z) = \sum_^\infty a_n(z-c)^n, where a_n and c are constants, with a_n defined by a line integral that generalizes Cauchy's integral formula: a_n =\frac\oint_\gamma \frac \, dz. The path of integration \gamma is counterclockwise around a Jordan curve enclosing c and lying in an annulus A in which f(z) is holomorphic (analytic). The expansion for f(z) will then be valid anywhere inside the annulus. The annulus is shown in red ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mean
There are several kinds of mean in mathematics, especially in statistics. Each mean serves to summarize a given group of data, often to better understand the overall value (magnitude and sign) of a given data set. For a data set, the ''arithmetic mean'', also known as "arithmetic average", is a measure of central tendency of a finite set of numbers: specifically, the sum of the values divided by the number of values. The arithmetic mean of a set of numbers ''x''1, ''x''2, ..., x''n'' is typically denoted using an overhead bar, \bar. If the data set were based on a series of observations obtained by sampling from a statistical population, the arithmetic mean is the ''sample mean'' (\bar) to distinguish it from the mean, or expected value, of the underlying distribution, the ''population mean'' (denoted \mu or \mu_x).Underhill, L.G.; Bradfield d. (1998) ''Introstat'', Juta and Company Ltd.p. 181/ref> Outside probability and statistics, a wide range of other notions of mean are o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Renormalization
Renormalization is a collection of techniques in quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, that are used to treat infinities arising in calculated quantities by altering values of these quantities to compensate for effects of their self-interactions. But even if no infinities arose in loop diagrams in quantum field theory, it could be shown that it would be necessary to renormalize the mass and fields appearing in the original Lagrangian. For example, an electron theory may begin by postulating an electron with an initial mass and charge. In quantum field theory a cloud of virtual particles, such as photons, positrons, and others surrounds and interacts with the initial electron. Accounting for the interactions of the surrounding particles (e.g. collisions at different energies) shows that the electron-system behaves as if it had a different mass and charge than initially postulated. Renormalization, in th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bessel's Equation
Bessel functions, first defined by the mathematician Daniel Bernoulli and then generalized by Friedrich Bessel, are canonical solutions of Bessel's differential equation x^2 \frac + x \frac + \left(x^2 - \alpha^2 \right)y = 0 for an arbitrary complex number \alpha, the ''order'' of the Bessel function. Although \alpha and -\alpha produce the same differential equation, it is conventional to define different Bessel functions for these two values in such a way that the Bessel functions are mostly smooth functions of \alpha. The most important cases are when \alpha is an integer or half-integer. Bessel functions for integer \alpha are also known as cylinder functions or the cylindrical harmonics because they appear in the solution to Laplace's equation in cylindrical coordinates. Spherical Bessel functions with half-integer \alpha are obtained when the Helmholtz equation is solved in spherical coordinates. Applications of Bessel functions The Bessel function is a generalization ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mertens' Theorems
In number theory, Mertens' theorems are three 1874 results related to the density of prime numbers proved by Franz Mertens.F. Mertens. J. reine angew. Math. 78 (1874), 46–6Ein Beitrag zur analytischen Zahlentheorie/ref> "Mertens' theorem" may also refer to his theorem in analysis. Theorems In the following, let p\le n mean all primes not exceeding ''n''. Mertens' first theorem: : \sum_ \frac - \log n does not exceed 2 in absolute value for any n\ge 2. () Mertens' second theorem: :\lim_\left(\sum_\frac1p -\log\log n-M\right) =0, where ''M'' is the Meissel–Mertens constant (). More precisely, Mertens proves that the expression under the limit does not in absolute value exceed : \frac 4 +\frac 2 for any n\ge 2. Mertens' third theorem: :\lim_\log n\prod_\left(1-\frac1p\right)=e^ \approx 0.561459483566885, where γ is the Euler–Mascheroni constant (). Changes in sign In a paper on the growth rate of the sum-of-divisors function published in 1983, Guy Robin pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Meissel–Mertens Constant
The Meissel–Mertens constant (named after Ernst Meissel and Franz Mertens), also referred to as Mertens constant, Kronecker's constant, Hadamard– de la Vallée-Poussin constant or the prime reciprocal constant, is a mathematical constant in number theory, defined as the limiting difference between the harmonic series summed only over the primes and the natural logarithm of the natural logarithm: :M = \lim_ \left( \sum_ \frac - \ln(\ln n) \right)=\gamma + \sum_ \left \ln\! \left( 1 - \frac \right) + \frac \right Here γ is the Euler–Mascheroni constant, which has an analogous definition involving a sum over all integers (not just the primes). The value of ''M'' is approximately :''M'' ≈ 0.2614972128476427837554268386086958590516... . Mertens' second theorem establishes that the limit exists. The fact that there are two logarithms (log of a log) in the limit for the Meissel–Mertens constant may be thought of as a consequence of the combination of the prime number t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Field Theory
In theoretical physics, quantum field theory (QFT) is a theoretical framework that combines classical field theory, special relativity, and quantum mechanics. QFT is used in particle physics to construct physical models of subatomic particles and in condensed matter physics to construct models of quasiparticles. QFT treats particles as excited states (also called Quantum, quanta) of their underlying quantum field (physics), fields, which are more fundamental than the particles. The equation of motion of the particle is determined by minimization of the Lagrangian, a functional of fields associated with the particle. Interactions between particles are described by interaction terms in the Lagrangian (field theory), Lagrangian involving their corresponding quantum fields. Each interaction can be visually represented by Feynman diagrams according to perturbation theory (quantum mechanics), perturbation theory in quantum mechanics. History Quantum field theory emerged from the wo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Feynman Diagram
In theoretical physics, a Feynman diagram is a pictorial representation of the mathematical expressions describing the behavior and interaction of subatomic particles. The scheme is named after American physicist Richard Feynman, who introduced the diagrams in 1948. The interaction of subatomic particles can be complex and difficult to understand; Feynman diagrams give a simple visualization of what would otherwise be an arcane and abstract formula. According to David Kaiser, "Since the middle of the 20th century, theoretical physicists have increasingly turned to this tool to help them undertake critical calculations. Feynman diagrams have revolutionized nearly every aspect of theoretical physics." While the diagrams are applied primarily to quantum field theory, they can also be used in other fields, such as solid-state theory. Frank Wilczek wrote that the calculations that won him the 2004 Nobel Prize in Physics "would have been literally unthinkable without Feynman diagra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dimensional Regularization
__NOTOC__ In theoretical physics, dimensional regularization is a method introduced by Giambiagi and Bollini as well as – independently and more comprehensively – by 't Hooft and Veltman for regularizing integrals in the evaluation of Feynman diagrams; in other words, assigning values to them that are meromorphic functions of a complex parameter ''d'', the analytic continuation of the number of spacetime dimensions. Dimensional regularization writes a Feynman integral as an integral depending on the spacetime dimension ''d'' and the squared distances (''x''''i''−''x''''j'')2 of the spacetime points ''x''''i'', ... appearing in it. In Euclidean space, the integral often converges for −Re(''d'') sufficiently large, and can be analytically continued from this region to a meromorphic function defined for all complex ''d''. In general, there will be a pole at the physical value (usually 4) of ''d'', which needs to be canceled by renormalization to obtain physical ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Divisor Function
In mathematics, and specifically in number theory, a divisor function is an arithmetic function related to the divisors of an integer. When referred to as ''the'' divisor function, it counts the ''number of divisors of an integer'' (including 1 and the number itself). It appears in a number of remarkable identities, including relationships on the Riemann zeta function and the Eisenstein series of modular forms. Divisor functions were studied by Ramanujan, who gave a number of important Modular arithmetic, congruences and identity (mathematics), identities; these are treated separately in the article Ramanujan's sum. A related function is the divisor summatory function, which, as the name implies, is a sum over the divisor function. Definition The sum of positive divisors function σ''z''(''n''), for a real or complex number ''z'', is defined as the summation, sum of the ''z''th Exponentiation, powers of the positive divisors of ''n''. It can be expressed in Summation#Capital ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euler's Totient Function
In number theory, Euler's totient function counts the positive integers up to a given integer that are relatively prime to . It is written using the Greek letter phi as \varphi(n) or \phi(n), and may also be called Euler's phi function. In other words, it is the number of integers in the range for which the greatest common divisor is equal to 1. The integers of this form are sometimes referred to as totatives of . For example, the totatives of are the six numbers 1, 2, 4, 5, 7 and 8. They are all relatively prime to 9, but the other three numbers in this range, 3, 6, and 9 are not, since and . Therefore, . As another example, since for the only integer in the range from 1 to is 1 itself, and . Euler's totient function is a multiplicative function, meaning that if two numbers and are relatively prime, then . This function gives the order of the multiplicative group of integers modulo (the group of units of the ring \Z/n\Z). It is also used for defining the RSA e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |