|
Ehrenfest Equations
Ehrenfest equations (named after Paul Ehrenfest) are equations which describe changes in specific heat capacity and derivatives of specific volume in second-order phase transitions. The Clausius–Clapeyron relation does not make sense for second-order phase transitions,Sivuhin D.V. General physics course. V.2. ''Thermodynamics and molecular physics''. 2005 as both specific entropy and specific volume do not change in second-order phase transitions. Quantitative consideration Ehrenfest equations are the consequence of continuity of specific entropy s and specific volume v, which are first derivatives of specific Gibbs free energy – in second-order phase transitions. If one considers specific entropy s as a function of temperature and pressure, then its differential is: ds = \left( \right)_P dT + \left( \right)_T dP. As \left( \right)_P = , \left( \right)_T = - \left( \right)_P , then the differential of specific entropy also is: d = dT - \left( \right)_P dP, where i= ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Paul Ehrenfest
Paul Ehrenfest (18 January 1880 – 25 September 1933) was an Austrian theoretical physicist, who made major contributions to the field of statistical mechanics and its relations with quantum mechanics, including the theory of phase transition and the Ehrenfest theorem. He bonded with Albert Einstein on a visit to Prague in 1912 and became a professor in Leiden, where he frequently hosted Einstein. Biography Paul Ehrenfest was born and grew up in Vienna to Jewish parents from Loštice in Moravia (now part of the Czech Republic). His parents, Sigmund Ehrenfest and Johanna Jellinek, ran a grocery store. Although the family was not overly religious, Paul studied Hebrew and the history of the Jewish people. Later, he always emphasized his Jewish roots. Ehrenfest excelled in grade school but did not do well at the Akademisches Gymnasium, his best subject being mathematics. After transferring to the Franz Josef Gymnasium, his marks improved. In 1899, he passed the final exams. He m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
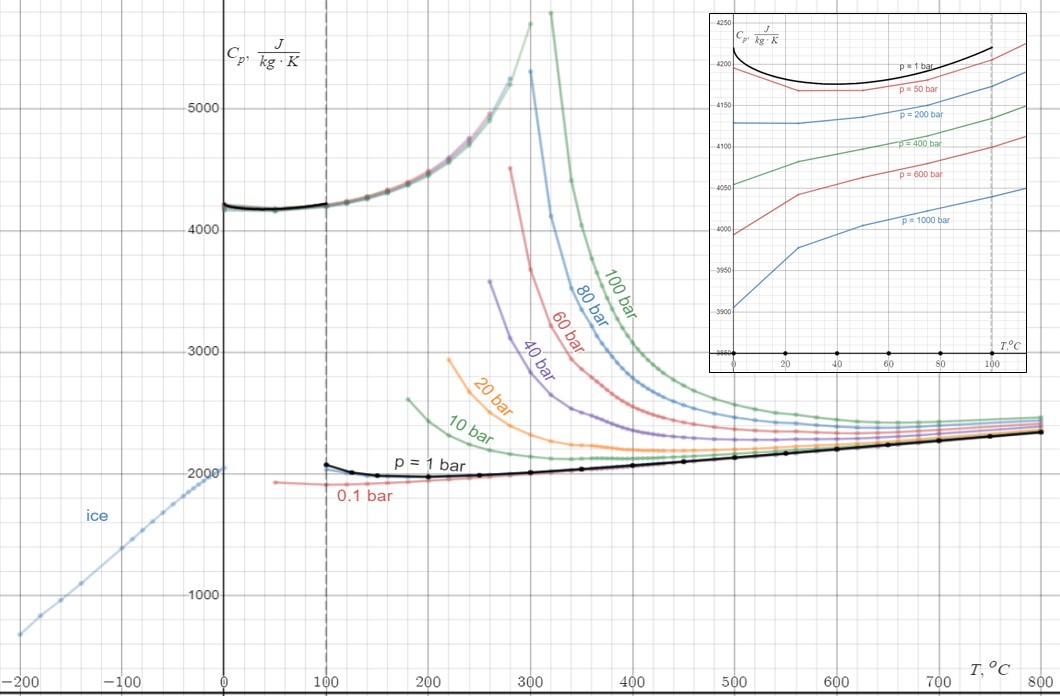
Heat Capacity
Heat capacity or thermal capacity is a physical property of matter, defined as the amount of heat to be supplied to an object to produce a unit change in its temperature. The SI unit of heat capacity is joule per kelvin (J/K). Heat capacity is an extensive property. The corresponding intensive property is the specific heat capacity, found by dividing the heat capacity of an object by its mass. Dividing the heat capacity by the amount of substance in moles yields its molar heat capacity. The volumetric heat capacity measures the heat capacity per volume. In architecture and civil engineering, the heat capacity of a building is often referred to as its thermal mass. Definition Basic definition The heat capacity of an object, denoted by C, is the limit : C = \lim_\frac, where \Delta Q is the amount of heat that must be added to the object (of mass ''M'') in order to raise its temperature by \Delta T. The value of this parameter usually varies considerably depending on the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Specific Volume
In thermodynamics, the specific volume of a substance (symbol: , nu) is an intrinsic property of the substance, defined as the ratio of the substance's volume () to its mass (). It is the reciprocal of density (rho) and it is related to the molar volume and molar mass: :\nu = \frac = \rho^ = \frac The standard unit of specific volume is cubic meters per kilogram (m3/kg), but other units include ft3/lb, ft3/slug, or mL/g. Specific volume for an ideal gas is related to the molar gas constant () and the gas's temperature (), pressure (), and molar mass () as shown: Since PV = and n = \frac : \nu = \frac = \frac Applications Specific volume is commonly applied to: * Molar volume * Volume (thermodynamics) * Partial molar volume Imagine a variable-volume, airtight chamber containing a certain number of atoms of oxygen gas. Consider the following four examples: * If the chamber is made smaller without allowing gas in or out, the density increases and the specific volume decreases ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phase Transitions
In chemistry, thermodynamics, and other related fields, a phase transition (or phase change) is the physical process of transition between one state of a medium and another. Commonly the term is used to refer to changes among the basic states of matter: solid, liquid, and gas, and in rare cases, plasma. A phase of a thermodynamic system and the states of matter have uniform physical properties. During a phase transition of a given medium, certain properties of the medium change as a result of the change of external conditions, such as temperature or pressure. This can be a discontinuous change; for example, a liquid may become gas upon heating to its boiling point, resulting in an abrupt change in volume. The identification of the external conditions at which a transformation occurs defines the phase transition point. Types of phase transition At the phase transition point for a substance, for instance the boiling point, the two phases involved - liquid and vapor, have identic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Clausius–Clapeyron Relation
The Clausius–Clapeyron relation, named after Rudolf Clausius and Benoît Paul Émile Clapeyron, specifies the temperature dependence of pressure, most importantly vapor pressure, at a discontinuous phase transition between two phases of matter of a single constituent. Its relevance to meteorology and climatology is the increase of the water-holding capacity of the atmosphere by about 7% for every 1 °C (1.8 °F) rise in temperature. Definition On a pressure–temperature (''P''–''T'') diagram, the line separating the two phases is known as the coexistence curve. The Clapeyron relation gives the slope of the tangents to this curve. Mathematically, :\frac = \frac=\frac, where \mathrmP/\mathrmT is the slope of the tangent to the coexistence curve at any point, L is the specific latent heat, T is the temperature, \Delta v is the specific volume change of the phase transition, and \Delta s is the specific entropy change of the phase transition. The Clausius–Clape ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Entropy
Entropy is a scientific concept, as well as a measurable physical property, that is most commonly associated with a state of disorder, randomness, or uncertainty. The term and the concept are used in diverse fields, from classical thermodynamics, where it was first recognized, to the microscopic description of nature in statistical physics, and to the principles of information theory. It has found far-ranging applications in chemistry and physics, in biological systems and their relation to life, in cosmology, economics, sociology, weather science, climate change, and information systems including the transmission of information in telecommunication. The thermodynamic concept was referred to by Scottish scientist and engineer William Rankine in 1850 with the names ''thermodynamic function'' and ''heat-potential''. In 1865, German physicist Rudolf Clausius, one of the leading founders of the field of thermodynamics, defined it as the quotient of an infinitesimal amount of hea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gibbs Free Energy
In thermodynamics, the Gibbs free energy (or Gibbs energy; symbol G) is a thermodynamic potential that can be used to calculate the maximum amount of work that may be performed by a thermodynamically closed system at constant temperature and pressure. It also provides a necessary condition for processes such as chemical reactions that may occur under these conditions. The Gibbs free energy change , measured in joules in SI) is the ''maximum'' amount of non-expansion work that can be extracted from a closed system (one that can exchange heat and work with its surroundings, but not matter) at fixed temperature and pressure. This maximum can be attained only in a completely reversible process. When a system transforms reversibly from an initial state to a final state under these conditions, the decrease in Gibbs free energy equals the work done by the system to its surroundings, minus the work of the pressure forces. The Gibbs energy is the thermodynamic potential that is minim ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Temperature
Temperature is a physical quantity that expresses quantitatively the perceptions of hotness and coldness. Temperature is measured with a thermometer. Thermometers are calibrated in various temperature scales that historically have relied on various reference points and thermometric substances for definition. The most common scales are the Celsius scale with the unit symbol °C (formerly called ''centigrade''), the Fahrenheit scale (°F), and the Kelvin scale (K), the latter being used predominantly for scientific purposes. The kelvin is one of the seven base units in the International System of Units (SI). Absolute zero, i.e., zero kelvin or −273.15 °C, is the lowest point in the thermodynamic temperature scale. Experimentally, it can be approached very closely but not actually reached, as recognized in the third law of thermodynamics. It would be impossible to extract energy as heat from a body at that temperature. Temperature is important in all fields of natur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pressure
Pressure (symbol: ''p'' or ''P'') is the force applied perpendicular to the surface of an object per unit area over which that force is distributed. Gauge pressure (also spelled ''gage'' pressure)The preferred spelling varies by country and even by industry. Further, both spellings are often used ''within'' a particular industry or country. Industries in British English-speaking countries typically use the "gauge" spelling. is the pressure relative to the ambient pressure. Various units are used to express pressure. Some of these derive from a unit of force divided by a unit of area; the SI unit of pressure, the pascal (Pa), for example, is one newton per square metre (N/m2); similarly, the pound-force per square inch (psi) is the traditional unit of pressure in the imperial and U.S. customary systems. Pressure may also be expressed in terms of standard atmospheric pressure; the atmosphere (atm) is equal to this pressure, and the torr is defined as of this. Manometric u ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differential Of A Function
In calculus, the differential represents the principal part of the change in a function ''y'' = ''f''(''x'') with respect to changes in the independent variable. The differential ''dy'' is defined by :dy = f'(x)\,dx, where f'(x) is the derivative of ''f'' with respect to ''x'', and ''dx'' is an additional real variable (so that ''dy'' is a function of ''x'' and ''dx''). The notation is such that the equation :dy = \frac\, dx holds, where the derivative is represented in the Leibniz notation ''dy''/''dx'', and this is consistent with regarding the derivative as the quotient of the differentials. One also writes :df(x) = f'(x)\,dx. The precise meaning of the variables ''dy'' and ''dx'' depends on the context of the application and the required level of mathematical rigor. The domain of these variables may take on a particular geometrical significance if the differential is regarded as a particular differential form, or analytical significance if the differential is re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phase Transition
In chemistry, thermodynamics, and other related fields, a phase transition (or phase change) is the physical process of transition between one state of a medium and another. Commonly the term is used to refer to changes among the basic states of matter: solid, liquid, and gas, and in rare cases, plasma. A phase of a thermodynamic system and the states of matter have uniform physical properties. During a phase transition of a given medium, certain properties of the medium change as a result of the change of external conditions, such as temperature or pressure. This can be a discontinuous change; for example, a liquid may become gas upon heating to its boiling point, resulting in an abrupt change in volume. The identification of the external conditions at which a transformation occurs defines the phase transition point. Types of phase transition At the phase transition point for a substance, for instance the boiling point, the two phases involved - liquid and vapor, have identic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |