|
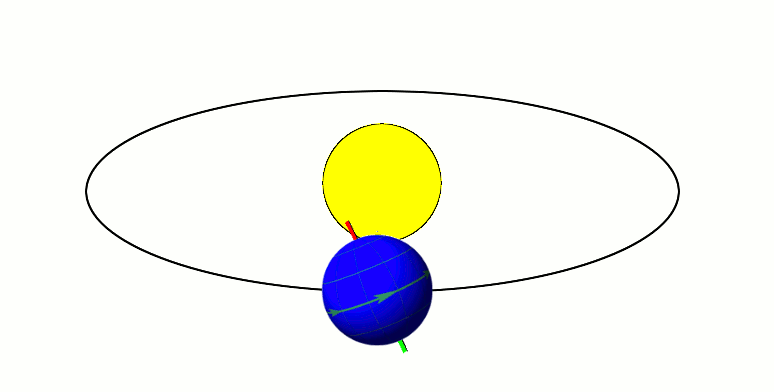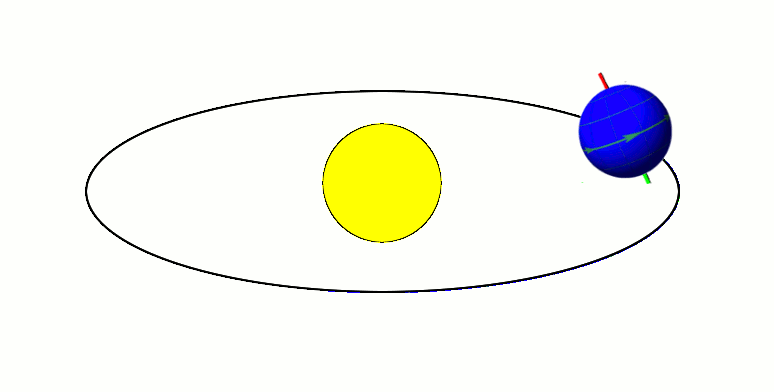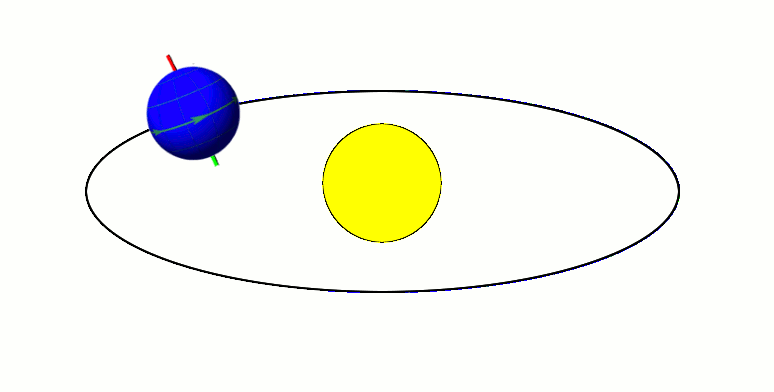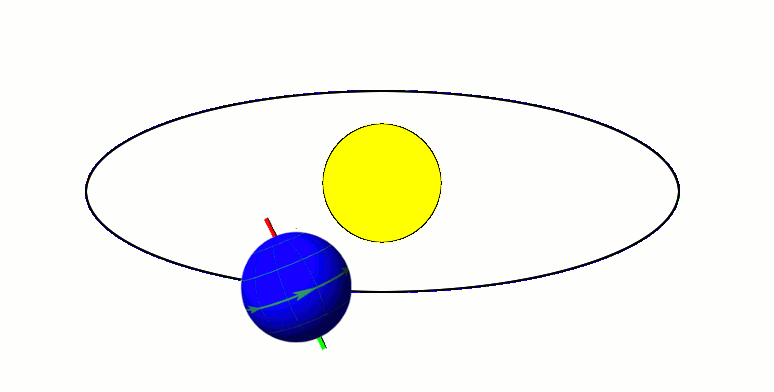
Earth-centered Inertial
Earth-centered inertial (ECI) coordinate frames have their origins at the center of mass of Earth and are fixed with respect to the stars. "I" in "ECI" stands for inertial (i.e. "not accelerating"), in contrast to the "Earth-centered - Earth-fixed" ( ECEF) frames, which remains fixed with respect to Earth's surface in its rotation, and then rotates with respect to stars. For objects in space, the equations of motion that describe orbital motion are simpler in a non-rotating frame such as ECI. The ECI frame is also useful for specifying the direction toward celestial objects: To represent the positions and velocities of terrestrial objects, it is convenient to use ECEF coordinates or latitude, longitude, and altitude. In a nutshell: * ECI: inertial, not rotating, with respect to the stars; useful to describe motion of celestial bodies and spacecraft. * ECEF: not inertial, accelerated, rotating w.r.t stars; useful to describe motion of objects on Earth surface. The ext ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Earth Centered Inertial Coordinate System
Earth is the third planet from the Sun and the only astronomical object known to harbor life. While large volumes of water can be found throughout the Solar System, only Earth sustains liquid surface water. About 71% of Earth's surface is made up of the ocean, dwarfing Earth's polar ice, lakes, and rivers. The remaining 29% of Earth's surface is land, consisting of continents and islands. Earth's surface layer is formed of several slowly moving tectonic plates, which interact to produce mountain ranges, volcanoes, and earthquakes. Earth's liquid outer core generates the magnetic field that shapes the magnetosphere of the Earth, deflecting destructive solar winds. The atmosphere of the Earth consists mostly of nitrogen and oxygen. Greenhouse gases in the atmosphere like carbon dioxide (CO2) trap a part of the energy from the Sun close to the surface. Water vapor is widely present in the atmosphere and forms clouds that cover most of the planet. More solar energy is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gravitational Field
In physics, a gravitational field is a model used to explain the influences that a massive body extends into the space around itself, producing a force on another massive body. Thus, a gravitational field is used to explain gravitational phenomena, and is measured in newtons per kilogram (N/kg). Equivalently, it is measured in meters per second squared (m/s2). In its original concept, gravity was a force between point masses. Following Isaac Newton, Pierre-Simon Laplace attempted to model gravity as some kind of radiation field or fluid, and since the 19th century, explanations for gravity have usually been taught in terms of a field model, rather than a point attraction. In a field model, rather than two particles attracting each other, the particles distort spacetime via their mass, and this distortion is what is perceived and measured as a "force". In such a model one states that matter moves in certain ways in response to the curvature of spacetime, and that there is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cartesian Coordinate System
A Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of numerical coordinates, which are the signed distances to the point from two fixed perpendicular oriented lines, measured in the same unit of length. Each reference coordinate line is called a ''coordinate axis'' or just ''axis'' (plural ''axes'') of the system, and the point where they meet is its ''origin'', at ordered pair . The coordinates can also be defined as the positions of the perpendicular projections of the point onto the two axes, expressed as signed distances from the origin. One can use the same principle to specify the position of any point in three-dimensional space by three Cartesian coordinates, its signed distances to three mutually perpendicular planes (or, equivalently, by its perpendicular projection onto three mutually perpendicular lines). In general, ''n'' Cartesian coordinates (an element of real ''n''-space) specify the point in an ' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geographic Coordinate System
The geographic coordinate system (GCS) is a spherical or ellipsoidal coordinate system for measuring and communicating positions directly on the Earth as latitude and longitude. It is the simplest, oldest and most widely used of the various spatial reference systems that are in use, and forms the basis for most others. Although latitude and longitude form a coordinate tuple like a cartesian coordinate system, the geographic coordinate system is not cartesian because the measurements are angles and are not on a planar surface. A full GCS specification, such as those listed in the EPSG and ISO 19111 standards, also includes a choice of geodetic datum (including an Earth ellipsoid), as different datums will yield different latitude and longitude values for the same location. History The invention of a geographic coordinate system is generally credited to Eratosthenes of Cyrene, who composed his now-lost ''Geography'' at the Library of Alexandria in the 3rd century ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spherical Coordinate System
In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a point is specified by three numbers: the ''radial distance'' of that point from a fixed origin, its ''polar angle'' measured from a fixed zenith direction, and the ''azimuthal angle'' of its orthogonal projection on a reference plane that passes through the origin and is orthogonal to the zenith, measured from a fixed reference direction on that plane. It can be seen as the three-dimensional version of the polar coordinate system. The radial distance is also called the ''radius'' or ''radial coordinate''. The polar angle may be called '' colatitude'', ''zenith angle'', '' normal angle'', or ''inclination angle''. When radius is fixed, the two angular coordinates make a coordinate system on the sphere sometimes called spherical polar coordinates. The use of symbols and the order of the coordinates differs among sources and disciplines. This article will us ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
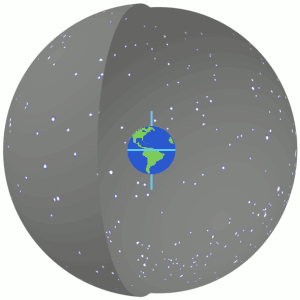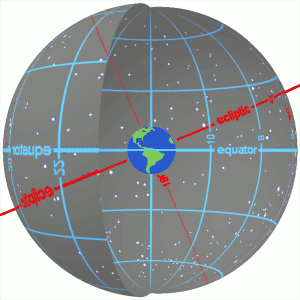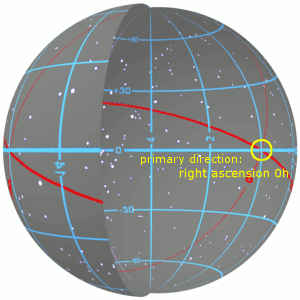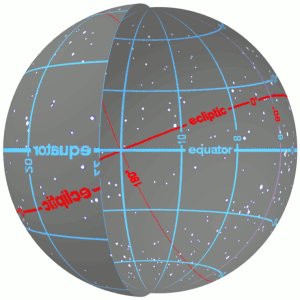
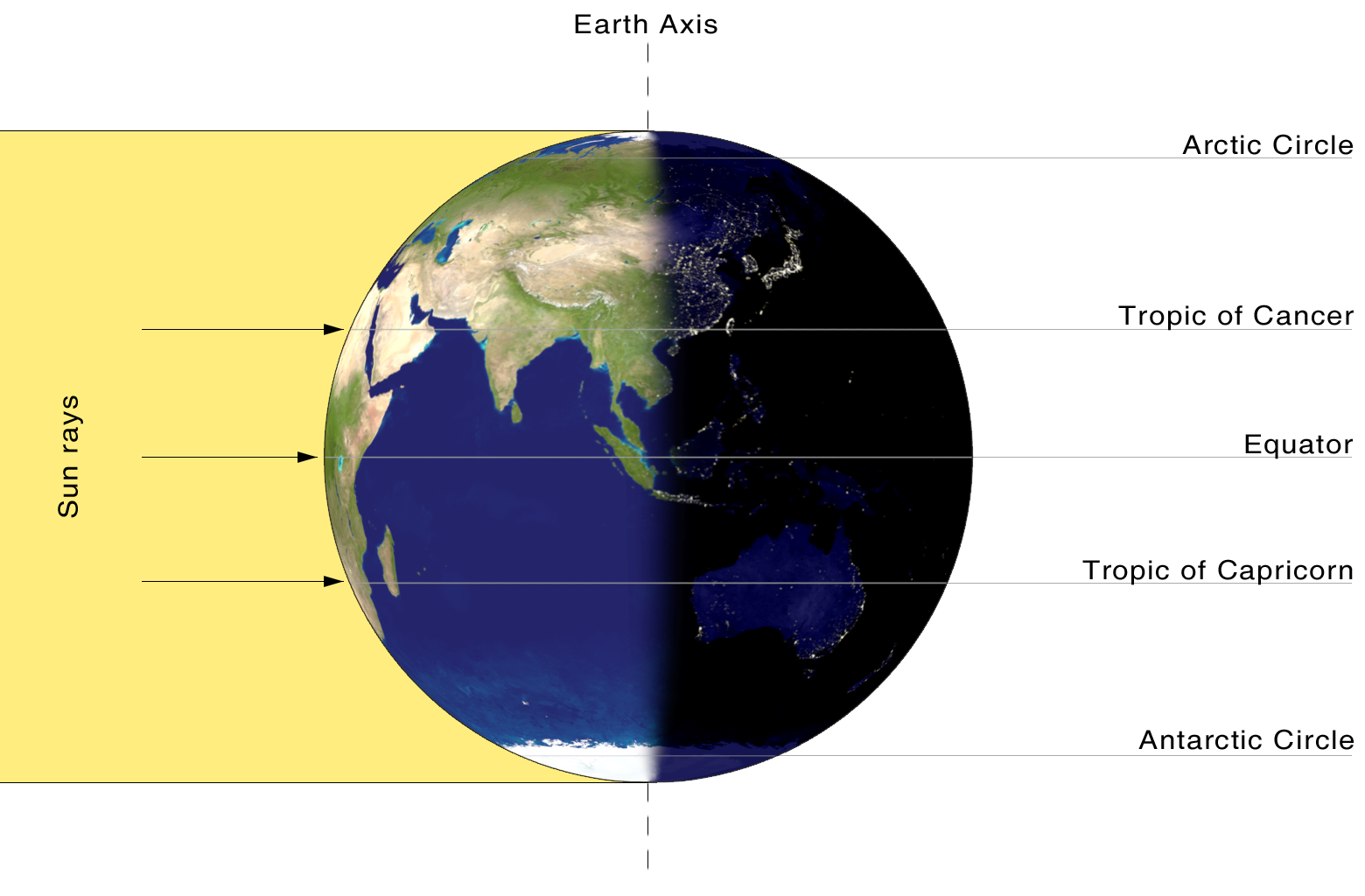
Celestial Equator
The celestial equator is the great circle of the imaginary celestial sphere on the same plane as the equator of Earth. This plane of reference bases the equatorial coordinate system. In other words, the celestial equator is an abstract projection of the terrestrial equator into outer space. Due to Earth's axial tilt, the celestial equator is currently inclined by about 23.44° with respect to the ecliptic (the plane of Earth's orbit), but has varied from about 22.0° to 24.5° over the past 5 million years due to perturbation from other planets. An observer standing on Earth's equator visualizes the celestial equator as a semicircle passing through the zenith, the point directly overhead. As the observer moves north (or south), the celestial equator tilts towards the opposite horizon. The celestial equator is defined to be infinitely distant (since it is on the celestial sphere); thus, the ends of the semicircle always intersect the horizon due east and due west, regardless ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Declination
In astronomy, declination (abbreviated dec; symbol ''δ'') is one of the two angles that locate a point on the celestial sphere in the equatorial coordinate system, the other being hour angle. Declination's angle is measured north or south of the celestial equator, along the hour circle passing through the point in question. The root of the word ''declination'' (Latin, ''declinatio'') means "a bending away" or "a bending down". It comes from the same root as the words ''incline'' ("bend foward") and ''recline'' ("bend backward"). In some 18th and 19th century astronomical texts, declination is given as ''North Pole Distance'' (N.P.D.), which is equivalent to 90 – (declination). For instance an object marked as declination −5 would have an N.P.D. of 95, and a declination of −90 (the south celestial pole) would have an N.P.D. of 180. Explanation Declination in astronomy is comparable to geographic latitude, projected onto the celestial sphere, and right ascension is like ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Right Ascension
Right ascension (abbreviated RA; symbol ) is the angular distance of a particular point measured eastward along the celestial equator from the Sun at the March equinox to the (hour circle of the) point in question above the earth. When paired with declination, these astronomical coordinates specify the location of a point on the celestial sphere in the equatorial coordinate system. An old term, ''right ascension'' ( la, ascensio recta), "''Ascensio recta'' Solis, stellæ, aut alterius cujusdam signi, est gradus æquatorus cum quo simul exoritur in sphæra recta"; roughly translated, "''Right ascension'' of the Sun, stars, or any other sign, is the degree of the equator that rises together in a right sphere" refers to the ''ascension'', or the point on the celestial equator that rises with any celestial object as seen from Earth's equator, where the celestial equator intersects the horizon at a right angle. It contrasts with ''oblique ascension'', the point on the celestial ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fundamental Plane (spherical Coordinates)
The fundamental plane in a spherical coordinate system is a plane of reference that divides the sphere into two hemispheres. The geocentric latitude of a point is then the angle between the fundamental plane and the line joining the point to the centre of the sphere. For a geographic coordinate system of the Earth, the fundamental plane is the Equator. Astronomical coordinate systems have varying fundamental planes: * The horizontal coordinate system uses the observer's horizon. * The Besselian coordinate system uses Earth's terminator (day/night boundary). This is a Cartesian coordinate system (''x'', ''y'', ''z''). * The equatorial coordinate system uses the celestial equator. * The ecliptic coordinate system uses the ecliptic. * The galactic coordinate system uses the Milky Way's galactic equator. See also *Plane of reference In celestial mechanics, the plane of reference (or reference plane) is the plane used to define orbital elements (positions). The two main orbital ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
March Equinox
The March equinox or northward equinox is the equinox on the Earth when the subsolar point appears to leave the Southern Hemisphere and cross the celestial equator, heading northward as seen from Earth. The March equinox is known as the vernal equinox (spring equinox) in the Northern Hemisphere and as the autumnal equinox in the Southern Hemisphere. On the Gregorian calendar, the northward equinox can occur as early as 19 March or as late as 21 March at 0° longitude. For a common year the computed time slippage is about 5 hours 49 minutes ''later'' than the previous year, and for a leap year about 18 hours 11 minutes ''earlier'' than the previous year. Balancing the increases of the common years against the losses of the leap years keeps the calendar date of the March equinox from drifting more than one day from 20 March each year. The March equinox may be taken to mark the beginning of astronomical spring and the end of astronomical winter in the Northern Hemisphere but m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equinox
A solar equinox is a moment in time when the Sun crosses the Earth's equator, which is to say, appears directly above the equator, rather than north or south of the equator. On the day of the equinox, the Sun appears to rise "due east" and set "due west". This occurs twice each year, around 20 March and 23 September. More precisely, an equinox is traditionally defined as the time when the plane of Earth's equator passes through the geometric center of the Sun's disk. Equivalently, this is the moment when Earth's rotation axis is directly perpendicular to the Sun-Earth line, tilting neither toward nor away from the Sun. In modern times, since the Moon (and to a lesser extent the planets) causes Earth's orbit to vary slightly from a perfect ellipse, the equinox is officially defined by the Sun's more regular ecliptic longitude rather than by its declination. The instants of the equinoxes are currently defined to be when the apparent geocentric longitude of the Sun is 0° a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Obliquity
In astronomy, axial tilt, also known as obliquity, is the angle between an object's rotational axis and its orbital axis, which is the line perpendicular to its orbital plane; equivalently, it is the angle between its equatorial plane and orbital plane. It differs from orbital inclination. At an obliquity of 0 degrees, the two axes point in the same direction; that is, the rotational axis is perpendicular to the orbital plane. The rotational axis of Earth, for example, is the imaginary line that passes through both the North Pole and South Pole, whereas the Earth's orbital axis is the line perpendicular to the imaginary plane through which the Earth moves as it revolves around the Sun; the Earth's obliquity or axial tilt is the angle between these two lines. Earth's obliquity oscillates between 22.1 and 24.5 degrees on a 41,000-year cycle. Based on a continuously updated formula (here Laskar, 1986, though since 2006 the IMCCE and the IAU recommend the P03 model), Earth's mean ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |