|
Equipotential
In mathematics and physics, an equipotential or isopotential refers to a region in space where every point is at the same potential. This usually refers to a scalar potential (in that case it is a level set of the potential), although it can also be applied to vector potentials. An equipotential of a scalar potential function in - dimensional space is typically an ()-dimensional space. The del operator illustrates the relationship between a vector field and its associated scalar potential field. An equipotential region might be referred as being 'of equipotential' or simply be called 'an equipotential'. An equipotential region of a scalar potential in three-dimensional space is often an equipotential surface (or ''potential isosurface''), but it can also be a three-dimensional mathematical solid in space. The gradient of the scalar potential (and hence also its opposite, as in the case of a vector field with an associated potential field) is everywhere perpendicular to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equipotential By Zureks
In mathematics and physics, an equipotential or isopotential refers to a region in space where every point is at the same potential. This usually refers to a scalar potential (in that case it is a level set of the potential), although it can also be applied to vector potentials. An equipotential of a scalar potential function in -dimensional space is typically an ()-dimensional space. The del operator illustrates the relationship between a vector field and its associated scalar potential field. An equipotential region might be referred as being 'of equipotential' or simply be called 'an equipotential'. An equipotential region of a scalar potential in three-dimensional space is often an equipotential surface (or ''potential isosurface''), but it can also be a three-dimensional mathematical solid in space. The gradient of the scalar potential (and hence also its opposite, as in the case of a vector field with an associated potential field) is everywhere perpendicular to the equ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scalar Potential
In mathematical physics, scalar potential, simply stated, describes the situation where the difference in the potential energies of an object in two different positions depends only on the positions, not upon the path taken by the object in traveling from one position to the other. It is a scalar field in three-space: a directionless value ( scalar) that depends only on its location. A familiar example is potential energy due to gravity. A ''scalar potential'' is a fundamental concept in vector analysis and physics (the adjective ''scalar'' is frequently omitted if there is no danger of confusion with ''vector potential''). The scalar potential is an example of a scalar field. Given a vector field , the scalar potential is defined such that: : \mathbf = -\nabla P = - \left( \frac, \frac, \frac \right), where is the gradient of and the second part of the equation is minus the gradient for a function of the Cartesian coordinates . In some cases, mathematicians may use a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Level Set
In mathematics, a level set of a real-valued function of real variables is a set where the function takes on a given constant value , that is: : L_c(f) = \left\~, When the number of independent variables is two, a level set is called a level curve, also known as '' contour line'' or ''isoline''; so a level curve is the set of all real-valued solutions of an equation in two variables and . When , a level set is called a level surface (or '' isosurface''); so a level surface is the set of all real-valued roots of an equation in three variables , and . For higher values of , the level set is a level hypersurface, the set of all real-valued roots of an equation in variables. A level set is a special case of a fiber. Alternative names Level sets show up in many applications, often under different names. For example, an implicit curve is a level curve, which is considered independently of its neighbor curves, emphasizing that such a curve is defined by an impl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electric Current
An electric current is a stream of charged particles, such as electrons or ions, moving through an electrical conductor or space. It is measured as the net rate of flow of electric charge through a surface or into a control volume. The moving particles are called charge carriers, which may be one of several types of particles, depending on the conductor. In electric circuits the charge carriers are often electrons moving through a wire. In semiconductors they can be electrons or holes. In an electrolyte the charge carriers are ions, while in plasma, an ionized gas, they are ions and electrons. The SI unit of electric current is the ampere, or ''amp'', which is the flow of electric charge across a surface at the rate of one coulomb per second. The ampere (symbol: A) is an SI base unit. Electric current is measured using a device called an ammeter. Electric currents create magnetic fields, which are used in motors, generators, inductors, and transformers. In ordi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Potential Gradient
In physics, chemistry and biology, a potential gradient is the local rate of change of the potential with respect to displacement, i.e. spatial derivative, or gradient. This quantity frequently occurs in equations of physical processes because it leads to some form of flux. Definition One dimension The simplest definition for a potential gradient ''F'' in one dimension is the following: : F = \frac = \frac\,\! where is some type of scalar potential and is displacement (not distance) in the direction, the subscripts label two different positions , and potentials at those points, . In the limit of infinitesimal displacements, the ratio of differences becomes a ratio of differentials: : F = \frac.\,\! The direction of the electric potential gradient is from x_1 to x_2. Three dimensions In three dimensions, Cartesian coordinates make it clear that the resultant potential gradient is the sum of the potential gradients in each direction: : \mathbf = \mathbf_x\frac + \mat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Potential Flow
In fluid dynamics, potential flow (or ideal flow) describes the velocity field as the gradient of a scalar function: the velocity potential. As a result, a potential flow is characterized by an irrotational velocity field, which is a valid approximation for several applications. The irrotationality of a potential flow is due to the curl of the gradient of a scalar always being equal to zero. In the case of an incompressible flow the velocity potential satisfies Laplace's equation, and potential theory is applicable. However, potential flows also have been used to describe compressible flows. The potential flow approach occurs in the modeling of both stationary as well as nonstationary flows. Applications of potential flow are for instance: the outer flow field for aerofoils, water waves, electroosmotic flow, and groundwater flow. For flows (or parts thereof) with strong vorticity effects, the potential flow approximation is not applicable. Characteristics and applications ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
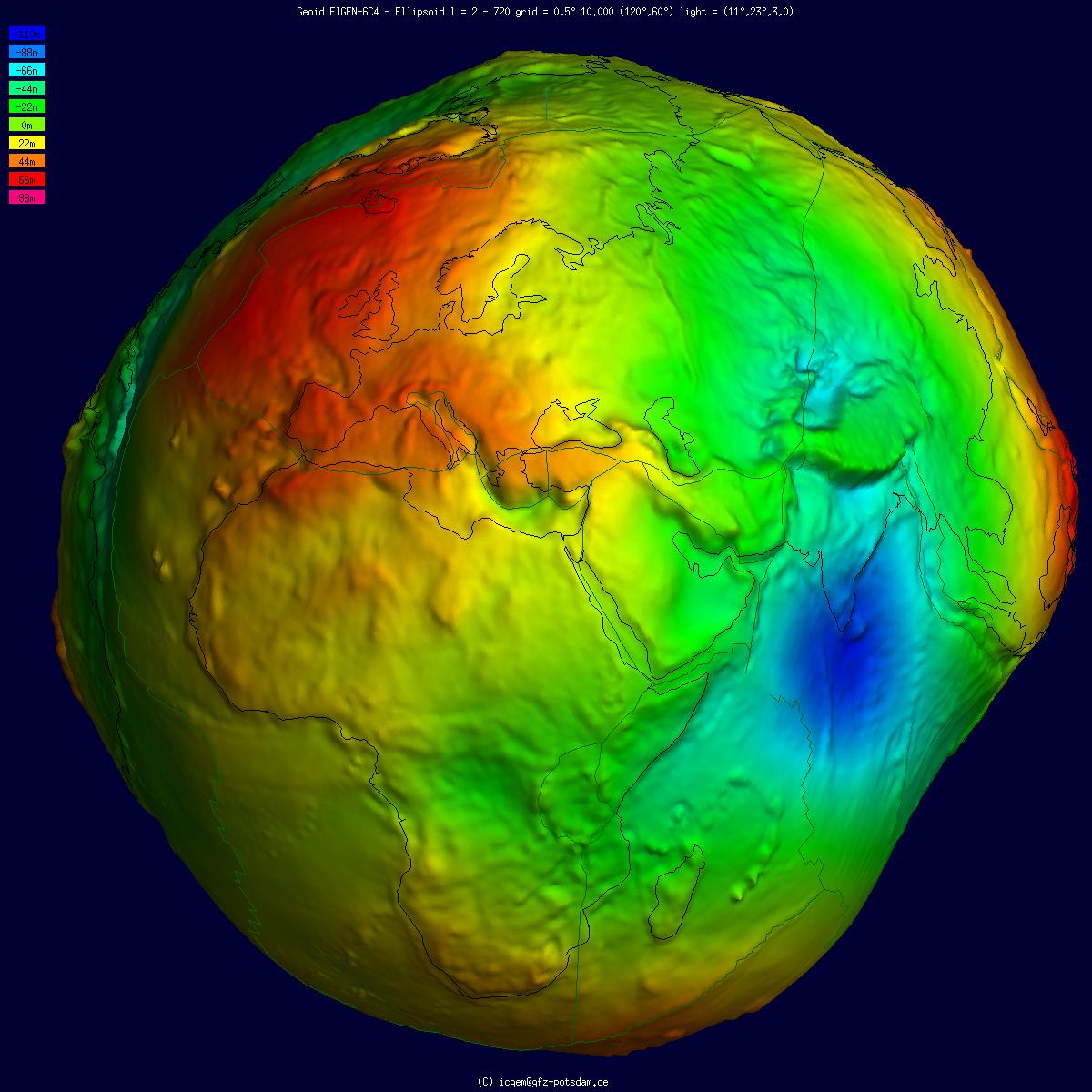
Geoid
The geoid () is the shape that the ocean surface would take under the influence of the gravity of Earth, including gravitational attraction and Earth's rotation, if other influences such as winds and tides were absent. This surface is extended through the continents (such as with very narrow hypothetical canals). According to Gauss, who first described it, it is the "mathematical figure of the Earth", a smooth but irregular surface whose shape results from the uneven distribution of mass within and on the surface of Earth. It can be known only through extensive gravitational measurements and calculations. Despite being an important concept for almost 200 years in the history of geodesy and geophysics, it has been defined to high precision only since advances in satellite geodesy in the late 20th century. All points on a geoid surface have the same geopotential (the sum of gravitational potential energy and centrifugal potential energy). The force of gravity acts everywher ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mean Sea Level
There are several kinds of mean in mathematics, especially in statistics. Each mean serves to summarize a given group of data, often to better understand the overall value ( magnitude and sign) of a given data set. For a data set, the '' arithmetic mean'', also known as "arithmetic average", is a measure of central tendency of a finite set of numbers: specifically, the sum of the values divided by the number of values. The arithmetic mean of a set of numbers ''x''1, ''x''2, ..., x''n'' is typically denoted using an overhead bar, \bar. If the data set were based on a series of observations obtained by sampling from a statistical population, the arithmetic mean is the '' sample mean'' (\bar) to distinguish it from the mean, or expected value, of the underlying distribution, the '' population mean'' (denoted \mu or \mu_x).Underhill, L.G.; Bradfield d. (1998) ''Introstat'', Juta and Company Ltd.p. 181/ref> Outside probability and statistics, a wide range of other notions of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geopotential
Geopotential is the potential of the Earth's gravity field. For convenience it is often defined as the ''negative'' of the potential energy per unit mass, so that the gravity vector is obtained as the gradient of this potential, without the negation. In addition to the actual potential (the geopotential), a hypothetical normal potential and their difference, the disturbing potential, can also be defined. Concept For geophysical applications, gravity is distinguished from gravitation. Gravity is defined as the resultant force of gravitation and the centrifugal force caused by the Earth's rotation. Likewise, the respective scalar potentials can be added to form an effective potential called the geopotential, W. Global mean sea surface is close to one of the isosurfaces of the geopotential. This ''equipotential surface'', or surface of constant geopotential, is called the ''geoid''. How the gravitational force and the centrifugal force add up to a force orthogonal to the geoid is ill ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gravity Of Earth
The gravity of Earth, denoted by , is the net acceleration that is imparted to objects due to the combined effect of gravitation (from mass distribution within Earth) and the centrifugal force (from the Earth's rotation). It is a vector quantity, whose direction coincides with a plumb bob and strength or magnitude is given by the norm g=\, \mathit\, . In SI units this acceleration is expressed in metres per second squared (in symbols, m/ s2 or m·s−2) or equivalently in newtons per kilogram (N/kg or N·kg−1). Near Earth's surface, the gravity acceleration is approximately , which means that, ignoring the effects of air resistance, the speed of an object falling freely will increase by about per second every second. This quantity is sometimes referred to informally as ''little '' (in contrast, the gravitational constant is referred to as ''big ''). The precise strength of Earth's gravity varies depending on location. The nominal "average" value at Earth's surface ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Horizontal Plane
In astronomy, geography, and related sciences and contexts, a '' direction'' or '' plane'' passing by a given point is said to be vertical if it contains the local gravity direction at that point. Conversely, a direction or plane is said to be horizontal if it is perpendicular to the vertical direction. In general, something that is vertical can be drawn from up to down (or down to up), such as the y-axis in the Cartesian coordinate system. Historical definition The word ''horizontal'' is derived from the Latin , which derives from the Greek , meaning 'separating' or 'marking a boundary'. The word ''vertical'' is derived from the late Latin ', which is from the same root as ''vertex'', meaning 'highest point' or more literally the 'turning point' such as in a whirlpool. Girard Desargues defined the vertical to be perpendicular to the horizon in his 1636 book ''Perspective''. Geophysical definition The plumb line and spirit level In physics, engineering and construction, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Faraday Cage
A Faraday cage or Faraday shield is an enclosure used to block electromagnetic fields. A Faraday shield may be formed by a continuous covering of conductive material, or in the case of a Faraday cage, by a mesh of such materials. Faraday cages are named after scientist Michael Faraday, who invented them in 1836. A Faraday cage operates because an external electrical field causes the electric charges within the cage's conducting material to be distributed so that they cancel the field's effect in the cage's interior. This phenomenon is used to protect sensitive electronic equipment (for example RF receivers) from external radio frequency interference (RFI) often during testing or alignment of the device. They are also used to protect people and equipment against actual electric currents such as lightning strikes and electrostatic discharges, since the enclosing cage conducts current around the outside of the enclosed space and none passes through the interior. Faraday cages ca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |