|
Equidistant Conic Projection
The equidistant conic projection is a conic map projection commonly used for maps of small countries as well as for larger regions such as the continental United States that are elongated east-to-west. Also known as the simple conic projection, a rudimentary version was described during the 2nd century CE by the Greek astronomer and geographer Ptolemy in his work ''Geography''. The projection has the useful property that distances along the meridians are proportionately correct, and distances are also correct along two standard parallels that the mapmaker has chosen. The two standard parallels are also free of distortion. For maps of regions elongated east-to-west (such as the continental United States) the standard parallels are chosen to be about a sixth of the way inside the northern and southern limits of interest. This way distortion is minimized throughout the region of interest. Transformation Coordinates from a spherical datum can be transformed to an equidistant conic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equidistant Conic Projection SW
A point is said to be equidistant from a set of objects if the distances between that point and each object in the set are equal. In two-dimensional Euclidean geometry, the locus of points equidistant from two given (different) points is their perpendicular bisector. In three dimensions, the locus of points equidistant from two given points is a plane, and generalising further, in n-dimensional space the locus of points equidistant from two points in ''n''-space is an (''n''−1)-space. For a triangle the circumcentre is a point equidistant from each of the three vertices. Every non-degenerate triangle has such a point. This result can be generalised to cyclic polygons: the circumcentre is equidistant from each of the vertices. Likewise, the incentre of a triangle or any other tangential polygon is equidistant from the points of tangency of the polygon's sides with the circle. Every point on a perpendicular bisector of the side of a triangle or other polygon is equidi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
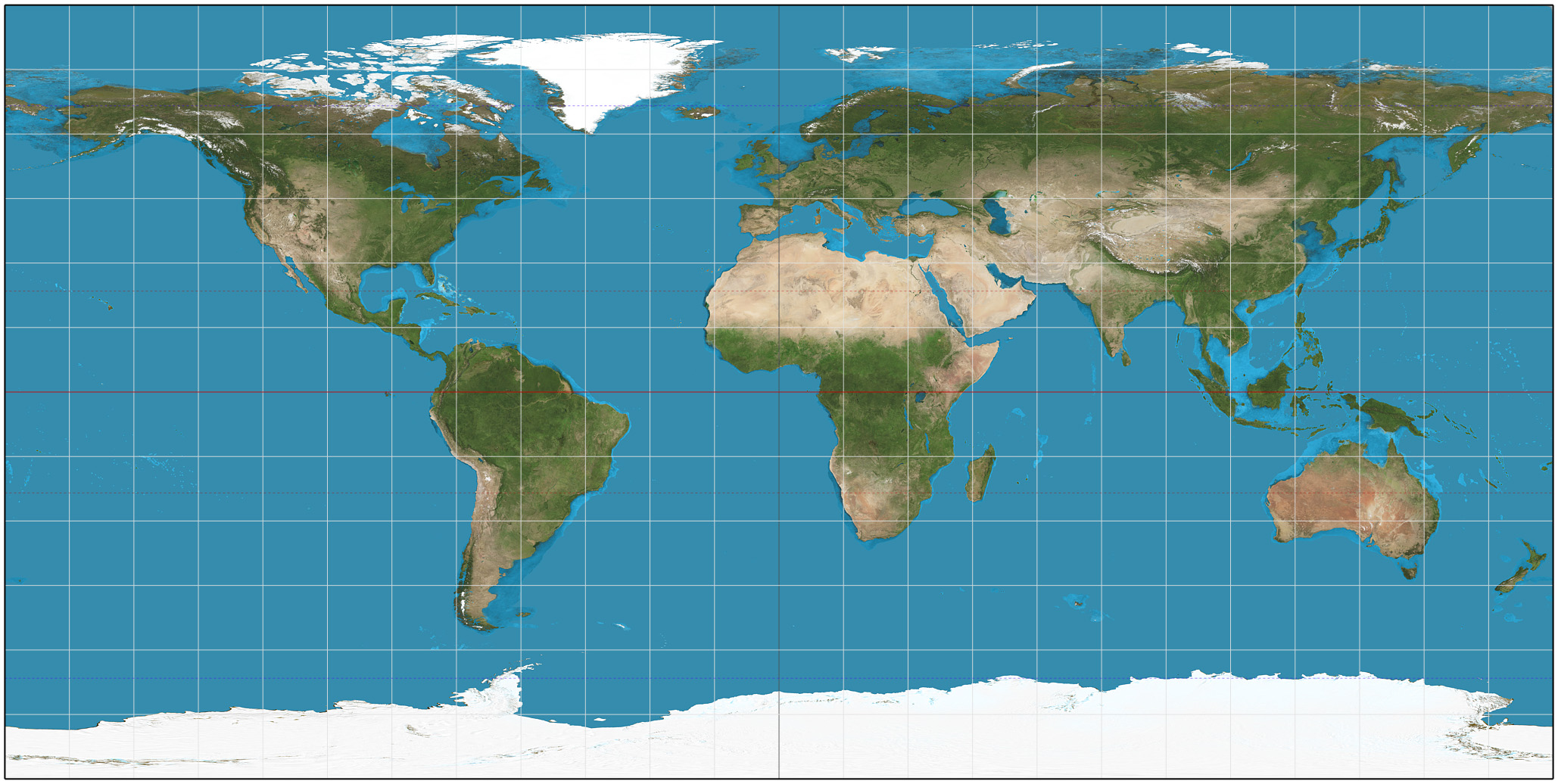
Map Projection
In cartography, a map projection is any of a broad set of Transformation (function) , transformations employed to represent the curved two-dimensional Surface (mathematics), surface of a globe on a Plane (mathematics), plane. In a map projection, coordinates, often expressed as latitude and longitude, of locations from the surface of the globe are transformed to coordinates on a plane. Projection is a necessary step in creating a two-dimensional map and is one of the essential elements of cartography. All projections of a sphere on a plane necessarily distort the surface in some way. Depending on the purpose of the map, some distortions are acceptable and others are not; therefore, different map projections exist in order to preserve some properties of the sphere-like body at the expense of other properties. The study of map projections is primarily about the characterization of their distortions. There is no limit to the number of possible map projections. More generally, proje ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ptolemy
Claudius Ptolemy (; , ; ; – 160s/170s AD) was a Greco-Roman mathematician, astronomer, astrologer, geographer, and music theorist who wrote about a dozen scientific treatises, three of which were important to later Byzantine science, Byzantine, Islamic science, Islamic, and Science in the Renaissance, Western European science. The first was his astronomical treatise now known as the ''Almagest'', originally entitled ' (, ', ). The second is the ''Geography (Ptolemy), Geography'', which is a thorough discussion on maps and the geographic knowledge of the Greco-Roman world. The third is the astrological treatise in which he attempted to adapt horoscopic astrology to the Aristotelian physics, Aristotelian natural philosophy of his day. This is sometimes known as the ' (, 'On the Effects') but more commonly known as the ' (from the Koine Greek meaning 'four books'; ). The Catholic Church promoted his work, which included the only mathematically sound geocentric model of the Sola ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geography (Ptolemy)
The ''Geography'' (, , "Geographical Guidance"), also known by its Latin names as the ' and the ', is a gazetteer, an atlas (book), atlas, and a treatise on cartography, compiling the geographical knowledge of the 2nd-century Roman Empire. Originally written by Claudius Ptolemy in Ancient Greek, Greek at Alexandria around 150 AD, the work was a revision of a now-lost atlas by Marinus of Tyre using additional Roman and Parthian Empire, Persian gazetteers and new principles. Its translation – Al-Khwarizmi#Geography, Kitab Surat al-Ard – into Classical Arabic, Arabic by Al-Khwarizmi, Al-Khwarismi in the 9th century was highly influential on the geographical knowledge and cartographic traditions of the Geography and cartography in medieval Islam, Islamic world. Alongside the works of Islamic scholars – and the commentary containing revised and more accurate data by Alfraganus – Ptolemy's work was subsequently highly influential on Middle Ages, Medieval and Renaissanc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Datum (geodesy)
A geodetic datum or geodetic system (also: geodetic reference datum, geodetic reference system, or geodetic reference frame, or terrestrial reference frame) is a global datum reference or reference frame for unambiguously representing the position of locations on Earth by means of either geodetic coordinates (and related vertical coordinates) or geocentric coordinates. DatumsThe plural is not "data" in this case are crucial to any technology or technique based on spatial location, including geodesy, navigation, surveying, geographic information systems, remote sensing, and cartography. A horizontal datum is used to measure a horizontal position, across the Earth's surface, in latitude and longitude or another related coordinate system. A ''vertical datum'' is used to measure the elevation or depth relative to a standard origin, such as mean sea level (MSL). A three-dimensional datum enables the expression of both horizontal and vertical position components in a unified form. Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cartesian Coordinate System
In geometry, a Cartesian coordinate system (, ) in a plane (geometry), plane is a coordinate system that specifies each point (geometry), point uniquely by a pair of real numbers called ''coordinates'', which are the positive and negative numbers, signed distances to the point from two fixed perpendicular oriented lines, called ''coordinate lines'', ''coordinate axes'' or just ''axes'' (plural of ''axis'') of the system. The point where the axes meet is called the ''Origin (mathematics), origin'' and has as coordinates. The axes direction (geometry), directions represent an orthogonal basis. The combination of origin and basis forms a coordinate frame called the Cartesian frame. Similarly, the position of any point in three-dimensional space can be specified by three ''Cartesian coordinates'', which are the signed distances from the point to three mutually perpendicular planes. More generally, Cartesian coordinates specify the point in an -dimensional Euclidean space for any di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Map Projections
This is a summary of map projections that have articles of their own on Wikipedia or that are otherwise WP:NOTABLE, notable. Because there is no limit to the number of possible map projections, there can be no comprehensive list. Table of projections *The first known popularizer/user and not necessarily the creator. Key Type of projection surface ; Cylindrical: In normal aspect, these map regularly-spaced meridians to equally spaced vertical lines, and parallels to horizontal lines. ; Pseudocylindrical: In normal aspect, these map the central meridian and parallels as straight lines. Other meridians are curves (or possibly straight from pole to equator), regularly spaced along parallels. ; Conic: In normal aspect, conic (or conical) projections map meridians as straight lines, and parallels as arcs of circles. ; Pseudoconical: In normal aspect, pseudoconical projections represent the central meridian as a straight line, other meridians as complex curves, and parallels as ci ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |