|
Equations Of State Calculations By Fast Computing Machines
"Equation of State Calculations by Fast Computing Machines" is a scholarly article published by Nicholas Metropolis, Arianna W. Rosenbluth, Marshall N. Rosenbluth, Augusta H. Teller, and Edward Teller in the Journal of Chemical Physics in 1953. This paper proposed what became known as the Metropolis Monte Carlo algorithm, which forms the basis for Monte Carlo statistical mechanics simulations of atomic and molecular systems. Development Some controversy exists with regard to credit for development of the algorithm. Prior to 2003, there was no detailed account of the algorithm's development. Then, shortly before his death, Marshall Rosenbluth attended a 2003 conference at LANL marking the 50th anniversary of the 1953 publication. At this conference, Rosenbluth described the algorithm and its development in a presentation titled "Genesis of the Monte Carlo Algorithm for Statistical Mechanics". Further historical clarification is made by Gubernatis in a 2005 journal article rec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scholarly Article
Academic publishing is the subfield of publishing which distributes academic research and scholarship. Most academic work is published in academic journal articles, books or theses. The part of academic written output that is not formally published but merely printed up or posted on the Internet is often called "grey literature". Most scientific and scholarly journals, and many academic and scholarly books, though not all, are based on some form of peer review or editorial refereeing to qualify texts for publication. Peer review quality and selectivity standards vary greatly from journal to journal, publisher to publisher, and field to field. Most established academic disciplines have their own journals and other outlets for publication, although many academic journals are somewhat interdisciplinary, and publish work from several distinct fields or subfields. There is also a tendency for existing journals to divide into specialized sections as the field itself becomes more spec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boltzmann Factor
Factor, a Latin word meaning "who/which acts", may refer to: Commerce * Factor (agent), a person who acts for, notably a mercantile and colonial agent * Factor (Scotland), a person or firm managing a Scottish estate * Factors of production, such a factor is a resource used in the production of goods and services Science and technology Biology * Coagulation factors, substances essential for blood coagulation * Environmental factor, any abiotic or biotic factor that affects life * Enzyme, proteins that catalyze chemical reactions * Factor B, and factor D, peptides involved in the alternate pathway of immune system complement activation * Transcription factor, a protein that binds to specific DNA sequences Computer science and information technology * Factor (programming language), a concatenative stack-oriented programming language * Factor (Unix), a utility for factoring an integer into its prime factors * Factor, a substring, a subsequence of consecutive symbols in a s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Torus
In geometry, a torus (plural tori, colloquially donut or doughnut) is a surface of revolution generated by revolving a circle in three-dimensional space about an axis that is coplanar with the circle. If the axis of revolution does not touch the circle, the surface has a ring shape and is called a torus of revolution. If the axis of revolution is tangent to the circle, the surface is a horn torus. If the axis of revolution passes twice through the circle, the surface is a spindle torus. If the axis of revolution passes through the center of the circle, the surface is a degenerate torus, a double-covered sphere. If the revolved curve is not a circle, the surface is called a ''toroid'', as in a square toroid. Real-world objects that approximate a torus of revolution include swim rings, inner tubes and ringette rings. Eyeglass lenses that combine spherical and cylindrical correction are toric lenses. A torus should not be confused with a '' solid torus'', which is formed by r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
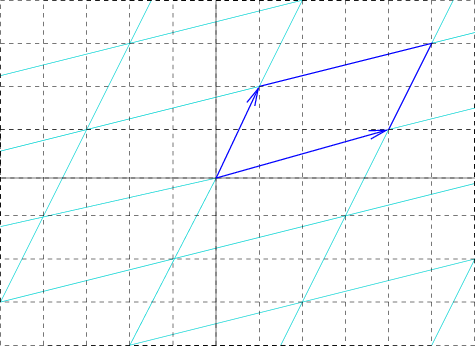
Unit Cell
In geometry, biology, mineralogy and solid state physics, a unit cell is a repeating unit formed by the vectors spanning the points of a lattice. Despite its suggestive name, the unit cell (unlike a unit vector, for example) does not necessarily have unit size, or even a particular size at all. Rather, the primitive cell is the closest analogy to a unit vector, since it has a determined size for a given lattice and is the basic building block from which larger cells are constructed. The concept is used particularly in describing crystal structure in two and three dimensions, though it makes sense in all dimensions. A lattice can be characterized by the geometry of its unit cell, which is a section of the tiling (a parallelogram or parallelepiped) that generates the whole tiling using only translations. There are two special cases of the unit cell: the primitive cell and the conventional cell. The primitive cell is a unit cell corresponding to a single lattice point, it is the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Periodic Boundary Conditions
Periodic boundary conditions (PBCs) are a set of boundary conditions which are often chosen for approximating a large (infinite) system by using a small part called a ''unit cell''. PBCs are often used in computer simulations and mathematical models. The topology of two-dimensional PBC is equal to that of a ''world map'' of some video games; the geometry of the unit cell satisfies perfect two-dimensional tiling, and when an object passes through one side of the unit cell, it re-appears on the opposite side with the same velocity. In topological terms, the space made by two-dimensional PBCs can be thought of as being mapped onto a torus (compactification). The large systems approximated by PBCs consist of an infinite number of unit cells. In computer simulations, one of these is the original simulation box, and others are copies called ''images''. During the simulation, only the properties of the original simulation box need to be recorded and propagated. The ''minimum-image conventi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Los Alamos National Lab
Los Alamos National Laboratory (often shortened as Los Alamos and LANL) is one of the sixteen research and development laboratories of the United States Department of Energy (DOE), located a short distance northwest of Santa Fe, New Mexico, in the American southwest. Best known for its central role in helping develop the first atomic bomb, LANL is one of the world's largest and most advanced scientific institutions. Los Alamos was established in 1943 as Project Y, a top-secret site for designing nuclear weapons under the Manhattan Project during World War II.The site was variously called Los Alamos Laboratory and Los Alamos Scientific Laboratory. Chosen for its remote yet relatively accessible location, it served as the main hub for conducting and coordinating nuclear research, bringing together some of the world's most famous scientists, among them numerous Nobel Prize winners. The town of Los Alamos, directly north of the lab, grew extensively through this period. After ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
MANIAC
Maniac (from Greek μανιακός, ''maniakos'') is a pejorative for an individual who experiences the mood known as mania. In common usage, it is also an insult for someone involved in reckless behavior. Maniac may also refer to: Film * ''Maniac'' (1934 film), an exploitation film directed by Dwain Esper * ''Maniac'' (1963 film), directed by Michael Carreras *''The Ransom'' (aka ''Maniac!''), 1977 film with Oliver Reed * ''Maniac'' (1980 film), directed by William Lustig * ''Maniac'' (2011 film), directed by Shia LaBeouf * ''Maniac'' (2012 film), a remake of the 1980 film Literature * ''Maniac'', a 1995 novel by John Peel Television * ''Maniac'' (Norwegian TV series), a Norwegian television series * ''Maniac'' (miniseries), an American TV series based on the Norwegian series Medicine * Melanocytic nevus with intraepidermal ascent of cells Games *'' Ideal Maniac'', a handheld electronic LED game created by the Ideal Toy Company Music * Maniac (producer), grime produ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lennard-Jones Potential
The Lennard-Jones potential (also termed the LJ potential or 12-6 potential) is an intermolecular pair potential. Out of all the intermolecular potentials, the Lennard-Jones potential is probably the one that has been the most extensively studied. It is considered an archetype model for simple yet realistic intermolecular interactions. The Lennard-Jones potential models soft repulsive and attractive ( van der Waals) interactions. Hence, the Lennard-Jones potential describes electronically neutral atoms or molecules. It is named after John Lennard-Jones. The commonly used expression for the Lennard-Jones potential is V_\text(r) = 4\varepsilon \left \left(\frac\right)^ - \left(\frac\right)^6 \right, where r is the distance between two interacting particles, \varepsilon is the depth of the potential well (usually referred to as 'dispersion energy'), and \sigma is the distance at which the particle-particle potential energy V is zero (often referred to as 'size of the particle'). The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rigid Sphere
Hard spheres are widely used as model particles in the statistical mechanical theory of fluids and solids. They are defined simply as impenetrable spheres that cannot overlap in space. They mimic the extremely strong ("infinitely elastic bouncing") repulsion that atoms and spherical molecules experience at very close distances. Hard spheres systems are studied by analytical means, by molecular dynamics simulations, and by the experimental study of certain colloidal model systems. The hard-sphere system provides a generic model that explains the quasiuniversal structure and dynamics of simple liquids. Formal definition Hard spheres of diameter \sigma are particles with the following pairwise interaction potential: :V(\mathbf_1,\mathbf_2)=\left\{ \begin{matrix}0 & \mbox{if}\quad , \mathbf{r}_1-\mathbf{r}_2, \geq \sigma \\ \infty & \mbox{if}\quad, \mathbf{r}_1-\mathbf{r}_2, < \sigma \end{matrix} \right. where and are th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equation Of State
In physics, chemistry, and thermodynamics, an equation of state is a thermodynamic equation relating state variables, which describe the state of matter under a given set of physical conditions, such as pressure, volume, temperature, or internal energy. Most modern equations of state are formulated in the Helmholtz free energy. Equations of state are useful in describing the properties of pure substances and mixtures in liquids, gases, and solid states as well as the state of matter in the interior of stars. Overview At present, there is no single equation of state that accurately predicts the properties of all substances under all conditions. An example of an equation of state correlates densities of gases and liquids to temperatures and pressures, known as the ideal gas law, which is roughly accurate for weakly polar gases at low pressures and moderate temperatures. This equation becomes increasingly inaccurate at higher pressures and lower temperatures, and fails to predict ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Limit Of A Sequence
As the positive integer n becomes larger and larger, the value n\cdot \sin\left(\tfrac1\right) becomes arbitrarily close to 1. We say that "the limit of the sequence n\cdot \sin\left(\tfrac1\right) equals 1." In mathematics, the limit of a sequence is the value that the terms of a sequence "tend to", and is often denoted using the \lim symbol (e.g., \lim_a_n).Courant (1961), p. 29. If such a limit exists, the sequence is called convergent. A sequence that does not converge is said to be divergent. The limit of a sequence is said to be the fundamental notion on which the whole of mathematical analysis ultimately rests. Limits can be defined in any metric or topological space, but are usually first encountered in the real numbers. History The Greek philosopher Zeno of Elea is famous for formulating paradoxes that involve limiting processes. Leucippus, Democritus, Antiphon, Eudoxus, and Archimedes developed the method of exhaustion, which uses an infinite sequence of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
