|
Elliptic Tiling
In geometry, a (globally) projective polyhedron is a tessellation of the real projective plane. These are projective analogs of spherical polyhedra – tessellations of the sphere – and toroidal polyhedra – tessellations of the toroids. Projective polyhedra are also referred to as elliptic tessellations or elliptic tilings, referring to the projective plane as (projective) elliptic geometry, by analogy with spherical tiling, a synonym for "spherical polyhedron". However, the term elliptic geometry applies to both spherical and projective geometries, so the term carries some ambiguity for polyhedra. As CW complex, cellular decompositions of the projective plane, they have Euler characteristic 1, while spherical polyhedra have Euler characteristic 2. The qualifier "globally" is to contrast with ''locally'' projective polyhedra, which are #Generalizations, defined in the theory of abstract polyhedra. Non-overlapping projective polyhedra (density (polytope), density 1) correspond ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is called a ''geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point, line, plane, distance, angle, surface, and curve, as fundamental concepts. During the 19th century several discoveries enlarged dramatically the scope of geometry. One of the oldest such discoveries is Carl Friedrich Gauss' ("remarkable theorem") that asserts roughly that the Gaussian curvature of a surface is independent from any specific embedding in a Euclidean space. This implies that surfaces can be studied ''intrinsically'', that is, as stand-alone spaces, and has been expanded into the theory of manifolds and Riemannian geometry. Later in the 19th century, it appeared that geome ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Relation With Traditional Polyhedra
Relation or relations may refer to: General uses *International relations, the study of interconnection of politics, economics, and law on a global level *Interpersonal relationship, association or acquaintance between two or more people *Public relations, managing the spread of information to the public *Sexual relations, or human sexual activity *Social relation, in social science, any social interaction between two or more individuals Logic and philosophy * Relation (philosophy), links between properties of an object *Relational theory, framework to understand reality or a physical system Mathematics A finitary or ''n''-ary relation is a set of ''n''-tuples. Specific types of relations include: *Relation (mathematics) * Binary relation (or correspondence, dyadic relation, or 2-place relation) * Equivalence relation *Homogeneous relation *Reflexive relation *Serial relation *Ternary relation (or triadic, 3-adic, 3-ary, 3-dimensional, or 3-place relation) Relation may also ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uniform Polyhedra
In geometry, a uniform polyhedron has regular polygons as faces and is vertex-transitive (i.e., there is an isometry mapping any vertex onto any other). It follows that all vertices are congruent. Uniform polyhedra may be regular (if also face- and edge-transitive), quasi-regular (if also edge-transitive but not face-transitive), or semi-regular (if neither edge- nor face-transitive). The faces and vertices need not be convex, so many of the uniform polyhedra are also star polyhedra. There are two infinite classes of uniform polyhedra, together with 75 other polyhedra: *Infinite classes: **prisms, **antiprisms. * Convex exceptional: ** 5 Platonic solids: regular convex polyhedra, ** 13 Archimedean solids: 2 quasiregular and 11 semiregular convex polyhedra. * Star (nonconvex) exceptional: ** 4 Kepler–Poinsot polyhedra: regular nonconvex polyhedra, ** 53 uniform star polyhedra: 14 quasiregular and 39 semiregular. Hence 5 + 13 + 4 + 53 = 75. There are also many degen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hemipolyhedra
In geometry, a hemipolyhedron is a uniform star polyhedron some of whose faces pass through its center. These "hemi" faces lie parallel to the faces of some other symmetrical polyhedron, and their count is half the number of faces of that other polyhedron – hence the "hemi" prefix. The prefix "hemi" is also used to refer to certain projective polyhedra, such as the hemi-cube, which are the image of a 2 to 1 map of a spherical polyhedron with central symmetry. Wythoff symbol and vertex figure Their Wythoff symbols are of the form ''p''/(''p'' − ''q'') ''p''/''q'' , ''r''; their vertex figures are crossed quadrilaterals. They are thus related to the cantellated polyhedra, which have similar Wythoff symbols. The vertex configuration is ''p''/''q''.2''r''.''p''/(''p'' − ''q'').2''r''. The 2''r''-gon faces pass through the center of the model: if represented as faces of spherical polyhedra, they cover an entire hemisphere and the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tetrahemihexahedron
In geometry, the tetrahemihexahedron or hemicuboctahedron is a uniform star polyhedron, indexed as U4. It has 7 faces (4 triangles and 3 squares), 12 edges, and 6 vertices. Its vertex figure is a crossed quadrilateral. Its Coxeter–Dynkin diagram is (although this is a double covering of the tetrahemihexahedron). It is the only non-prismatic uniform polyhedron with an odd number of faces. Its Wythoff symbol is 3/2 3 , 2, but that represents a double covering of the tetrahemihexahedron with eight triangles and six squares, paired and coinciding in space. (It can more intuitively be seen as two coinciding tetrahemihexahedra.) It is a hemipolyhedron. The "hemi" part of the name means some of the faces form a group with half as many members as some regular polyhedron—here, three square faces form a group with half as many faces as the regular hexahedron, better known as the cube—hence ''hemihexahedron''. Hemi faces are also oriented in the same direction as the regular poly ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Antipodal Map
In mathematics, antipodal points of a sphere are those diametrically opposite to each other (the specific qualities of such a definition are that a line drawn from the one to the other passes through the center of the sphere so forms a true diameter). This term applies to opposite points on a circle or any n-sphere. An antipodal point is sometimes called an antipode, a back-formation from the Greek loan word ''antipodes'', meaning "opposite (the) feet", as the true word singular is ''antipus''. Theory In mathematics, the concept of ''antipodal points'' is generalized to spheres of any dimension: two points on the sphere are antipodal if they are opposite ''through the centre''; for example, taking the centre as origin, they are points with related vectors v and −v. On a circle, such points are also called diametrically opposite. In other words, each line through the centre intersects the sphere in two points, one for each ray out from the centre, and these two points ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
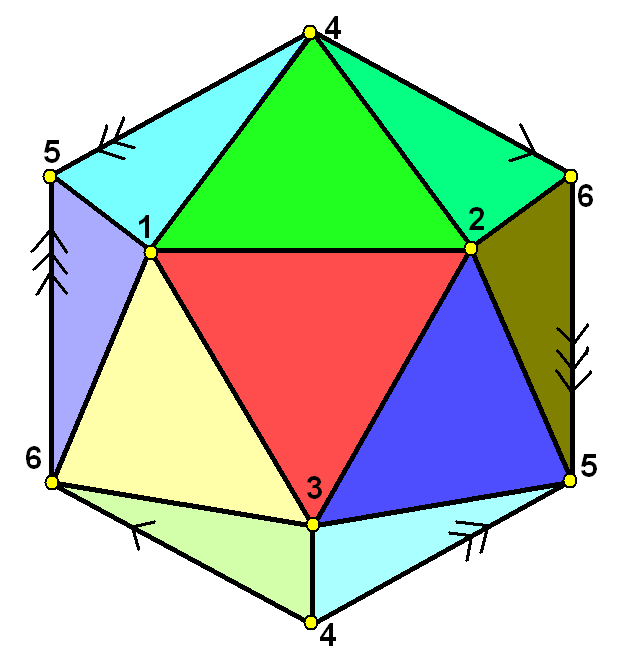
Hemi-icosahedron
A hemi-icosahedron is an abstract regular polyhedron, containing half the faces of a regular icosahedron. It can be realized as a projective polyhedron (a tessellation of the real projective plane by 10 triangles), which can be visualized by constructing the projective plane as a hemisphere where opposite points along the boundary are connected and dividing the hemisphere into three equal parts. Geometry It has 10 triangular faces, 15 edges, and 6 vertices. It is also related to the nonconvex uniform polyhedron, the tetrahemihexahedron, which could be topologically identical to the hemi-icosahedron if each of the 3 square faces were divided into two triangles. Graphs It can be represented symmetrically on faces, and vertices as Schlegel diagrams: The complete graph K6 It has the same vertices and edges as the 5-dimensional 5-simplex which has a complete graph of edges, but only contains half of the (20) faces. From the point of view of graph theory this is an embedding o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hemi-dodecahedron
A hemi-dodecahedron is an abstract regular polyhedron, containing half the faces of a regular dodecahedron. It can be realized as a projective polyhedron (a tessellation of the real projective plane by 6 pentagons), which can be visualized by constructing the projective plane as a hemisphere where opposite points along the boundary are connected and dividing the hemisphere into three equal parts. It has 6 pentagonal faces, 15 edges, and 10 vertices. Projections It can be projected symmetrically inside of a 10-sided or 12-sided perimeter: : Petersen graph From the point of view of graph theory this is an embedding of the Petersen graph on a real projective plane. With this embedding, the dual graph is ''K''6 (the complete graph with 6 vertices) --- see hemi-icosahedron. See also * 57-cell – an abstract regular 4-polytope constructed from 57 hemi-dodecahedra. *hemi-icosahedron A hemi-icosahedron is an abstract regular polyhedron, containing half the faces of a regular icosah ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hemi-octahedron
A hemi-octahedron is an abstract regular polyhedron, containing half the faces of a regular octahedron. It has 4 triangular faces, 6 edges, and 3 vertices. Its dual polyhedron is the hemicube. It can be realized as a projective polyhedron (a tessellation of the real projective plane by 4 triangles), which can be visualized by constructing the projective plane as a hemisphere where opposite points along the boundary are connected and dividing the hemisphere into four equal parts. It can be seen as a square pyramid without its base. It can be represented symmetrically as a hexagonal or square Schlegel diagram: : It has an unexpected property that there are two distinct edges between every pair of vertices – any two vertices define a digon. See also *Hemi-dodecahedron *Hemi-icosahedron A hemi-icosahedron is an abstract regular polyhedron, containing half the faces of a regular icosahedron. It can be realized as a projective polyhedron (a tessellation of the real projectiv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hemicube (geometry)
In abstract geometry, a hemicube is an abstract, regular polyhedron, containing half the faces of a cube. Realization It can be realized as a projective polyhedron (a tessellation of the real projective plane by three quadrilaterals), which can be visualized by constructing the projective plane as a hemisphere where opposite points along the boundary are connected and dividing the hemisphere into three equal parts. It has three square faces, six edges, and four vertices. It has an unexpected property that every face is in contact with every other face on two edges, and every face contains all the vertices, which gives an example of an abstract polytope whose faces are not determined by their vertex sets. From the point of view of graph theory the skeleton is a tetrahedral graph, an embedding of ''K''4 (the complete graph with four vertices) on a projective plane. The hemicube should not be confused with the demicube – the hemicube is a projective polyhedron, while the demic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hosohedra
In spherical geometry, an -gonal hosohedron is a tessellation of lunes on a spherical surface, such that each lune shares the same two polar opposite vertices. A regular -gonal hosohedron has Schläfli symbol with each spherical lune having internal angle radians ( degrees). Hosohedra as regular polyhedra For a regular polyhedron whose Schläfli symbol is , the number of polygonal faces is : :N_2=\frac. The Platonic solids known to antiquity are the only integer solutions for ''m'' ≥ 3 and ''n'' ≥ 3. The restriction ''m'' ≥ 3 enforces that the polygonal faces must have at least three sides. When considering polyhedra as a spherical tiling, this restriction may be relaxed, since digons (2-gons) can be represented as spherical lunes, having non-zero area. Allowing ''m'' = 2 makes :N_2=\frac=n, and admits a new infinite class of regular polyhedra, which are the hosohedra. On a spherical surface, the polyhedron is represented as ''n'' abutting lunes, with interio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dihedra
A dihedron is a type of polyhedron, made of two polygon faces which share the same set of ''n'' edges. In three-dimensional Euclidean space, it is degenerate if its faces are flat, while in three-dimensional spherical space, a dihedron with flat faces can be thought of as a lens, an example of which is the fundamental domain of a lens space L(''p'',''q''). Dihedra have also been called bihedra, flat polyhedra, or doubly covered polygons. As a spherical tiling, a dihedron can exist as nondegenerate form, with two ''n''-sided faces covering the sphere, each face being a hemisphere, and vertices on a great circle. It is regular if the vertices are equally spaced. The dual of an ''n''-gonal dihedron is an ''n''-gonal hosohedron, where ''n'' digon faces share two vertices. As a flat-faced polyhedron A dihedron can be considered a degenerate prism whose two (planar) ''n''-sided polygon bases are connected "back-to-back", so that the resulting object has no depth. The polygons must ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |