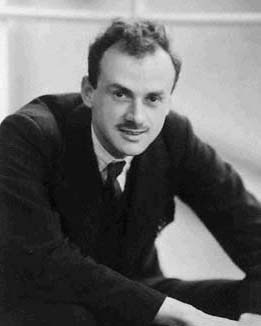|
Electron Spin
In atomic physics, the electron magnetic moment, or more specifically the electron magnetic dipole moment, is the magnetic moment of an electron resulting from its intrinsic properties of spin (physics), spin and electric charge. The value of the electron magnetic moment is The electron magnetic moment has been measured to an accuracy of relative to the Bohr magneton. Magnetic moment of an electron The electron is a charged particle with charge −, where is the elementary charge, unit of elementary charge. Its angular momentum comes from two types of rotation: Spin (physics), spin and orbital motion. From classical electrodynamics, a rotating distribution of electric charge produces a magnetic dipole, so that it behaves like a tiny bar magnet. One consequence is that an external magnetic field exerts a Magnetic moment#Torque on a moment, torque on the electron magnetic moment that depends on the orientation of this dipole with respect to the field. If the electron is visuali ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electron Spin Resonance
Electron paramagnetic resonance (EPR) or electron spin resonance (ESR) spectroscopy is a method for studying materials that have unpaired electrons. The basic concepts of EPR are analogous to those of nuclear magnetic resonance (NMR), but the spins excited are those of the electrons instead of the atomic nuclei. EPR spectroscopy is particularly useful for studying metal complexes and organic radicals. EPR was first observed in Kazan State University by Soviet physicist Yevgeny Zavoisky in 1944, and was developed independently at the same time by Brebis Bleaney at the University of Oxford. Theory Origin of an EPR signal Every electron has a magnetic moment and spin quantum number s = \tfrac , with magnetic components m_\mathrm = + \tfrac or m_\mathrm = - \tfrac . In the presence of an external magnetic field with strength B_\mathrm , the electron's magnetic moment aligns itself either antiparallel ( m_\mathrm = - \tfrac ) or parallel ( m_\mathrm = + \tfrac ) to the fi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rest Mass
The invariant mass, rest mass, intrinsic mass, proper mass, or in the case of bound systems simply mass, is the portion of the total mass of an object or system of objects that is independent of the overall motion of the system. More precisely, it is a characteristic of the system's total energy and momentum that is the same in all frames of reference related by Lorentz transformations.Lawrence S. LernerPhysics for Scientists and Engineers, Volume 2, page 1073 1997. If a center-of-momentum frame exists for the system, then the invariant mass of a system is equal to its total mass in that "rest frame". In other reference frames, where the system's momentum is nonzero, the total mass (a.k.a. relativistic mass) of the system is greater than the invariant mass, but the invariant mass remains unchanged. Because of mass–energy equivalence, the rest energy of the system is simply the invariant mass times the speed of light squared. Similarly, the total energy of the system is its total ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Electrodynamics
In particle physics, quantum electrodynamics (QED) is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved. QED mathematically describes all phenomena involving electrically charged particles interacting by means of exchange of photons and represents the quantum counterpart of classical electromagnetism giving a complete account of matter and light interaction. In technical terms, QED can be described as a perturbation theory of the electromagnetic quantum vacuum. Richard Feynman called it "the jewel of physics" for its extremely accurate predictions of quantities like the anomalous magnetic moment of the electron and the Lamb shift of the energy levels of hydrogen. History The first formulation of a quantum theory describing radiation and matter interaction is attributed to British scientist Paul Dirac, who ( ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Anomalous Magnetic Dipole Moment
In quantum electrodynamics, the anomalous magnetic moment of a particle is a contribution of effects of quantum mechanics, expressed by Feynman diagrams with loops, to the magnetic moment of that particle. (The ''magnetic moment'', also called ''magnetic dipole moment'', is a measure of the strength of a magnetic source.) The "Dirac" magnetic moment, corresponding to tree-level Feynman diagrams (which can be thought of as the classical result), can be calculated from the Dirac equation. It is usually expressed in terms of the ''g''-factor; the Dirac equation predicts g = 2. For particles such as the electron, this classical result differs from the observed value by a small fraction of a percent. The difference is the anomalous magnetic moment, denoted a and defined as a = \frac Electron The one-loop contribution to the anomalous magnetic moment—corresponding to the first and largest quantum mechanical correction—of the electron is found by calculating the vertex functio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Antiparallel (mathematics)
In geometry, antiparallel lines (or anti-parallel lines) can be defined with respect to either lines or angles. Definitions Given two lines m_1 and m_2, lines l_1 and l_2 are antiparallel with respect to m_1 and m_2 if \angle 1 = \angle 2, as shown in Fig.1. If l_1 and l_2 are antiparallel with respect to m_1 and m_2, then m_1 and m_2 are also antiparallel with respect to l_1 and l_2. In any quadrilateral inscribed in a circle, any two opposite sides are antiparallel with respect to the other two sides (Fig.2). Two lines l_1 and l_2 are antiparallel with respect to the sides of an angle if and only if they make the same angle \angle APC in the opposite senses with the bisector of that angle (Fig.3). Antiparallel vectors In a Euclidean space, two directed line segments, often called ''vectors'' in applied mathematics, are antiparallel if they are supported by parallel lines and have opposite directions.Chapter 6, p. 332 In that case, one of the associated Euclidean vectors is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spin Quantum Number
In atomic physics, the spin quantum number is a quantum number (designated ) which describes the intrinsic angular momentum (or spin angular momentum, or simply spin) of an electron or other particle. The phrase was originally used to describe the fourth of a set of quantum numbers (the principal quantum number , the azimuthal quantum number , the magnetic quantum number , and the spin quantum number ), which completely describe the quantum state of an electron in an atom. The name comes from a physical spinning of the electron about an axis, as proposed by Uhlenbeck and Goudsmit. The value of is the component of spin angular momentum parallel to a given direction (the –axis), which can be either +1/2 or –1/2 (in units of the reduced Planck constant). However this simplistic picture was quickly realized to be physically impossible because it would require the electrons to rotate faster than the speed of light. It was therefore replaced by a more abstract quantum-mechanical ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Anapole Moment
A toroidal moment is an independent term in the multipole expansion of electromagnetic fields besides magnetic and electric multipoles. In the electrostatic multipole expansion, all charge and current distributions can be expanded into a complete set of electric and magnetic multipole coefficients. However, additional terms arise in an electrodynamic multipole expansion. The coefficients of these terms are given by the toroidal multipole moments as well as time derivatives of the electric and magnetic multipole moments. While electric dipoles can be understood as separated charges and magnetic dipoles as circular currents, axial (or electric) toroidal dipoles describes toroidal charge arrangements whereas polar (or magnetic) toroidal dipole (also called anapole) correspond to the field of a solenoid bent into a torus. Classical toroidal dipole moment A complex expression allows the current density J to be written as a sum of electric, magnetic, and toroidal moments using Cart ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electron Electric Dipole Moment
The electron electric dipole moment is an intrinsic property of an electron such that the potential energy is linearly related to the strength of the electric field: :U = \mathbf d_ \cdot \mathbf E. The electron's electric dipole moment (EDM) must be collinear with the direction of the electron's magnetic moment (spin). Within the Standard Model of elementary particle physics, such a dipole is predicted to be non-zero but very small, at most , where ''e'' stands for the elementary charge. The discovery of a substantially larger electron electric dipole moment would imply a violation of both parity invariance and time reversal invariance. Implications for Standard Model and extensions In the Standard Model, the electron EDM arises from the CP-violating components of the CKM matrix. The moment is very small because the CP violation involves quarks, not electrons directly, so it can only arise by quantum processes where virtual quarks are created, interact with the electron, an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dirac Equation
In particle physics, the Dirac equation is a relativistic wave equation derived by British physicist Paul Dirac in 1928. In its free form, or including electromagnetic interactions, it describes all spin- massive particles, called "Dirac particles", such as electrons and quarks for which parity is a symmetry. It is consistent with both the principles of quantum mechanics and the theory of special relativity, and was the first theory to account fully for special relativity in the context of quantum mechanics. It was validated by accounting for the fine structure of the hydrogen spectrum in a completely rigorous way. The equation also implied the existence of a new form of matter, ''antimatter'', previously unsuspected and unobserved and which was experimentally confirmed several years later. It also provided a ''theoretical'' justification for the introduction of several component wave functions in Pauli's phenomenological theory of spin. The wave functions in the Dirac theo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Form Factor (quantum Field Theory)
In elementary particle physics and mathematical physics, in particular in effective field theory, a form factor is a function that encapsulates the properties of a certain particle interaction without including all of the underlying physics, but instead, providing the momentum dependence of suitable matrix elements. It is further measured experimentally in confirmation or specification of a theory—see experimental particle physics. Photon–nucleon example For example, at low energies the interaction of a photon with a nucleon is a very complicated calculation involving interactions between the photon and a sea of quarks and gluons, and often the calculation cannot be fully performed from first principles. Often in this context, form factors are also called "structure functions", since they can be used to describe the structure of the nucleon. However, the generic Lorentz-invariant form of the matrix element for the electromagnetic current interaction is known, : \varepsilo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angular Momentum Quantum Number
The azimuthal quantum number is a quantum number for an atomic orbital that determines its orbital angular momentum and describes the shape of the orbital. The azimuthal quantum number is the second of a set of quantum numbers that describe the unique quantum state of an electron (the others being the principal quantum number, the magnetic quantum number, and the spin quantum number). It is also known as the orbital angular momentum quantum number, orbital quantum number or second quantum number, and is symbolized as ℓ (pronounced ''ell''). Derivation Connected with the energy states of the atom's electrons are four quantum numbers: ''n'', ''ℓ'', ''m''''ℓ'', and ''m''''s''. These specify the complete, unique quantum state of a single electron in an atom, and make up its wavefunction or ''orbital''. When solving to obtain the wave function, the Schrödinger equation reduces to three equations that lead to the first three quantum numbers. Therefore, the equations for the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reduced Planck Constant
The Planck constant, or Planck's constant, is a fundamental physical constant of foundational importance in quantum mechanics. The constant gives the relationship between the energy of a photon and its frequency, and by the mass-energy equivalence, the relationship between mass and frequency. Specifically, a photon's energy is equal to its frequency multiplied by the Planck constant. The constant is generally denoted by h. The reduced Planck constant, or Dirac constant, equal to the constant divided by 2 \pi, is denoted by \hbar. In metrology it is used, together with other constants, to define the kilogram, the SI unit of mass. The SI units are defined in such a way that, when the Planck constant is expressed in SI units, it has the exact value The constant was first postulated by Max Planck in 1900 as part of a solution to the ultraviolet catastrophe. At the end of the 19th century, accurate measurements of the spectrum of black body radiation existed, but the distribut ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |