|
Elastic Moduli
An elastic modulus (also known as modulus of elasticity (MOE)) is a quantity that describes an object's or substance's resistance to being deformed elastically (i.e., non-permanently) when a stress is applied to it. Definition The elastic modulus of an object is defined as the slope of its stress–strain curve in the elastic deformation region: A stiffer material will have a higher elastic modulus. An elastic modulus has the form: :\delta \ \stackrel\ \frac where stress is the force causing the deformation divided by the area to which the force is applied and strain is the ratio of the change in some parameter caused by the deformation to the original value of the parameter. Since strain is a dimensionless quantity, the units of \delta will be the same as the units of stress. Elastic constants and moduli Elastic constants are specific parameters that quantify the stiffness of a material in response to applied stresses and are fundamental in defining the elastic prop ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stress (mechanics)
In continuum mechanics, stress is a physical quantity that describes forces present during deformation. For example, an object being pulled apart, such as a stretched elastic band, is subject to ''tensile'' stress and may undergo elongation. An object being pushed together, such as a crumpled sponge, is subject to ''compressive'' stress and may undergo shortening. The greater the force and the smaller the cross-sectional area of the body on which it acts, the greater the stress. Stress has dimension of force per area, with SI units of newtons per square meter (N/m2) or pascal (Pa). Stress expresses the internal forces that neighbouring particles of a continuous material exert on each other, while ''strain'' is the measure of the relative deformation of the material. For example, when a solid vertical bar is supporting an overhead weight, each particle in the bar pushes on the particles immediately below it. When a liquid is in a closed container under pressure, each ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bulk Modulus
The bulk modulus (K or B or k) of a substance is a measure of the resistance of a substance to bulk compression. It is defined as the ratio of the infinitesimal pressure increase to the resulting ''relative'' decrease of the volume. Other moduli describe the material's response ( strain) to other kinds of stress: the shear modulus describes the response to shear stress, and Young's modulus describes the response to normal (lengthwise stretching) stress. For a fluid, only the bulk modulus is meaningful. For a complex anisotropic solid such as wood or paper, these three moduli do not contain enough information to describe its behaviour, and one must use the full generalized Hooke's law. The reciprocal of the bulk modulus at fixed temperature is called the isothermal compressibility. Definition The bulk modulus K (which is usually positive) can be formally defined by the equation :K=-V\frac , where P is pressure, V is the initial volume of the substance, and dP/dV deno ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Crystal Structure
In crystallography, crystal structure is a description of ordered arrangement of atoms, ions, or molecules in a crystalline material. Ordered structures occur from intrinsic nature of constituent particles to form symmetric patterns that repeat along the principal directions of three-dimensional space in matter. The smallest group of particles in a material that constitutes this repeating pattern is the unit cell of the structure. The unit cell completely reflects the symmetry and structure of the entire crystal, which is built up by repetitive translation of the unit cell along its principal axes. The translation vectors define the nodes of the Bravais lattice. The lengths of principal axes/edges, of the unit cell and angles between them are lattice constants, also called ''lattice parameters'' or ''cell parameters''. The symmetry properties of a crystal are described by the concept of space groups. All possible symmetric arrangements of particles in three-dimensional space ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
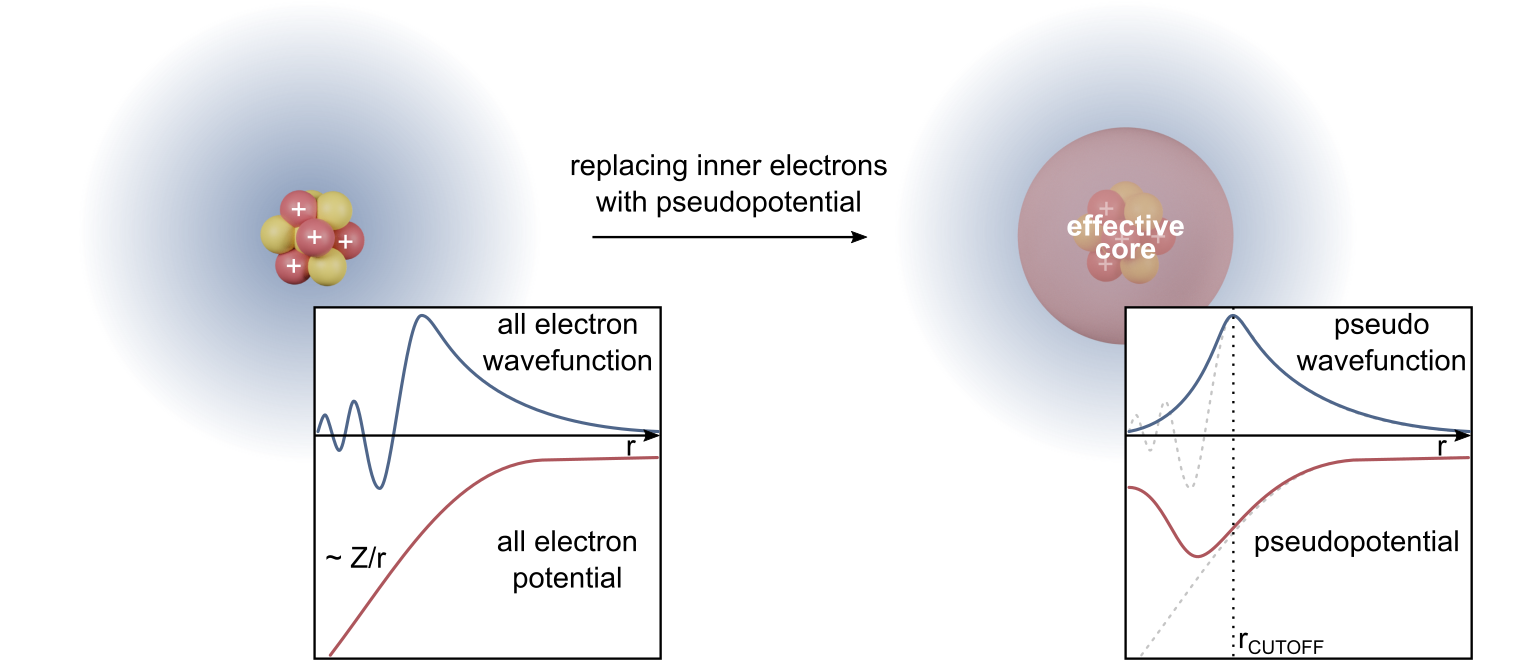
ABINIT
ABINIT is an open-source suite of programs for materials science, distributed under the GNU General Public License. ABINIT implements density functional theory, using a plane wave basis set and pseudopotentials, to compute the electronic density and derived properties of materials ranging from molecules to surfaces to solids. It is developed collaboratively by researchers throughout the world. A web-based easy-to-use graphical version, which includes access to a limited set of ABINIT's full functionality, is available for free use through the nanohub. The latest version 9.10.3 was released on June 24, 2023. Overview ABINIT implements density functional theory by solving the Kohn–Sham equations describing the electrons in a material, expanded in a plane wave basis set and using a self-consistent conjugate gradient method to determine the energy minimum. Computational efficiency is achieved through the use of fast Fourier transforms, and pseudopotentials to describe core electron ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum ESPRESSO
Quantum ESPRESSO (Quantum Open-Source Package for Research in Electronic Structure, Simulation, and Optimization; QE) is a suite for first-principles electronic-structure calculations and materials modeling, distributed for free and as free software under the GNU General Public License. It is based on density functional theory (DFT), plane wave basis sets, and pseudopotentials (both norm-conserving and ultrasoft). The core plane wave DFT functions of QE are provided by the PWscf component (PWscf previously existed as an independent project). PWscf (Plane-Wave Self-Consistent Field) is a set of programs for electronic structure calculations within DFT and density functional perturbation theory, using plane wave basis sets and pseudopotentials. The software is released under the GNU General Public License. The latest stable version QE-7.4.1 was released on 14 March 2025. Quantum ESPRESSO Project Quantum ESPRESSO is an open initiative of the CNR-IOM DEMOCRITOS National Simula ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vienna Ab Initio Simulation Package
The Vienna Ab initio Simulation Package, better known as VASP, is a package written primarily in Fortran for performing ab initio quantum mechanical calculations using either Vanderbilt pseudopotentials, or the projector augmented wave method, and a plane wave basis set. The basic methodology is density functional theory (DFT), but the code also allows use of post-DFT corrections such as hybrid functionals mixing DFT and Hartree–Fock exchange (e.g. HSE, PBE0 or B3LYP), many-body perturbation theory (the GW method) and dynamical electronic correlations within the random phase approximation (RPA) and MP2. Originally, VASP was based on code written by Mike Payne (then at MIT), which was also the basis of CASTEP. It was then brought to the University of Vienna, Austria, in July 1989 by Jürgen Hafner. The main program was written by Jürgen Furthmüller, who joined the group at the Institut für Materialphysik in January 1993, and Georg Kresse. An early version of VASP was ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Density Functional Theory
Density functional theory (DFT) is a computational quantum mechanical modelling method used in physics, chemistry and materials science to investigate the electronic structure (or nuclear structure) (principally the ground state) of many-body systems, in particular atoms, molecules, and the condensed phases. Using this theory, the properties of a many-electron system can be determined by using functionals - that is, functions that accept a function as input and output a single real number. In the case of DFT, these are functionals of the spatially dependent electron density. DFT is among the most popular and versatile methods available in condensed-matter physics, computational physics, and computational chemistry. DFT has been very popular for calculations in solid-state physics since the 1970s. However, DFT was not considered accurate enough for calculations in quantum chemistry until the 1990s, when the approximations used in the theory were greatly refined to better m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fluids
In physics, a fluid is a liquid, gas, or other material that may continuously move and deform (''flow'') under an applied shear stress, or external force. They have zero shear modulus, or, in simpler terms, are substances which cannot resist any shear force applied to them. Although the term ''fluid'' generally includes both the liquid and gas phases, its definition varies among branches of science. Definitions of ''solid'' vary as well, and depending on field, some substances can have both fluid and solid properties. Non-Newtonian fluids like Silly Putty appear to behave similar to a solid when a sudden force is applied. Substances with a very high viscosity such as pitch appear to behave like a solid (see pitch drop experiment) as well. In particle physics, the concept is extended to include fluidic matters other than liquids or gases. A fluid in medicine or biology refers to any liquid constituent of the body (body fluid), whereas "liquid" is not used in this sens ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isotropic
In physics and geometry, isotropy () is uniformity in all orientations. Precise definitions depend on the subject area. Exceptions, or inequalities, are frequently indicated by the prefix ' or ', hence '' anisotropy''. ''Anisotropy'' is also used to describe situations where properties vary systematically, dependent on direction. Isotropic radiation has the same intensity regardless of the direction of measurement, and an isotropic field exerts the same action regardless of how the test particle is oriented. Mathematics Within mathematics, ''isotropy'' has a few different meanings: ; Isotropic manifolds: A manifold is isotropic if the geometry on the manifold is the same regardless of direction. A similar concept is homogeneity. ; Isotropic quadratic form: A quadratic form ''q'' is said to be isotropic if there is a non-zero vector ''v'' such that ; such a ''v'' is an isotropic vector or null vector. In complex geometry, a line through the origin in the direction of an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
P-wave Modulus
There are two kinds of seismic body waves in solids, ''pressure waves'' (P-waves) and ''shear waves.'' In linear elasticity, the P-wave modulus M, also known as the longitudinal modulus, or the constrained modulus, is one of the elastic moduli available to describe isotropic homogeneous materials. It is defined as the ratio of axial stress to axial strain in a uniaxial strain state. This occurs when expansion in the transverse direction is prevented by the inertia of neighboring material, such as in an earthquake, or underwater seismic blast. :\sigma_ = M \epsilon_ where all the other strains \epsilon_ are zero. This is equivalent to stating that :M_ = \rho_ V_\mathrm^2 , where ''V''P is the velocity of a P-wave and ''ρ'' is the density Density (volumetric mass density or specific mass) is the ratio of a substance's mass to its volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' (or ''d'') can al ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
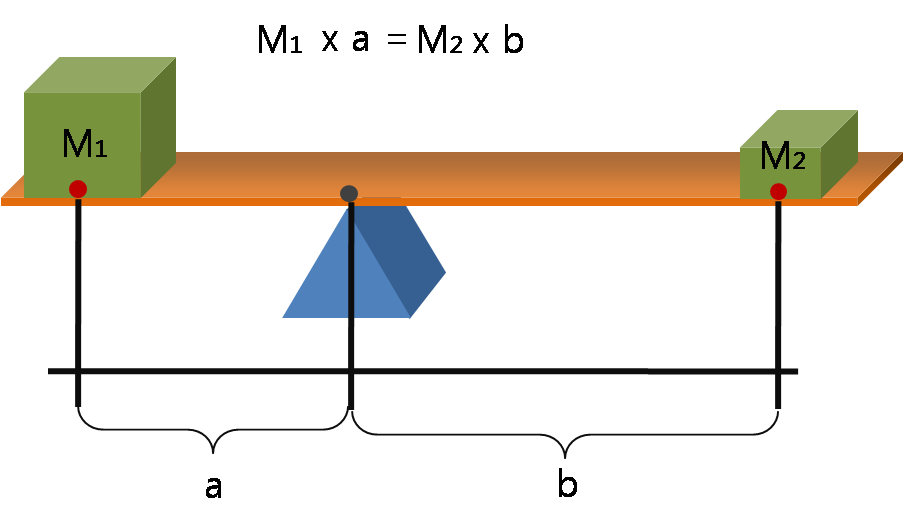
Moment (physics)
A moment is a mathematical expression involving the product of a distance and a physical quantity such as a force or electric charge. Moments are usually defined with respect to a fixed reference point and refer to physical quantities located some distance from the reference point. For example, the moment of force, often called torque, is the product of a force on an object and the distance from the reference point to the object. In principle, any physical quantity can be multiplied by a distance to produce a moment. Commonly used quantities include forces, masses, and electric charge distributions; a list of examples is provided later. Elaboration In its most basic form, a moment is the product of the distance to a point, raised to a power, and a physical quantity (such as force or electrical charge) at that point: : \mu_n = r^n\,Q, where Q is the physical quantity such as a force applied at a point, or a point charge, or a point mass, etc. If the quantity is not concen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |