|
Ein Function
In mathematics, the exponential integral Ei is a special function on the complex plane. It is defined as one particular definite integral of the ratio between an exponential function and its argument of a function, argument. Definitions For real non-zero values of ''x'', the exponential integral Ei(''x'') is defined as : \operatorname(x) = -\int_^\infty \fract\,dt = \int_^x \fract\,dt. The Risch algorithm shows that Ei is not an elementary function. The definition above can be used for positive values of ''x'', but the integral has to be understood in terms of the Cauchy principal value due to the singularity of the integrand at zero. For complex values of the argument, the definition becomes ambiguous due to branch points at 0 and Instead of Ei, the following notation is used, :E_1(z) = \int_z^\infty \frac\, dt,\qquad, (z), 0. Properties Several properties of the exponential integral below, in certain cases, allow one to avoid its explicit evaluation throug ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Integrals Of Exponential Functions
The following is a list of integrals of exponential functions. For a complete list of integral functions, please see the list of integrals. Indefinite integral Indefinite integrals are antiderivative functions. A constant (the constant of integration) may be added to the right hand side of any of these formulas, but has been suppressed here in the interest of brevity. Integrals of polynomials : \int xe^\,dx = e^\left(\frac\right) \text c \neq 0; : \int x^2 e^\,dx = e^\left(\frac-\frac+\frac\right) : \begin \int x^n e^\,dx &= \frac x^n e^ - \frac\int x^ e^ \,dx \\ &= \left( \frac \right)^n \frac \\ &= e^\sum_^n (-1)^i\fracx^ \\ &= e^\sum_^n (-1)^\fracx^i \end : \int\frac\,dx = \ln, x, +\sum_^\infty\frac : \int\frac\,dx = \frac\left(-\frac+c\int\frac\,dx\right) \qquad\textn\neq 1\text Integrals involving only exponential functions : \int f'(x)e^\,dx = e^ : \int e^\,dx = \frac e^ : \int a^\,dx = \frac a^\qquad\texta > 0,\ a \ne 1 Integrals involving the error function ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Catastrophic Cancellation
In numerical analysis, catastrophic cancellation is the phenomenon that subtracting good approximations to two nearby numbers may yield a very bad approximation to the difference of the original numbers. For example, if there are two studs, one L_1 = 254.5\,\text long and the other L_2 = 253.5\,\text long, and they are measured with a ruler that is good only to the centimeter, then the approximations could come out to be \tilde L_1 = 255\,\text and \tilde L_2 = 253\,\text. These may be good approximations, in relative error, to the true lengths: the approximations are in error by less than 2% of the true lengths, , L_1 - \tilde L_1, /, L_1, < 2\%. However, if the ''approximate'' lengths are subtracted, the difference will be , even though the true difference between the lengths is . The difference of the approximations, |
Groundwater
Groundwater is the water present beneath Earth's surface in rock and soil pore spaces and in the fractures of rock formations. About 30 percent of all readily available freshwater in the world is groundwater. A unit of rock or an unconsolidated deposit is called an aquifer when it can yield a usable quantity of water. The depth at which soil pore spaces or fractures and voids in rock become completely saturated with water is called the water table. Groundwater is recharged from the surface; it may discharge from the surface naturally at springs and seeps, and can form oases or wetlands. Groundwater is also often withdrawn for agricultural, municipal, and industrial use by constructing and operating extraction wells. The study of the distribution and movement of groundwater is hydrogeology, also called groundwater hydrology. Typically, groundwater is thought of as water flowing through shallow aquifers, but, in the technical sense, it can also contain soil moisture, perma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
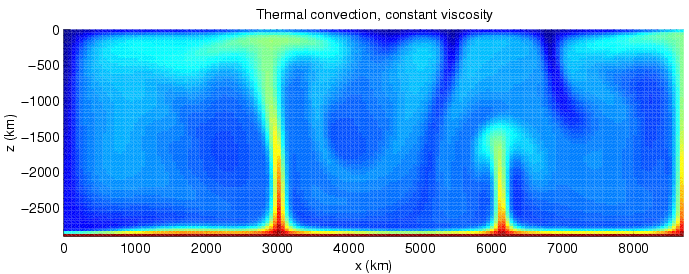
Heat Transfer
Heat transfer is a discipline of thermal engineering that concerns the generation, use, conversion, and exchange of thermal energy (heat) between physical systems. Heat transfer is classified into various mechanisms, such as thermal conduction, Convection (heat transfer), thermal convection, thermal radiation, and transfer of energy by phase changes. Engineers also consider the transfer of mass of differing chemical species (mass transfer in the form of advection), either cold or hot, to achieve heat transfer. While these mechanisms have distinct characteristics, they often occur simultaneously in the same system. Heat conduction, also called diffusion, is the direct microscopic exchanges of kinetic energy of particles (such as molecules) or quasiparticles (such as lattice waves) through the boundary between two systems. When an object is at a different temperature from another body or its surroundings, heat flows so that the body and the surroundings reach the same temperature, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trigonometric Integral
In mathematics, trigonometric integrals are a indexed family, family of integrals involving trigonometric functions. Sine integral The different sine integral definitions are \operatorname(x) = \int_0^x\frac\,dt \operatorname(x) = -\int_x^\infty\frac\,dt~. Note that the integrand is the sinc function, and also the zeroth Bessel function#Spherical Bessel functions: jn.2C yn, spherical Bessel function. Since is an even function, even entire function (holomorphic over the entire complex plane), is entire, odd, and the integral in its definition can be taken along Cauchy's integral theorem, any path connecting the endpoints. By definition, is the antiderivative of whose value is zero at , and is the antiderivative whose value is zero at . Their difference is given by the Dirichlet integral, \operatorname(x) - \operatorname(x) = \int_0^\infty\frac\,dt = \frac \quad \text \quad \operatorname(x) = \frac + \operatorname(x) ~. In signal processing, the oscillations of th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Divisors
In mathematics, a divisor of an integer n, also called a factor of n, is an integer m that may be multiplied by some integer to produce n. In this case, one also says that n is a multiple of m. An integer n is divisible or evenly divisible by another integer m if m is a divisor of n; this implies dividing n by m leaves no remainder. Definition An integer is divisible by a nonzero integer if there exists an integer such that n=km. This is written as :m\mid n. Other ways of saying the same thing are that divides , is a divisor of , is a factor of , and is a multiple of . If does not divide , then the notation is m\not\mid n. Usually, is required to be nonzero, but is allowed to be zero. With this convention, m \mid 0 for every nonzero integer . Some definitions omit the requirement that m be nonzero. General Divisors can be negative as well as positive, although sometimes the term is restricted to positive divisors. For example, there are six divisors of 4; they are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generating Function
In mathematics, a generating function is a way of encoding an infinite sequence of numbers () by treating them as the coefficients of a formal power series. This series is called the generating function of the sequence. Unlike an ordinary series, the ''formal'' power series is not required to converge: in fact, the generating function is not actually regarded as a function, and the "variable" remains an indeterminate. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general linear recurrence problem. One can generalize to formal power series in more than one indeterminate, to encode information about infinite multi-dimensional arrays of numbers. There are various types of generating functions, including ordinary generating functions, exponential generating functions, Lambert series, Bell series, and Dirichlet series; definitions and examples are given below. Every sequence in principle has a generating function of each type (except ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Incomplete Gamma Function
In mathematics, the upper and lower incomplete gamma functions are types of special functions which arise as solutions to various mathematical problems such as certain integrals. Their respective names stem from their integral definitions, which are defined similarly to the gamma function but with different or "incomplete" integral limits. The gamma function is defined as an integral from zero to infinity. This contrasts with the lower incomplete gamma function, which is defined as an integral from zero to a variable upper limit. Similarly, the upper incomplete gamma function is defined as an integral from a variable lower limit to infinity. Definition The upper incomplete gamma function is defined as: \Gamma(s,x) = \int_x^ t^\,e^\, dt , whereas the lower incomplete gamma function is defined as: \gamma(s,x) = \int_0^x t^\,e^\, dt . In both cases is a complex parameter, such that the real part of is positive. Properties By integration by parts we find the recurrence relat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logarithmic Integral Function
In mathematics, the logarithmic integral function or integral logarithm li(''x'') is a special function. It is relevant in problems of physics and has number theoretic significance. In particular, according to the prime number theorem, it is a very good approximation to the prime-counting function, which is defined as the number of prime numbers less than or equal to a given value x. Integral representation The logarithmic integral has an integral representation defined for all positive real numbers ≠ 1 by the definite integral : \operatorname(x) = \int_0^x \frac. Here, denotes the natural logarithm. The function has a singularity at , and the integral for is interpreted as a Cauchy principal value, : \operatorname(x) = \lim_ \left( \int_0^ \frac + \int_^x \frac \right). Offset logarithmic integral The offset logarithmic integral or Eulerian logarithmic integral is defined as : \operatorname(x) = \int_2^x \frac = \operatorname(x) - \operatorname(2). ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Confluent Hypergeometric Functions
In mathematics, a confluent hypergeometric function is a solution of a confluent hypergeometric equation, which is a degenerate form of a hypergeometric differential equation where two of the three regular singularities merge into an irregular singularity. The term ''confluent'' refers to the merging of singular points of families of differential equations; ''confluere'' is Latin for "to flow together". There are several common standard forms of confluent hypergeometric functions: * Kummer's (confluent hypergeometric) function , introduced by , is a solution to Kummer's differential equation. This is also known as the confluent hypergeometric function of the first kind. There is a different and unrelated Kummer's function bearing the same name. * Tricomi's (confluent hypergeometric) function introduced by , sometimes denoted by , is another solution to Kummer's equation. This is also known as the confluent hypergeometric function of the second kind. * Whittaker functions (for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Entire Function
In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic on the whole complex plane. Typical examples of entire functions are polynomials and the exponential function, and any finite sums, products and compositions of these, such as the trigonometric functions sine and cosine and their hyperbolic counterparts sinh and cosh, as well as derivatives and integrals of entire functions such as the error function. If an entire function has a root at , then , taking the limit value at , is an entire function. On the other hand, the natural logarithm, the reciprocal function, and the square root are all not entire functions, nor can they be continued analytically to an entire function. A transcendental entire function is an entire function that is not a polynomial. Properties Every entire function can be represented as a power series f(z) = \sum_^\infty a_n z^n that converges everywhere in the complex plane, hen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |