|
Ehrenfeucht–Mycielski Sequence
The Ehrenfeucht–Mycielski sequence is a recursively defined sequence of binary digits with pseudorandom properties, defined by . Definition The sequence starts with the single bit 0; each successive digit is formed by finding the longest suffix of the sequence that also occurs earlier within the sequence, and complementing the bit following the most recent earlier occurrence of that suffix. (The empty string is a suffix and prefix of every string.) For example, the first few steps of this construction process are: #0: initial bit #01: the suffix "" of "0" occurs earlier, most-recently followed by a 0, so add 1 #010: the suffix "" of "01" occurs earlier, most-recently followed by a 1, so add 0 #0100: the suffix "0" of "010" occurs earlier, most-recently followed by a 1, so add 0 #01001: the suffix "0" of "0100" occurs earlier, most-recently followed by a 0, so add 1 #010011: the suffix "01" of "01001" occurs earlier, most-recently followed by a 0, so add 1 #0100110: the suffix " ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binary Digits
The bit is the most basic unit of information in computing and digital communication. The name is a portmanteau of binary digit. The bit represents a logical state with one of two possible values. These values are most commonly represented as either , but other representations such as ''true''/''false'', ''yes''/''no'', ''on''/''off'', or ''+''/''−'' are also widely used. The relation between these values and the physical states of the underlying storage or device is a matter of convention, and different assignments may be used even within the same device or program. It may be physically implemented with a two-state device. A contiguous group of binary digits is commonly called a ''bit string'', a bit vector, or a single-dimensional (or multi-dimensional) ''bit array''. A group of eight bits is called one ''byte'', but historically the size of the byte is not strictly defined. Frequently, half, full, double and quadruple words consist of a number of bytes which is a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pseudorandom
A pseudorandom sequence of numbers is one that appears to be statistically random, despite having been produced by a completely deterministic and repeatable process. Pseudorandom number generators are often used in computer programming, as traditional sources of randomness available to humans (such as rolling dice) rely on physical processes not readily available to computer programs, although developments in hardware random number generator technology have challenged this. Background The generation of random numbers has many uses, such as for random sampling, Monte Carlo methods, board games, or gambling. In physics, however, most processes, such as gravitational acceleration, are deterministic, meaning that they always produce the same outcome from the same starting point. Some notable exceptions are radioactive decay and quantum measurement, which are both modeled as being truly random processes in the underlying physics. Since these processes are not practical sources of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algorithm
In mathematics and computer science, an algorithm () is a finite sequence of Rigour#Mathematics, mathematically rigorous instructions, typically used to solve a class of specific Computational problem, problems or to perform a computation. Algorithms are used as specifications for performing calculations and data processing. More advanced algorithms can use Conditional (computer programming), conditionals to divert the code execution through various routes (referred to as automated decision-making) and deduce valid inferences (referred to as automated reasoning). In contrast, a Heuristic (computer science), heuristic is an approach to solving problems without well-defined correct or optimal results.David A. Grossman, Ophir Frieder, ''Information Retrieval: Algorithms and Heuristics'', 2nd edition, 2004, For example, although social media recommender systems are commonly called "algorithms", they actually rely on heuristics as there is no truly "correct" recommendation. As an e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Suffix Tree
In computer science, a suffix tree (also called PAT tree or, in an earlier form, position tree) is a compressed trie containing all the suffixes of the given text as their keys and positions in the text as their values. Suffix trees allow particularly fast implementations of many important string operations. The construction of such a tree for the string S takes time and space linear in the length of S. Once constructed, several operations can be performed quickly, such as locating a substring in S, locating a substring if a certain number of mistakes are allowed, and locating matches for a regular expression pattern. Suffix trees also provided one of the first linear-time solutions for the longest common substring problem. These speedups come at a cost: storing a string's suffix tree typically requires significantly more space than storing the string itself. History The concept was first introduced by . Rather than the suffix S ..n/math>, Weiner stored in his trie the ''prefix ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Constant Time
In theoretical computer science, the time complexity is the computational complexity that describes the amount of computer time it takes to run an algorithm. Time complexity is commonly estimated by counting the number of elementary operations performed by the algorithm, supposing that each elementary operation takes a fixed amount of time to perform. Thus, the amount of time taken and the number of elementary operations performed by the algorithm are taken to be related by a constant factor. Since an algorithm's running time may vary among different inputs of the same size, one commonly considers the worst-case time complexity, which is the maximum amount of time required for inputs of a given size. Less common, and usually specified explicitly, is the average-case complexity, which is the average of the time taken on inputs of a given size (this makes sense because there are only a finite number of possible inputs of a given size). In both cases, the time complexity is genera ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Disjunctive Sequence
A disjunctive sequence is an infinite sequence of characters drawn from a finite alphabet, in which every finite string appears as a substring. For instance, the binary Champernowne sequence :0\ 1\ 00\ 01\ 10\ 11\ 000\ 001 \ldots formed by concatenating all binary strings in shortlex order, clearly contains all the binary strings and so is disjunctive. (The spaces above are not significant and are present solely to make clear the boundaries between strings). The complexity function of a disjunctive sequence ''S'' over an alphabet of size ''k'' is ''p''''S''(''n'') = ''k''''n''.Bugeaud (2012) p.91 Any normal sequence (a sequence in which each string of equal length appears with equal frequency) is disjunctive, but the converse is not true. For example, letting 0''n'' denote the string of length ''n'' consisting of all 0s, consider the sequence :0\ 0^1\ 1\ 0^2\ 00\ 0^4\ 01\ 0^8\ 10\ 0^\ 11\ 0^\ 000\ 0^\ldots obtained by splicing exponentially long strings of 0s into the s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ackermann Function
In computability theory, the Ackermann function, named after Wilhelm Ackermann, is one of the simplest and earliest-discovered examples of a total function, total computable function that is not Primitive recursive function, primitive recursive. All primitive recursive functions are total and computable, but the Ackermann function illustrates that not all total computable functions are primitive recursive. After Ackermann's publication of his function (which had three non-negative integer arguments), many authors modified it to suit various purposes, so that today "the Ackermann function" may refer to any of numerous variants of the original function. One common version is the two-argument Ackermann–Péter function developed by Rózsa Péter and Raphael Robinson. This function is defined from the recurrence relation \operatorname(m+1, n+1) = \operatorname(m, \operatorname(m+1, n)) with appropriate Base case (recursion), base cases. Its value grows very rapidly; for example, \o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
De Bruijn Sequence
In combinatorics, combinatorial mathematics, a de Bruijn sequence of order ''n'' on a size-''k'' alphabet (computer science), alphabet ''A'' is a cyclic sequence in which every possible length-''n'' String (computer science)#Formal theory, string on ''A'' occurs exactly once as a substring (i.e., as a ''contiguous'' subsequence). Such a sequence is denoted by and has length , which is also the number of distinct strings of length ''n'' on ''A''. Each of these distinct strings, when taken as a substring of , must start at a different position, because substrings starting at the same position are not distinct. Therefore, must have ''at least'' symbols. And since has ''exactly'' symbols, de Bruijn sequences are optimally short with respect to the property of containing every string of length ''n'' at least once. The number of distinct de Bruijn sequences is :\dfrac. For a binary alphabet this is 2^, leading to the following sequence for positive n: 1, 1, 2, 16, 2048, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convergence Rate
In mathematical analysis, particularly numerical analysis, the rate of convergence and order of convergence of a sequence that converges to a Limit of a sequence, limit are any of several characterizations of how quickly that sequence approaches its limit. These are broadly divided into rates and orders of convergence that describe how quickly a sequence further approaches its limit once it is already close to it, called Asymptotic analysis, asymptotic rates and orders of convergence, and those that describe how quickly sequences approach their limits from starting points that are not necessarily close to their limits, called non-asymptotic rates and orders of convergence. Asymptotic behavior is particularly useful for deciding when to stop a sequence of numerical computations, for instance once a target precision has been reached with an iterative root-finding algorithm, but pre-asymptotic behavior is often crucial for determining whether to begin a sequence of computations at ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Random Sequence
The concept of a random sequence is essential in probability theory and statistics. The concept generally relies on the notion of a sequence of random variables and many statistical discussions begin with the words "let ''X''1,...,''Xn'' be independent random variables...". Yet as D. H. Lehmer stated in 1951: "A random sequence is a vague notion... in which each term is unpredictable to the uninitiated and whose digits pass a certain number of tests traditional with statisticians". Axiomatic probability theory ''deliberately'' avoids a definition of a random sequence. Traditional probability theory does not state if a specific sequence is random, but generally proceeds to discuss the properties of random variables and stochastic sequences assuming some definition of randomness. The Bourbaki school considered the statement "let us consider a random sequence" an abuse of language. Early history Émile Borel was one of the first mathematicians to formally address randomness in 190 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
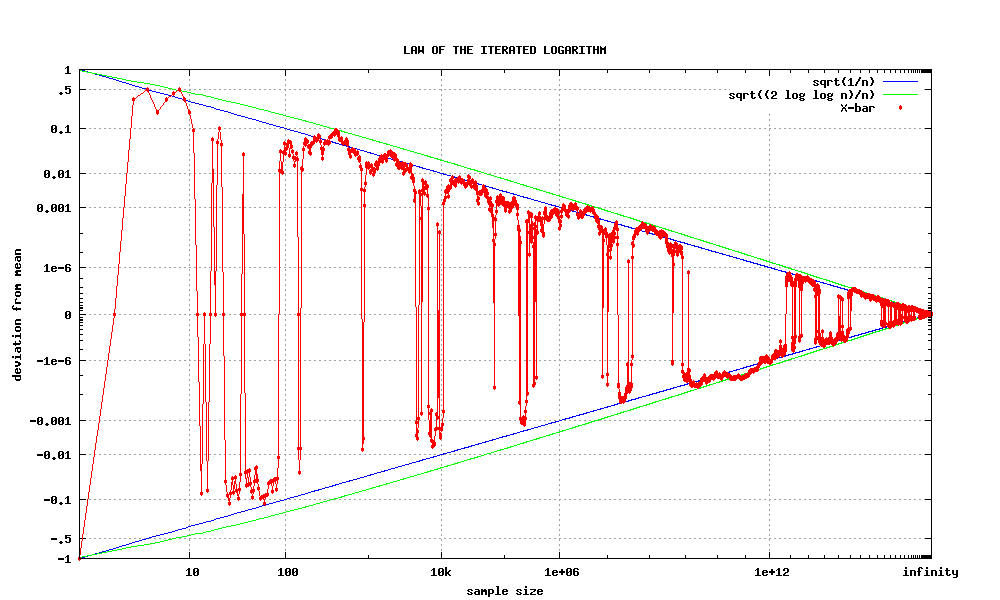
Law Of The Iterated Logarithm
In probability theory, the law of the iterated logarithm describes the magnitude of the fluctuations of a random walk. The original statement of the law of the iterated logarithm is due to Aleksandr Khinchin, A. Ya. Khinchin (1924). Another statement was given by Andrey Kolmogorov, A. N. Kolmogorov in 1929.Andrey Kolmogorov, A. Kolmogoroff"Über das Gesetz des iterierten Logarithmus" ''Mathematische Annalen'', 101: 126–135, 1929. Statement Let be independent, identically distributed random variables with zero means and unit variances. Let ''S''''n'' = ''Y''1 + ... + ''Y''''n''. Then : \limsup_ \frac = 1 \quad \text, where "log" is the natural logarithm, "lim sup" denotes the limit superior, and "a.s." stands for "almost surely". Another statement given by Andrey Kolmogorov, A. N. Kolmogorov in 1929 is as follows. Let \ be independent random variables with zero means and finite variances. Let S_n = Y_1 + \dots + Y_n and B_n = \operatorname(Y_1) + \dots + \operator ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Normal Number
In mathematics, a real number is said to be simply normal in an integer base b if its infinite sequence of digits is distributed uniformly in the sense that each of the b digit values has the same natural density 1/b. A number is said to be normal in base b if, for every positive integer n, all possible strings n digits long have density b−''n''. Intuitively, a number being simply normal means that no digit occurs more frequently than any other. If a number is normal, no finite combination of digits of a given length occurs more frequently than any other combination of the same length. A normal number can be thought of as an infinite sequence of coin flips ( binary) or rolls of a die ( base 6). Even though there ''will'' be sequences such as 10, 100, or more consecutive tails (binary) or fives (base 6) or even 10, 100, or more repetitions of a sequence such as tail-head (two consecutive coin flips) or 6-1 (two consecutive rolls of a die), there will also be equally ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |