|
Eckart Conditions
The Eckart conditions, named after Carl Eckart, simplify the nuclear motion (rovibrational) Hamiltonian that arises in the second step of the Born–Oppenheimer approximation. They make it possible to approximately separate rotation from vibration. Although the rotational and vibrational motions of the nuclei in a molecule cannot be fully separated, the Eckart conditions minimize the coupling close to a reference (usually equilibrium) configuration. The Eckart conditions are explained by Louck and Galbraith and in Section 10.2 of the textbook by Bunker and Jensen, where a numerical example is given. Definition of Eckart conditions The Eckart conditions can only be formulated for a semi-rigid molecule, which is a molecule with a potential energy surface ''V''(R1, R2,..R''N'') that has a well-defined minimum for R''A''0 (A=1,\ldots, N). These equilibrium coordinates of the nuclei—with masses ''M''''A''—are expressed with respect to a fixed orthonormal principal axes frame an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Carl Eckart
Carl Henry Eckart (May 4, 1902 – October 23, 1973) was an American physicist, physical oceanographer, geophysicist, and administrator. He co-developed the Wigner–Eckart theorem and is also known for the Eckart conditions in quantum mechanics, and the Eckart–Young theorem in linear algebra. Early life Eckart was born in St. Louis, Missouri. He began college in 1919 at Washington University in St. Louis where he received his B.S. and M.S. degrees with a major in engineering. However, due to Arthur Holly Compton, a physics faculty member and later Chancellor, Eckart was influenced to continue his education in physics at Princeton, where he went in 1923 on an Edison Lamp Works Research Fellowship. Eckart was awarded his Ph.D. in 1925.Eckart Biography – The National Academies Press [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Physical Review
''Physical Review'' is a peer-reviewed scientific journal established in 1893 by Edward Nichols. It publishes original research as well as scientific and literature reviews on all aspects of physics. It is published by the American Physical Society (APS). The journal is in its third series, and is split in several sub-journals each covering a particular field of physics. It has a sister journal, ''Physical Review Letters'', which publishes shorter articles of broader interest. History ''Physical Review'' commenced publication in July 1893, organized by Cornell University professor Edward Nichols and helped by the new president of Cornell, J. Gould Schurman. The journal was managed and edited at Cornell in upstate New York from 1893 to 1913 by Nichols, Ernest Merritt, and Frederick Bedell. The 33 volumes published during this time constitute ''Physical Review Series I''. The American Physical Society (APS), founded in 1899, took over its publication in 1913 and star ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Born–Oppenheimer Approximation
In quantum chemistry and molecular physics, the Born–Oppenheimer (BO) approximation is the best-known mathematical approximation in molecular dynamics. Specifically, it is the assumption that the wave functions of atomic nuclei and electrons in a molecule can be treated separately, based on the fact that the nuclei are much heavier than the electrons. Due to the larger relative mass of a nucleus compared to an electron, the coordinates of the nuclei in a system are approximated as fixed, while the coordinates of the electrons are dynamic. The approach is named after Max Born and J. Robert Oppenheimer who proposed it in 1927, in the early period of quantum mechanics. The approximation is widely used in quantum chemistry to speed up the computation of molecular wavefunctions and other properties for large molecules. There are cases where the assumption of separable motion no longer holds, which make the approximation lose validity (it is said to "break down"), but even then ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Semi-rigid Molecule
In chemistry and molecular physics, fluxional (or non-rigid) molecules are molecules that undergo dynamics such that some or all of their atoms interchange between symmetry-equivalent positions. Because virtually all molecules are fluxional in some respects, e.g. bond rotations in most organic compounds, the term fluxional depends on the context and the method used to assess the dynamics. Often, a molecule is considered fluxional if its spectroscopic signature exhibits line-broadening (beyond that dictated by the Heisenberg uncertainty principle) due to chemical exchange. In some cases, where the rates are slow, fluxionality is not detected spectroscopically, but by isotopic labeling and other methods. Spectroscopic studies Many organometallic compounds exhibit fluxionality. Fluxionality is however pervasive. NMR spectroscopy Temperature dependent changes in the NMR spectra result from dynamics associated with the fluxional molecules when those dynamics proceed at rates co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
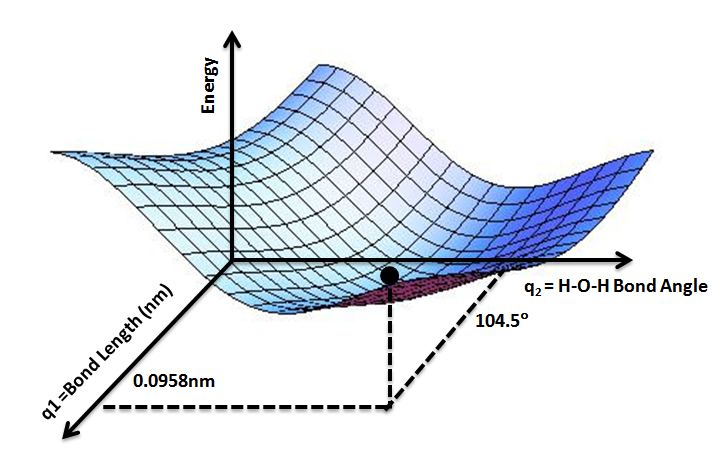
Potential Energy Surface
A potential energy surface (PES) describes the energy of a system, especially a collection of atoms, in terms of certain parameters, normally the positions of the atoms. The surface might define the energy as a function of one or more coordinates; if there is only one coordinate, the surface is called a ''potential energy curve'' or energy profile. An example is the Morse/Long-range potential. It is helpful to use the analogy of a landscape: for a system with two degrees of freedom (e.g. two bond lengths), the value of the energy (analogy: the height of the land) is a function of two bond lengths (analogy: the coordinates of the position on the ground). The PES concept finds application in fields such as chemistry and physics, especially in the theoretical sub-branches of these subjects. It can be used to theoretically explore properties of structures composed of atoms, for example, finding the minimum energy shape of a molecule or computing the rates of a chemical reacti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Moment Of Inertia Tensor
The moment of inertia, otherwise known as the mass moment of inertia, angular mass, second moment of mass, or most accurately, rotational inertia, of a rigid body is a quantity that determines the torque needed for a desired angular acceleration about a rotational axis, akin to how mass determines the force needed for a desired acceleration. It depends on the body's mass distribution and the axis chosen, with larger moments requiring more torque to change the body's rate of rotation. It is an extensive (additive) property: for a point mass the moment of inertia is simply the mass times the square of the perpendicular distance to the axis of rotation. The moment of inertia of a rigid composite system is the sum of the moments of inertia of its component subsystems (all taken about the same axis). Its simplest definition is the second moment of mass with respect to distance from an axis. For bodies constrained to rotate in a plane, only their moment of inertia about an axi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vector Product
In mathematics, the cross product or vector product (occasionally directed area product, to emphasize its geometric significance) is a binary operation on two vectors in a three-dimensional oriented Euclidean vector space (named here E), and is denoted by the symbol \times. Given two linearly independent vectors and , the cross product, (read "a cross b"), is a vector that is perpendicular to both and , and thus normal to the plane containing them. It has many applications in mathematics, physics, engineering, and computer programming. It should not be confused with the dot product (projection product). If two vectors have the same direction or have the exact opposite direction from each other (that is, they are ''not'' linearly independent), or if either one has zero length, then their cross product is zero. More generally, the magnitude of the product equals the area of a parallelogram with the vectors for sides; in particular, the magnitude of the product of two perpendicu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rigid Rotor
In rotordynamics, the rigid rotor is a mechanical model of rotating systems. An arbitrary rigid rotor is a 3-dimensional rigid object, such as a top. To orient such an object in space requires three angles, known as Euler angles. A special rigid rotor is the ''linear rotor'' requiring only two angles to describe, for example of a diatomic molecule. More general molecules are 3-dimensional, such as water (asymmetric rotor), ammonia (symmetric rotor), or methane (spherical rotor). Linear rotor The linear rigid rotor model consists of two point masses located at fixed distances from their center of mass. The fixed distance between the two masses and the values of the masses are the only characteristics of the rigid model. However, for many actual diatomics this model is too restrictive since distances are usually not completely fixed. Corrections on the rigid model can be made to compensate for small variations in the distance. Even in such a case the rigid rotor model is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
GF Method
The GF method, sometimes referred to as FG method, is a classical mechanical method introduced by Edgar Bright Wilson to obtain certain ''internal coordinates'' for a vibrating semi-rigid molecule, the so-called ''normal coordinates'' ''Q''k. Normal coordinates decouple the classical vibrational motions of the molecule and thus give an easy route to obtaining vibrational amplitudes of the atoms as a function of time. In Wilson's GF method it is assumed that the molecular kinetic energy consists only of harmonic vibrations of the atoms, ''i.e.,'' overall rotational and translational energy is ignored. Normal coordinates appear also in a quantum mechanical description of the vibrational motions of the molecule and the Coriolis coupling between rotations and vibrations. It follows from application of the Eckart conditions that the matrix G−1 gives the kinetic energy in terms of arbitrary linear internal coordinates, while F represents the (harmonic) potential energy in terms of th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Infrared Spectroscopy
Infrared spectroscopy (IR spectroscopy or vibrational spectroscopy) is the measurement of the interaction of infrared radiation with matter by absorption, emission, or reflection. It is used to study and identify chemical substances or functional groups in solid, liquid, or gaseous forms. It can be used to characterize new materials or identify and verify known and unknown samples. The method or technique of infrared spectroscopy is conducted with an instrument called an infrared spectrometer (or spectrophotometer) which produces an infrared spectrum. An IR spectrum can be visualized in a graph of infrared light absorbance (or transmittance) on the vertical axis vs. frequency, wavenumber or wavelength on the horizontal axis. Typical units of wavenumber used in IR spectra are reciprocal centimeters, with the symbol cm−1. Units of IR wavelength are commonly given in micrometers (formerly called "microns"), symbol μm, which are related to the wavenumber in a reciprocal way. A ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generalized Eigenvalue Problem
In linear algebra, eigendecomposition is the factorization of a matrix into a canonical form, whereby the matrix is represented in terms of its eigenvalues and eigenvectors. Only diagonalizable matrices can be factorized in this way. When the matrix being factorized is a normal or real symmetric matrix, the decomposition is called "spectral decomposition", derived from the spectral theorem. Fundamental theory of matrix eigenvectors and eigenvalues A (nonzero) vector of dimension is an eigenvector of a square matrix if it satisfies a linear equation of the form :\mathbf \mathbf = \lambda \mathbf for some scalar . Then is called the eigenvalue corresponding to . Geometrically speaking, the eigenvectors of are the vectors that merely elongates or shrinks, and the amount that they elongate/shrink by is the eigenvalue. The above equation is called the eigenvalue equation or the eigenvalue problem. This yields an equation for the eigenvalues : p\left(\lambda\right) = \det\l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hessian Matrix
In mathematics, the Hessian matrix or Hessian is a square matrix of second-order partial derivatives of a scalar-valued function, or scalar field. It describes the local curvature of a function of many variables. The Hessian matrix was developed in the 19th century by the German mathematician Ludwig Otto Hesse and later named after him. Hesse originally used the term "functional determinants". Definitions and properties Suppose f : \R^n \to \R is a function taking as input a vector \mathbf \in \R^n and outputting a scalar f(\mathbf) \in \R. If all second-order partial derivatives of f exist, then the Hessian matrix \mathbf of f is a square n \times n matrix, usually defined and arranged as follows: \mathbf H_f= \begin \dfrac & \dfrac & \cdots & \dfrac \\ .2ex \dfrac & \dfrac & \cdots & \dfrac \\ .2ex \vdots & \vdots & \ddots & \vdots \\ .2ex \dfrac & \dfrac & \cdots & \dfrac \end, or, by stating an equation for the coefficients using indices i and j, (\mathbf H_f)_ = \fra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |