|
Dirichlet L-function
In mathematics, a Dirichlet ''L''-series is a function of the form :L(s,\chi) = \sum_^\infty \frac. where \chi is a Dirichlet character and ''s'' a complex variable with real part greater than 1. It is a special case of a Dirichlet series. By analytic continuation, it can be extended to a meromorphic function on the whole complex plane, and is then called a Dirichlet ''L''-function and also denoted ''L''(''s'', ''χ''). These functions are named after Peter Gustav Lejeune Dirichlet who introduced them in to prove the theorem on primes in arithmetic progressions that also bears his name. In the course of the proof, Dirichlet shows that is non-zero at ''s'' = 1. Moreover, if ''χ'' is principal, then the corresponding Dirichlet ''L''-function has a simple pole at ''s'' = 1. Otherwise, the ''L''-function is entire. Euler product Since a Dirichlet character ''χ'' is completely multiplicative, its ''L''-function can also be written as an Euler product in the half-plane of absol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
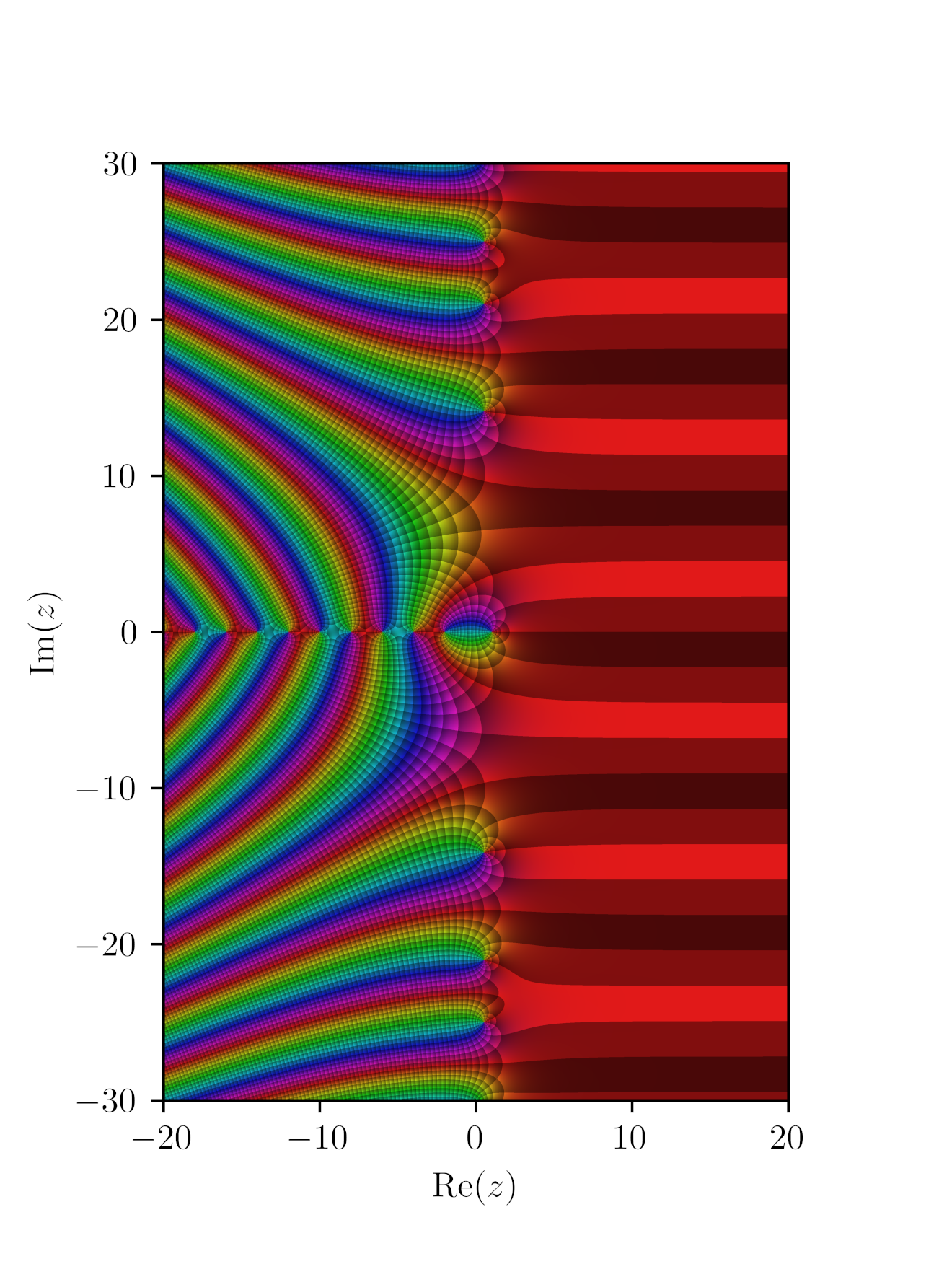
Riemann Zeta Function
The Riemann zeta function or Euler–Riemann zeta function, denoted by the Greek letter (zeta), is a mathematical function of a complex variable defined as \zeta(s) = \sum_^\infty \frac = \frac + \frac + \frac + \cdots for \operatorname(s) > 1 and its analytic continuation elsewhere. The Riemann zeta function plays a pivotal role in analytic number theory, and has applications in physics, probability theory, and applied statistics. Leonhard Euler first introduced and studied the function over the reals in the first half of the eighteenth century. Bernhard Riemann's 1859 article "On the Number of Primes Less Than a Given Magnitude" extended the Euler definition to a complex variable, proved its meromorphic continuation and functional equation, and established a relation between its zeros and the distribution of prime numbers. This paper also contained the Riemann hypothesis, a conjecture about the distribution of complex zeros of the Riemann zeta function that is consid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
L-function
In mathematics, an ''L''-function is a meromorphic function on the complex plane, associated to one out of several categories of mathematical objects. An ''L''-series is a Dirichlet series, usually convergent on a half-plane, that may give rise to an ''L''-function via analytic continuation. The Riemann zeta function is an example of an ''L''-function, and one important conjecture involving ''L''-functions is the Riemann hypothesis and its generalization. The theory of ''L''-functions has become a very substantial, and still largely conjectural, part of contemporary analytic number theory. In it, broad generalisations of the Riemann zeta function and the ''L''-series for a Dirichlet character are constructed, and their general properties, in most cases still out of reach of proof, are set out in a systematic way. Because of the Euler product formula there is a deep connection between ''L''-functions and the theory of prime numbers. The mathematical field that studies L-func ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generalized Riemann Hypothesis
The Riemann hypothesis is one of the most important conjectures in mathematics. It is a statement about the zeros of the Riemann zeta function. Various geometrical and arithmetical objects can be described by so-called global ''L''-functions, which are formally similar to the Riemann zeta-function. One can then ask the same question about the zeros of these ''L''-functions, yielding various generalizations of the Riemann hypothesis. Many mathematicians believe these generalizations of the Riemann hypothesis to be true. The only cases of these conjectures which have been proven occur in the algebraic function field case (not the number field case). Global ''L''-functions can be associated to elliptic curves, number fields (in which case they are called Dedekind zeta-functions), Maass forms, and Dirichlet characters (in which case they are called Dirichlet L-functions). When the Riemann hypothesis is formulated for Dedekind zeta-functions, it is known as the extended Riemann hypothes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hurwitz Zeta Function
In mathematics, the Hurwitz zeta function is one of the many zeta functions. It is formally defined for complex variables with and by :\zeta(s,a) = \sum_^\infty \frac. This series is absolutely convergent for the given values of and and can be extended to a meromorphic function defined for all . The Riemann zeta function is . The Hurwitz zeta function is named after Adolf Hurwitz, who introduced it in 1882. Integral representation The Hurwitz zeta function has an integral representation :\zeta(s,a) = \frac \int_0^\infty \frac dx for \operatorname(s)>1 and \operatorname(a)>0. (This integral can be viewed as a Mellin transform.) The formula can be obtained, roughly, by writing :\zeta(s,a)\Gamma(s) = \sum_^\infty \frac \int_0^\infty x^s e^ \frac = \sum_^\infty \int_0^\infty y^s e^ \frac and then interchanging the sum and integral. The integral representation above can be converted to a contour integral representation :\zeta(s,a) = -\Gamma(1-s)\frac \int_C \frac dz where ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
American Mathematical Society
The American Mathematical Society (AMS) is an association of professional mathematicians dedicated to the interests of mathematical research and scholarship, and serves the national and international community through its publications, meetings, advocacy and other programs. The society is one of the four parts of the Joint Policy Board for Mathematics and a member of the Conference Board of the Mathematical Sciences. History The AMS was founded in 1888 as the New York Mathematical Society, the brainchild of Thomas Fiske, who was impressed by the London Mathematical Society on a visit to England. John Howard Van Amringe was the first president and Fiske became secretary. The society soon decided to publish a journal, but ran into some resistance, due to concerns about competing with the American Journal of Mathematics. The result was the ''Bulletin of the American Mathematical Society'', with Fiske as editor-in-chief. The de facto journal, as intended, was influential in in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Siegel Zero
Siegel (also Segal or Segel), is a German and Ashkenazi Jewish surname. it can be traced to 11th century Bavaria and was used by people who made wax seals for or sealed official documents (each such male being described as a ''Siegelbeamter''). Alternate spellings include Sigel, Sigl, Siegl, and others. "Siegel" is also the modern German word for seal. The name ultimately derives from the Latin ''sigillum,'' meaning "seal" as in the Seal of the City of New York: ''Sigillum Civitatis Novi Eboraci''. The Germanicized derivative of the name was given to professional seal makers and engravers. Some researchers have attributed the surname to Sigel, referring to Sól (Sun), the goddess of the sun in Germanic mythology (Siȝel or sigel in Old English / Anglo-Saxon), but that is highly speculative. Variants, and false cognates Other variants may routinely include Siegelman, Siegle, Sigl, and Sigel. Presumably, some bearers of these names are lineal descendants of ethnic Jews who chan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generalized Riemann Hypothesis
The Riemann hypothesis is one of the most important conjectures in mathematics. It is a statement about the zeros of the Riemann zeta function. Various geometrical and arithmetical objects can be described by so-called global ''L''-functions, which are formally similar to the Riemann zeta-function. One can then ask the same question about the zeros of these ''L''-functions, yielding various generalizations of the Riemann hypothesis. Many mathematicians believe these generalizations of the Riemann hypothesis to be true. The only cases of these conjectures which have been proven occur in the algebraic function field case (not the number field case). Global ''L''-functions can be associated to elliptic curves, number fields (in which case they are called Dedekind zeta-functions), Maass forms, and Dirichlet characters (in which case they are called Dirichlet L-functions). When the Riemann hypothesis is formulated for Dedekind zeta-functions, it is known as the extended Riemann hypothes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integer
An integer is the number zero (), a positive natural number (, , , etc.) or a negative integer with a minus sign (−1, −2, −3, etc.). The negative numbers are the additive inverses of the corresponding positive numbers. In the language of mathematics, the set of integers is often denoted by the boldface or blackboard bold \mathbb. The set of natural numbers \mathbb is a subset of \mathbb, which in turn is a subset of the set of all rational numbers \mathbb, itself a subset of the real numbers \mathbb. Like the natural numbers, \mathbb is countably infinite. An integer may be regarded as a real number that can be written without a fractional component. For example, 21, 4, 0, and −2048 are integers, while 9.75, , and are not. The integers form the smallest group and the smallest ring containing the natural numbers. In algebraic number theory, the integers are sometimes qualified as rational integers to distinguish them from the more general algebraic integers ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zero Of A Function
In mathematics, a zero (also sometimes called a root) of a real-, complex-, or generally vector-valued function f, is a member x of the domain of f such that f(x) ''vanishes'' at x; that is, the function f attains the value of 0 at x, or equivalently, x is the solution to the equation f(x) = 0. A "zero" of a function is thus an input value that produces an output of 0. A root of a polynomial is a zero of the corresponding polynomial function. The fundamental theorem of algebra shows that any non-zero polynomial has a number of roots at most equal to its degree, and that the number of roots and the degree are equal when one considers the complex roots (or more generally, the roots in an algebraically closed extension) counted with their multiplicities. For example, the polynomial f of degree two, defined by f(x)=x^2-5x+6 has the two roots (or zeros) that are 2 and 3. f(2)=2^2-5\times 2+6= 0\textf(3)=3^2-5\times 3+6=0. If the function maps real numbers to real numbers, then it ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Functional Equation (L-function)
In mathematics, the L-functions of number theory are expected to have several characteristic properties, one of which is that they satisfy certain functional equations. There is an elaborate theory of what these equations should be, much of which is still conjectural. Introduction A prototypical example, the Riemann zeta function has a functional equation relating its value at the complex number ''s'' with its value at 1 − ''s''. In every case this relates to some value ζ(''s'') that is only defined by analytic continuation from the infinite series definition. That is, writingas is conventionalσ for the real part of ''s'', the functional equation relates the cases :σ > 1 and σ < 0, and also changes a case with :0 < σ < 1 in the ''critical strip'' to another such case, reflected in the line σ = ½. Therefore, use of the functional equation is basic, in order to study the zeta-function in the whole |