|
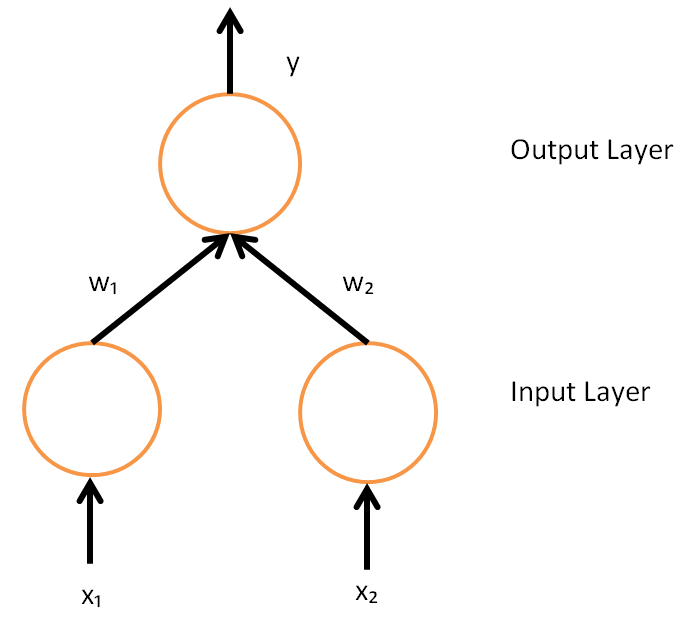
Delta Rule
In machine learning, the delta rule is a gradient descent learning rule for updating the weights of the inputs to artificial neurons in a single-layer neural network. It is a special case of the more general backpropagation algorithm. For a neuron j with activation function g(x) , the delta rule for neuron j 's i th weight w_ is given by :\Delta w_=\alpha(t_j-y_j) g'(h_j) x_i , where It holds that h_j=\sum x_i w_ and y_j=g(h_j) . The delta rule is commonly stated in simplified form for a neuron with a linear activation function as :\Delta w_=\alpha(t_j-y_j) x_i While the delta rule is similar to the perceptron's update rule, the derivation is different. The perceptron uses the Heaviside step function as the activation function g(h), and that means that g'(h) does not exist at zero, and is equal to zero elsewhere, which makes the direct application of the delta rule impossible. Derivation of the delta rule The delta rule is derived by attempting to minimize th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Machine Learning
Machine learning (ML) is a field of inquiry devoted to understanding and building methods that 'learn', that is, methods that leverage data to improve performance on some set of tasks. It is seen as a part of artificial intelligence. Machine learning algorithms build a model based on sample data, known as training data, in order to make predictions or decisions without being explicitly programmed to do so. Machine learning algorithms are used in a wide variety of applications, such as in medicine, email filtering, speech recognition, agriculture, and computer vision, where it is difficult or unfeasible to develop conventional algorithms to perform the needed tasks.Hu, J.; Niu, H.; Carrasco, J.; Lennox, B.; Arvin, F.,Voronoi-Based Multi-Robot Autonomous Exploration in Unknown Environments via Deep Reinforcement Learning IEEE Transactions on Vehicular Technology, 2020. A subset of machine learning is closely related to computational statistics, which focuses on making pred ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gradient Descent
In mathematics, gradient descent (also often called steepest descent) is a first-order iterative optimization algorithm for finding a local minimum of a differentiable function. The idea is to take repeated steps in the opposite direction of the gradient (or approximate gradient) of the function at the current point, because this is the direction of steepest descent. Conversely, stepping in the direction of the gradient will lead to a local maximum of that function; the procedure is then known as gradient ascent. Gradient descent is generally attributed to Augustin-Louis Cauchy, who first suggested it in 1847. Jacques Hadamard independently proposed a similar method in 1907. Its convergence properties for non-linear optimization problems were first studied by Haskell Curry in 1944, with the method becoming increasingly well-studied and used in the following decades. Description Gradient descent is based on the observation that if the multi-variable function F(\mathbf) is de ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Artificial Neurons
An artificial neuron is a mathematical function conceived as a model of biological neurons, a neural network. Artificial neurons are elementary units in an artificial neural network. The artificial neuron receives one or more inputs (representing excitatory postsynaptic potentials and inhibitory postsynaptic potentials at neural dendrites) and sums them to produce an output (or , representing a neuron's action potential which is transmitted along its axon). Usually each input is separately weighted, and the sum is passed through a non-linear function known as an activation function or transfer function. The transfer functions usually have a sigmoid shape, but they may also take the form of other non-linear functions, piecewise linear functions, or step functions. They are also often monotonically increasing, continuous, differentiable and bounded. Non-monotonic, unbounded and oscillating activation functions with multiple zeros that outperform sigmoidal and ReLU like activation f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Feedforward Neural Network
A feedforward neural network (FNN) is an artificial neural network wherein connections between the nodes do ''not'' form a cycle. As such, it is different from its descendant: recurrent neural networks. The feedforward neural network was the first and simplest type of artificial neural network devised. In this network, the information moves in only one direction—forward—from the input nodes, through the hidden nodes (if any) and to the output nodes. There are no cycles or loops in the network. Single-layer perceptron The simplest kind of neural network is a ''single-layer perceptron'' network, which consists of a single layer of output nodes; the inputs are fed directly to the outputs via a series of weights. The sum of the products of the weights and the inputs is calculated in each node, and if the value is above some threshold (typically 0) the neuron fires and takes the activated value (typically 1); otherwise it takes the deactivated value (typically -1). N ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Backpropagation
In machine learning, backpropagation (backprop, BP) is a widely used algorithm for training feedforward artificial neural networks. Generalizations of backpropagation exist for other artificial neural networks (ANNs), and for functions generally. These classes of algorithms are all referred to generically as "backpropagation". In fitting a neural network, backpropagation computes the gradient of the loss function with respect to the weights of the network for a single input–output example, and does so efficiently, unlike a naive direct computation of the gradient with respect to each weight individually. This efficiency makes it feasible to use gradient methods for training multilayer networks, updating weights to minimize loss; gradient descent, or variants such as stochastic gradient descent, are commonly used. The backpropagation algorithm works by computing the gradient of the loss function with respect to each weight by the chain rule, computing the gradient one lay ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Activation Function
In artificial neural networks, the activation function of a node defines the output of that node given an input or set of inputs. A standard integrated circuit can be seen as a digital network of activation functions that can be "ON" (1) or "OFF" (0), depending on input. This is similar to the linear perceptron in neural networks. However, only ''nonlinear'' activation functions allow such networks to compute nontrivial problems using only a small number of nodes, and such activation functions are called nonlinearities. Classification of activation functions The most common activation functions can be divided in three categories: ridge functions, radial functions and fold functions. An activation function f is saturating if \lim_ , \nabla f(v), = 0. It is nonsaturating if it is not saturating. Non-saturating activation functions, such as ReLU, may be better than saturating activation functions, as they don't suffer from vanishing gradient. Ridge activation functions ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Learning Rate
In machine learning and statistics, the learning rate is a tuning parameter in an optimization algorithm that determines the step size at each iteration while moving toward a minimum of a loss function. Since it influences to what extent newly acquired information overrides old information, it metaphorically represents the speed at which a machine learning model "learns". In the adaptive control literature, the learning rate is commonly referred to as gain. In setting a learning rate, there is a trade-off between the rate of convergence and overshooting. While the descent direction is usually determined from the gradient of the loss function, the learning rate determines how big a step is taken in that direction. A too high learning rate will make the learning jump over minima but a too low learning rate will either take too long to converge or get stuck in an undesirable local minimum. In order to achieve faster convergence, prevent oscillations and getting stuck in undesi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Derivative
In mathematics, the derivative of a function of a real variable measures the sensitivity to change of the function value (output value) with respect to a change in its argument (input value). Derivatives are a fundamental tool of calculus. For example, the derivative of the position of a moving object with respect to time is the object's velocity: this measures how quickly the position of the object changes when time advances. The derivative of a function of a single variable at a chosen input value, when it exists, is the slope of the tangent line to the graph of the function at that point. The tangent line is the best linear approximation of the function near that input value. For this reason, the derivative is often described as the "instantaneous rate of change", the ratio of the instantaneous change in the dependent variable to that of the independent variable. Derivatives can be generalized to functions of several real variables. In this generalization, the de ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perceptron
In machine learning, the perceptron (or McCulloch-Pitts neuron) is an algorithm for supervised learning of binary classifiers. A binary classifier is a function which can decide whether or not an input, represented by a vector of numbers, belongs to some specific class. It is a type of linear classifier, i.e. a classification algorithm that makes its predictions based on a linear predictor function combining a set of weights with the feature vector. History The perceptron was invented in 1943 by McCulloch and Pitts. The first implementation was a machine built in 1958 at the Cornell Aeronautical Laboratory by Frank Rosenblatt, funded by the United States Office of Naval Research. The perceptron was intended to be a machine, rather than a program, and while its first implementation was in software for the IBM 704, it was subsequently implemented in custom-built hardware as the "Mark 1 perceptron". This machine was designed for image recognition: it had an array of 400 photoc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heaviside Step Function
The Heaviside step function, or the unit step function, usually denoted by or (but sometimes , or ), is a step function, named after Oliver Heaviside (1850–1925), the value of which is zero for negative arguments and one for positive arguments. It is an example of the general class of step functions, all of which can be represented as linear combinations of translations of this one. The function was originally developed in operational calculus for the solution of differential equations, where it represents a signal that switches on at a specified time and stays switched on indefinitely. Oliver Heaviside, who developed the operational calculus as a tool in the analysis of telegraphic communications, represented the function as . The Heaviside function may be defined as: * a piecewise function: H(x) := \begin 1, & x > 0 \\ 0, & x \le 0 \end * using the Iverson bracket notation: H(x) := 0.html" ;"title=">0">>0/math> * an indicator function: H(x) := \mathbf_=\mathbf 1_(x ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant (as opposed to the total derivative, in which all variables are allowed to vary). Partial derivatives are used in vector calculus and differential geometry. The partial derivative of a function f(x, y, \dots) with respect to the variable x is variously denoted by It can be thought of as the rate of change of the function in the x-direction. Sometimes, for z=f(x, y, \ldots), the partial derivative of z with respect to x is denoted as \tfrac. Since a partial derivative generally has the same arguments as the original function, its functional dependence is sometimes explicitly signified by the notation, such as in: :f'_x(x, y, \ldots), \frac (x, y, \ldots). The symbol used to denote partial derivatives is ∂. One of the first known uses of this symbol in mathematics is by Marquis de Condorcet from 1770, who used it f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chain Rule
In calculus, the chain rule is a formula that expresses the derivative of the composition of two differentiable functions and in terms of the derivatives of and . More precisely, if h=f\circ g is the function such that h(x)=f(g(x)) for every , then the chain rule is, in Lagrange's notation, :h'(x) = f'(g(x)) g'(x). or, equivalently, :h'=(f\circ g)'=(f'\circ g)\cdot g'. The chain rule may also be expressed in Leibniz's notation. If a variable depends on the variable , which itself depends on the variable (that is, and are dependent variables), then depends on as well, via the intermediate variable . In this case, the chain rule is expressed as :\frac = \frac \cdot \frac, and : \left.\frac\_ = \left.\frac\_ \cdot \left. \frac\_ , for indicating at which points the derivatives have to be evaluated. In integration, the counterpart to the chain rule is the substitution rule. Intuitive explanation Intuitively, the chain rule states that knowing the instantaneous rate of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |