|
Datum Reference
A datum reference or just datum (plural: datumsThe plural of this sense of the word '' datum'' is ''datums'' by convention, in contrast with the other senses of the word in which ''data'' usually serves as both the plural form and the mass noun counterpart.) ) is some important part of an object—such as a point, line, plane, hole, set of holes, or pair of surfaces—that serves as a reference in defining the geometry of the object and (often) in measuring aspects of the actual geometry to assess how closely they match with the nominal value, which may be an ideal, standard, average, or desired value. For example, on a car's wheel, the lug nut holes define a bolt circle that is a datum from which the location of the rim can be defined and measured. This matters because the hub and rim need to be concentric to within close limits (or else the wheel will not roll smoothly). The concept of datums is used in many fields, including carpentry, metalworking, needlework, geometric ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Word Sense
In linguistics, a word sense is one of the meanings of a word. For example, a dictionary may have over 50 different senses of the word "play", each of these having a different meaning based on the context of the word's usage in a sentence, as follows: In each sentence different collocates of "play" signal its different meanings. People and computers, as they read words, must use a process called word-sense disambiguationR. Navigli''Word Sense Disambiguation: A Survey', ACM Computing Surveys, 41(2), 2009, pp. 1-69. to reconstruct the likely intended meaning of a word. This process uses context to narrow the possible senses down to the probable ones. The context includes such things as the ideas conveyed by adjacent words and nearby phrases, the known or probable purpose and register of the conversation or document, and the orientation (time and place) implied or expressed. The disambiguation is thus context-sensitive. Advanced semantic analysis has resulted in a s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Aviation
Aviation includes the activities surrounding mechanical flight and the aircraft industry. ''Aircraft'' includes fixed-wing and rotary-wing types, morphable wings, wing-less lifting bodies, as well as lighter-than-air craft such as hot air balloons and airships. Aviation began in the 18th century with the development of the hot air balloon, an apparatus capable of atmospheric displacement through buoyancy. Some of the most significant advancements in aviation technology came with the controlled gliding flying of Otto Lilienthal in 1896; then a large step in significance came with the construction of the first powered airplane by the Wright brothers in the early 1900s. Since that time, aviation has been technologically revolutionized by the introduction of the jet which permitted a major form of transport throughout the world. Etymology The word ''aviation'' was coined by the French writer and former naval officer Gabriel La Landelle in 1863. He derived the term from th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coordinate System
In geometry, a coordinate system is a system that uses one or more numbers, or coordinates, to uniquely determine the position of the points or other geometric elements on a manifold such as Euclidean space. The order of the coordinates is significant, and they are sometimes identified by their position in an ordered tuple and sometimes by a letter, as in "the ''x''-coordinate". The coordinates are taken to be real numbers in elementary mathematics, but may be complex numbers or elements of a more abstract system such as a commutative ring. The use of a coordinate system allows problems in geometry to be translated into problems about numbers and ''vice versa''; this is the basis of analytic geometry. Common coordinate systems Number line The simplest example of a coordinate system is the identification of points on a line with real numbers using the '' number line''. In this system, an arbitrary point ''O'' (the ''origin'') is chosen on a given line. The coordinate of a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Degrees Of Freedom (mechanics)
In physics, the degrees of freedom (DOF) of a mechanical system is the number of independent parameters that define its configuration or state. It is important in the analysis of systems of bodies in mechanical engineering, structural engineering, aerospace engineering, robotics, and other fields. The position of a single railcar (engine) moving along a track has one degree of freedom because the position of the car is defined by the distance along the track. A train of rigid cars connected by hinges to an engine still has only one degree of freedom because the positions of the cars behind the engine are constrained by the shape of the track. An automobile with highly stiff suspension can be considered to be a rigid body traveling on a plane (a flat, two-dimensional space). This body has three independent degrees of freedom consisting of two components of translation and one angle of rotation. Skidding or drifting is a good example of an automobile's three independent degrees ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tolerance Analysis
Tolerance analysis is the general term for activities related to the study of accumulated variation in mechanical parts and assemblies. Its methods may be used on other types of systems subject to accumulated variation, such as mechanical and electrical systems. Engineers analyze tolerances for the purpose of evaluating geometric dimensioning and tolerancing (GD&T). Methods include 2D tolerance stacks, 3D Monte Carlo simulations, and datum conversions. Tolerance stackups or tolerance stacks are used to describe the problem-solving process in mechanical engineering of calculating the effects of the accumulated variation that is allowed by specified dimensions and tolerances. Typically these dimensions and tolerances are specified on an engineering drawing. Arithmetic tolerance stackups use the worst-case maximum or minimum values of dimensions and tolerances to calculate the maximum and minimum distance (clearance or interference) between two features or parts. Statistical toler ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
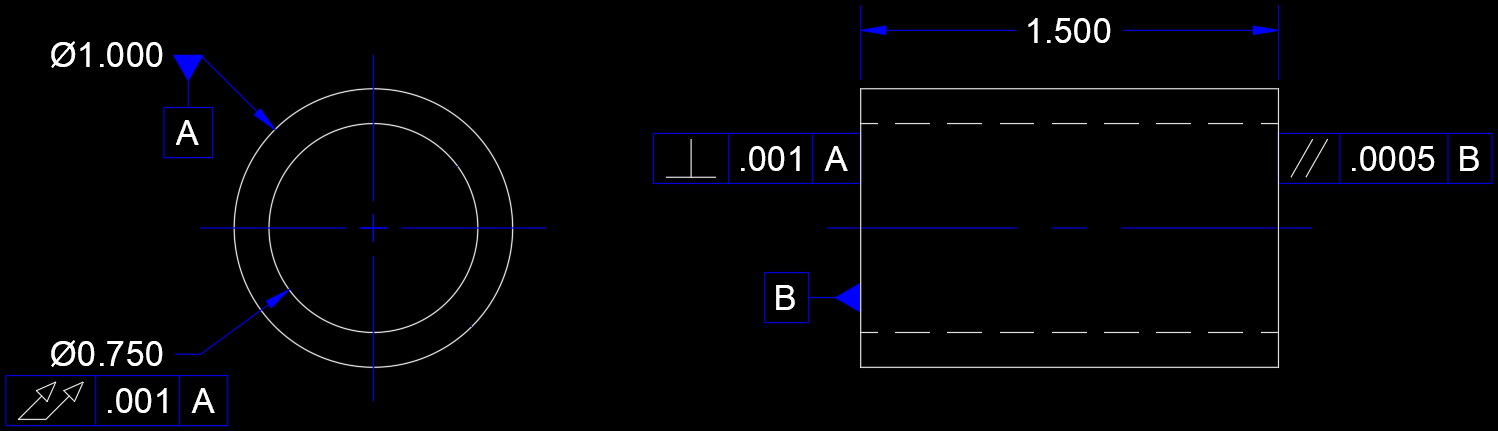
Feature Control Frame
Geometric Dimensioning and Tolerancing (GD&T) is a system for defining and communicating engineering tolerances and relationships. It uses a symbolic language on engineering drawings and computer-generated three-dimensional solid models that explicitly describe nominal geometry and its allowable variation. It tells the manufacturing staff and machines what degree of accuracy and precision is needed on each controlled feature of the part. GD&T is used to define the nominal (theoretically perfect) geometry of parts and assemblies, to define the allowable variation in form and possible size of individual features, and to define the allowable variation between features. *Dimensioning specifications define the nominal, as-modeled or as-intended geometry. One example is a basic dimension. *Tolerancing specifications define the allowable variation for the form and possibly the size of individual features, and the allowable variation in orientation and location between features. Two exam ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Three-dimensional Space
Three-dimensional space (also: 3D space, 3-space or, rarely, tri-dimensional space) is a geometric setting in which three values (called ''parameters'') are required to determine the position of an element (i.e., point). This is the informal meaning of the term dimension. In mathematics, a tuple of numbers can be understood as the Cartesian coordinates of a location in a -dimensional Euclidean space. The set of these -tuples is commonly denoted \R^n, and can be identified to the -dimensional Euclidean space. When , this space is called three-dimensional Euclidean space (or simply Euclidean space when the context is clear). It serves as a model of the physical universe (when relativity theory is not considered), in which all known matter exists. While this space remains the most compelling and useful way to model the world as it is experienced, it is only one example of a large variety of spaces in three dimensions called 3-manifolds. In this classical example, when the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Engineering Drawing
An engineering drawing is a type of technical drawing that is used to convey information about an object. A common use is to specify the geometry necessary for the construction of a component and is called a detail drawing. Usually, a number of drawings are necessary to completely specify even a simple component. The drawings are linked together by a master drawing or assembly drawing which gives the ''drawing numbers'' of the subsequent detailed components, quantities required, construction materials and possibly 3D images that can be used to locate individual items. Although mostly consisting of pictographic representations, abbreviations and symbols are used for brevity and additional textual explanations may also be provided to convey the necessary information. The process of producing engineering drawings is often referred to as technical drawing or drafting (draughting). Drawings typically contain multiple views of a component, although additional ''scratch views'' ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Engineering
Engineering is the use of scientific principles to design and build machines, structures, and other items, including bridges, tunnels, roads, vehicles, and buildings. The discipline of engineering encompasses a broad range of more specialized fields of engineering, each with a more specific emphasis on particular areas of applied mathematics, applied science, and types of application. See glossary of engineering. The term ''engineering'' is derived from the Latin ''ingenium'', meaning "cleverness" and ''ingeniare'', meaning "to contrive, devise". Definition The American Engineers' Council for Professional Development (ECPD, the predecessor of ABET) has defined "engineering" as: The creative application of scientific principles to design or develop structures, machines, apparatus, or manufacturing processes, or works utilizing them singly or in combination; or to construct or operate the same with full cognizance of their design; or to forecast their behavior under speci ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Measurement
Measurement is the quantification of attributes of an object or event, which can be used to compare with other objects or events. In other words, measurement is a process of determining how large or small a physical quantity is as compared to a basic reference quantity of the same kind. The scope and application of measurement are dependent on the context and discipline. In natural sciences and engineering, measurements do not apply to nominal properties of objects or events, which is consistent with the guidelines of the ''International vocabulary of metrology'' published by the International Bureau of Weights and Measures. However, in other fields such as statistics as well as the social and behavioural sciences, measurements can have multiple levels, which would include nominal, ordinal, interval and ratio scales. Measurement is a cornerstone of trade, science, technology and quantitative research in many disciplines. Historically, many measurement systems existed f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Annotation 2019-10-08 224945
An annotation is extra information associated with a particular point in a document or other piece of information. It can be a note that includes a comment or explanation. Annotations are sometimes presented in the margin of book pages. For annotations of different digital media, see web annotation and text annotation. Literature and education Textual scholarship Textual scholarship is a discipline that often uses the technique of annotation to describe or add additional historical context to texts and physical documents to make it easier to understand. Student uses Students often highlight passages in books in order to refer back to key phrases easily, or add marginalia to aid studying. Annotated bibliographies add commentary on the relevance or quality of each source, in addition to the usual bibliographic information that merely identifies the source. Mathematical expression annotation Mathematical expressions (symbols and formulae) can be annotated with their natura ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perpendicular
In elementary geometry, two geometric objects are perpendicular if they intersect at a right angle (90 degrees or π/2 radians). The condition of perpendicularity may be represented graphically using the ''perpendicular symbol'', ⟂. It can be defined between two lines (or two line segments), between a line and a plane, and between two planes. Perpendicularity is one particular instance of the more general mathematical concept of '' orthogonality''; perpendicularity is the orthogonality of classical geometric objects. Thus, in advanced mathematics, the word "perpendicular" is sometimes used to describe much more complicated geometric orthogonality conditions, such as that between a surface and its '' normal vector''. Definitions A line is said to be perpendicular to another line if the two lines intersect at a right angle. Explicitly, a first line is perpendicular to a second line if (1) the two lines meet; and (2) at the point of intersection the straight angle on one sid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |