|
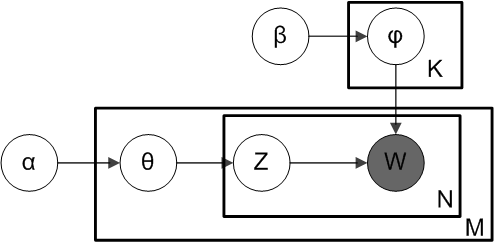
Dynamic Topic Model
Within statistics, ''Dynamic topic models are generative models that can be used to analyze the evolution of (unobserved) topics of a collection of documents over time. This family of models was proposed by David Blei and John Lafferty and is an extension to Latent Dirichlet Allocation (LDA) that can handle sequential documents. In LDA, both the order the words appear in a document and the order the documents appear in the corpus are oblivious to the model. Whereas words are still assumed to be De Finetti's theorem, exchangeable, in a dynamic topic model the order of the documents plays a fundamental role. More precisely, the documents are grouped by time slice (e.g.: years) and it is assumed that the documents of each group come from a set of topics that evolved from the set of the previous slice. Topics Similarly to Latent Dirichlet allocation, LDA and pLSA, in a dynamic topic model, each document is viewed as a mixture of unobserved topics. Furthermore, each topic defines a multi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German: '' Statistik'', "description of a state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of surveys and experiments.Dodge, Y. (2006) ''The Oxford Dictionary of Statistical Terms'', Oxford University Press. When census data cannot be collected, statisticians collect data by developing specific experiment designs and survey samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample to the population as a whole. An ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generative Model
In statistical classification, two main approaches are called the generative approach and the discriminative approach. These compute classifiers by different approaches, differing in the degree of statistical modelling. Terminology is inconsistent, but three major types can be distinguished, following : # A generative model is a statistical model of the joint probability distribution P(X, Y) on given observable variable ''X'' and target variable ''Y'';: "Generative classifiers learn a model of the joint probability, p(x, y), of the inputs ''x'' and the label ''y'', and make their predictions by using Bayes rules to calculate p(y\mid x), and then picking the most likely label ''y''. # A discriminative model is a model of the conditional probability P(Y\mid X = x) of the target ''Y'', given an observation ''x''; and # Classifiers computed without using a probability model are also referred to loosely as "discriminative". The distinction between these last two classes is not ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
David Blei
David Meir Blei is a professor in the Statistics and Computer Science departments at Columbia University. Prior to fall 2014 he was an associate professor in the Department of Computer Science at Princeton University. His work is primarily in machine learning. Research His research interests include topic models and he was one of the original developers of latent Dirichlet allocation, along with Andrew Ng and Michael I. Jordan. As of June 18, 2020, his publications have been cited 109,821 times, giving him an h-index of 97. Honors and awards Blei received the ACM Infosys Foundation Award in 2013. (This award is given to a computer scientist under the age of 45. It has since been renamed the ACM Prize in Computing.) He was named Fellow of ACM ACM or A.C.M. may refer to: Aviation * AGM-129 ACM, 1990–2012 USAF cruise missile * Air chief marshal * Air combat manoeuvring or dogfighting * Air cycle machine * Arica Airport (Colombia) (IATA: ACM), in Arica, Amazonas, Colombia Compu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Latent Dirichlet Allocation
In natural language processing, Latent Dirichlet Allocation (LDA) is a generative statistical model that explains a set of observations through unobserved groups, and each group explains why some parts of the data are similar. The LDA is an example of a topic model. In this, observations (e.g., words) are collected into documents, and each word's presence is attributable to one of the document's topics. Each document will contain a small number of topics. History In the context of population genetics, LDA was proposed by J. K. Pritchard, M. Stephens and P. Donnelly in 2000. LDA was applied in machine learning by David Blei, Andrew Ng and Michael I. Jordan in 2003. Overview Evolutionary biology and bio-medicine In evolutionary biology and bio-medicine, the model is used to detect the presence of structured genetic variation in a group of individuals. The model assumes that alleles carried by individuals under study have origin in various extant or past populations. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
De Finetti's Theorem
In probability theory, de Finetti's theorem states that exchangeable observations are conditionally independent relative to some latent variable. An epistemic probability distribution could then be assigned to this variable. It is named in honor of Bruno de Finetti. For the special case of an exchangeable sequence of Bernoulli random variables it states that such a sequence is a " mixture" of sequences of independent and identically distributed (i.i.d.) Bernoulli random variables. A sequence of random variables is called exchangeable if the joint distribution of the sequence is unchanged by any permutation of the indices. While the variables of the exchangeable sequence are not ''themselves'' independent, only exchangeable, there is an ''underlying'' family of i.i.d. random variables. That is, there are underlying, generally unobservable, quantities that are i.i.d. – exchangeable sequences are mixtures of i.i.d. sequences. Background A Bayesian statistician often seeks t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Latent Dirichlet Allocation
In natural language processing, Latent Dirichlet Allocation (LDA) is a generative statistical model that explains a set of observations through unobserved groups, and each group explains why some parts of the data are similar. The LDA is an example of a topic model. In this, observations (e.g., words) are collected into documents, and each word's presence is attributable to one of the document's topics. Each document will contain a small number of topics. History In the context of population genetics, LDA was proposed by J. K. Pritchard, M. Stephens and P. Donnelly in 2000. LDA was applied in machine learning by David Blei, Andrew Ng and Michael I. Jordan in 2003. Overview Evolutionary biology and bio-medicine In evolutionary biology and bio-medicine, the model is used to detect the presence of structured genetic variation in a group of individuals. The model assumes that alleles carried by individuals under study have origin in various extant or past populations. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
PLSA
Probabilistic latent semantic analysis (PLSA), also known as probabilistic latent semantic indexing (PLSI, especially in information retrieval circles) is a statistical technique for the analysis of two-mode and co-occurrence data. In effect, one can derive a low-dimensional representation of the observed variables in terms of their affinity to certain hidden variables, just as in latent semantic analysis, from which PLSA evolved. Compared to standard latent semantic analysis which stems from linear algebra and downsizes the occurrence tables (usually via a singular value decomposition), probabilistic latent semantic analysis is based on a mixture decomposition derived from a latent class model. Model Considering observations in the form of co-occurrences (w,d) of words and documents, PLSA models the probability of each co-occurrence as a mixture of conditionally independent multinomial distributions: : P(w,d) = \sum_c P(c) P(d, c) P(w, c) = P(d) \sum_c P(c, d) P(w, c) with c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multinomial Distribution
In probability theory, the multinomial distribution is a generalization of the binomial distribution. For example, it models the probability of counts for each side of a ''k''-sided dice rolled ''n'' times. For ''n'' independent trials each of which leads to a success for exactly one of ''k'' categories, with each category having a given fixed success probability, the multinomial distribution gives the probability of any particular combination of numbers of successes for the various categories. When ''k'' is 2 and ''n'' is 1, the multinomial distribution is the Bernoulli distribution. When ''k'' is 2 and ''n'' is bigger than 1, it is the binomial distribution. When ''k'' is bigger than 2 and ''n'' is 1, it is the categorical distribution. The term "multinoulli" is sometimes used for the categorical distribution to emphasize this four-way relationship (so ''n'' determines the prefix, and ''k'' the suffix). The Bernoulli distribution models the outcome of a single Bernoulli tri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exponential Family
In probability and statistics, an exponential family is a parametric set of probability distributions of a certain form, specified below. This special form is chosen for mathematical convenience, including the enabling of the user to calculate expectations, covariances using differentiation based on some useful algebraic properties, as well as for generality, as exponential families are in a sense very natural sets of distributions to consider. The term exponential class is sometimes used in place of "exponential family", or the older term Koopman–Darmois family. The terms "distribution" and "family" are often used loosely: specifically, ''an'' exponential family is a ''set'' of distributions, where the specific distribution varies with the parameter; however, a parametric ''family'' of distributions is often referred to as "''a'' distribution" (like "the normal distribution", meaning "the family of normal distributions"), and the set of all exponential families is sometimes l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gibbs Sampling
In statistics, Gibbs sampling or a Gibbs sampler is a Markov chain Monte Carlo (MCMC) algorithm for obtaining a sequence of observations which are approximated from a specified multivariate probability distribution, when direct sampling is difficult. This sequence can be used to approximate the joint distribution (e.g., to generate a histogram of the distribution); to approximate the marginal distribution of one of the variables, or some subset of the variables (for example, the unknown parameters or latent variables); or to compute an integral (such as the expected value of one of the variables). Typically, some of the variables correspond to observations whose values are known, and hence do not need to be sampled. Gibbs sampling is commonly used as a means of statistical inference, especially Bayesian inference. It is a randomized algorithm (i.e. an algorithm that makes use of random numbers), and is an alternative to deterministic algorithms for statistical inference su ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Variational Methods
The calculus of variations (or Variational Calculus) is a field of mathematical analysis that uses variations, which are small changes in functions and functionals, to find maxima and minima of functionals: mappings from a set of functions to the real numbers. Functionals are often expressed as definite integrals involving functions and their derivatives. Functions that maximize or minimize functionals may be found using the Euler–Lagrange equation of the calculus of variations. A simple example of such a problem is to find the curve of shortest length connecting two points. If there are no constraints, the solution is a straight line between the points. However, if the curve is constrained to lie on a surface in space, then the solution is less obvious, and possibly many solutions may exist. Such solutions are known as ''geodesics''. A related problem is posed by Fermat's principle: light follows the path of shortest optical length connecting two points, which depends upo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Latent Variable Models
Latency or latent may refer to: Science and technology * Latent heat, energy released or absorbed, by a body or a thermodynamic system, during a constant-temperature process * Latent variable, a variable that is not directly observed but inferred in statistics Biology and medicine * Latency period or latent period, the time between development of a disease or exposure to a pathogen, chemical, or radiation and when symptoms first become apparent (e.g. latent tumor) or when the disease becomes infectious (e.g. infectious disease) * Latent homosexuality, a term proposed by Sigmund Freud * Sleep onset latency, the time it takes a person to fall asleep * Virus latency, the ability of a virus to remain dormant Engineering * Latency (engineering), a measure of the time delay experienced by a system ** Latency (audio), the delay necessitated by the conversion between analog and digital representations of sound data ** CAS latency, computer memory latency ** Network latency Network del ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |