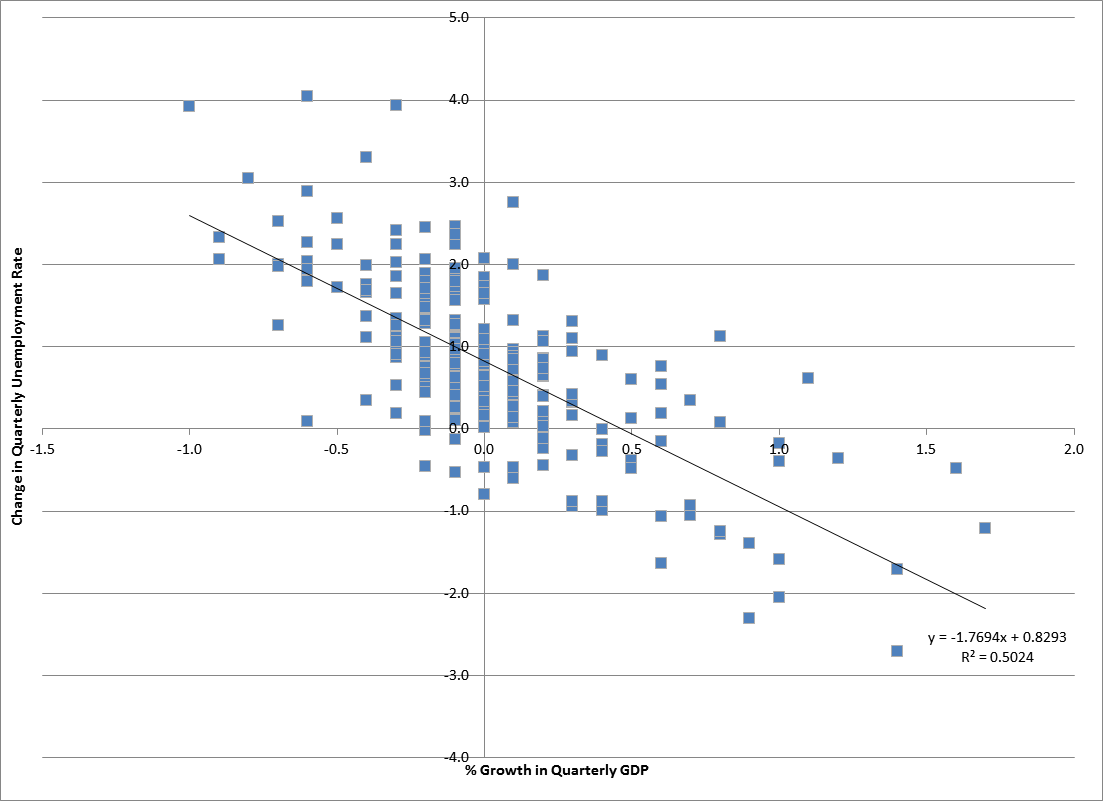
|
Dynamic Factor
In econometrics, a dynamic factor (also known as a diffusion index) is a series which measures the co-movement of many time series. It is used in certain macroeconomic models. A diffusion index is intended to indicate * the changes of the fraction of economic data time series which increase or decrease over the selected time interval, * an increase or decrease in future economic activity, * provide some correlation to the business sentiment of companies. Formally : X_=\Lambda_F_+e_, where F_=(f^_,\dots,f^_) is the vector of lagged factors of the variables in the T \times N matrix X_ (T is the number of observations and N is the number of variables), \Lambda_ are the factor loadings, and e_ is the factor error. History Diffusion indexes were originally designed to help identify business cycle turning points. Example A diffusion index of monthly employment levels across industries measures the degree to which a growth in employment levels in a population is made up of grow ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Econometrics
Econometrics is the application of Statistics, statistical methods to economic data in order to give Empirical evidence, empirical content to economic relationships.M. Hashem Pesaran (1987). "Econometrics," ''The New Palgrave: A Dictionary of Economics'', v. 2, p. 8 [pp. 8–22]. Reprinted in J. Eatwell ''et al.'', eds. (1990). ''Econometrics: The New Palgrave''p. 1[pp. 1–34].Abstract (The New Palgrave Dictionary of Economics, 2008 revision by J. Geweke, J. Horowitz, and H. P. Pesaran). More precisely, it is "the quantitative analysis of actual economic Phenomenon, phenomena based on the concurrent development of theory and observation, related by appropriate methods of inference". An introductory economics textbook describes econometrics as allowing economists "to sift through mountains of data to extract simple relationships". Jan Tinbergen is one of the two founding fathers of econometrics. The other, Ragnar Frisch, also coined the term in the sense in which it is used toda ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Time Series
In mathematics, a time series is a series of data points indexed (or listed or graphed) in time order. Most commonly, a time series is a sequence taken at successive equally spaced points in time. Thus it is a sequence of discrete-time data. Examples of time series are heights of ocean tides, counts of sunspots, and the daily closing value of the Dow Jones Industrial Average. A time series is very frequently plotted via a run chart (which is a temporal line chart). Time series are used in statistics, signal processing, pattern recognition, econometrics, mathematical finance, weather forecasting, earthquake prediction, electroencephalography, control engineering, astronomy, communications engineering, and largely in any domain of applied science and engineering which involves temporal measurements. Time series ''analysis'' comprises methods for analyzing time series data in order to extract meaningful statistics and other characteristics of the data. Time series ''forecasting' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Macroeconomic Model
A macroeconomic model is an analytical tool designed to describe the operation of the problems of economy of a country or a region. These models are usually designed to examine the comparative statics and dynamics of aggregate quantities such as the total amount of goods and services produced, total income earned, the level of employment of productive resources, and the level of prices. Macroeconomic models may be logical, mathematical, and/or computational; the different types of macroeconomic models serve different purposes and have different advantages and disadvantages. Macroeconomic models may be used to clarify and illustrate basic theoretical principles; they may be used to test, compare, and quantify different macroeconomic theories; they may be used to produce "what if" scenarios (usually to predict the effects of changes in monetary, fiscal, or other macroeconomic policies); and they may be used to generate economic forecasts. Thus, macroeconomic models are widely use ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Monthly Labor Review
The ''Monthly Labor Review'' (''MLR'') is published by the U.S. Bureau of Labor Statistics (BLS). Issues often focus on a particular topic. Most articles are by BLS staff. Annually since 1969, the Lawrence R. Klein Award has been awarded to authors of articles appearing in the ''Monthly Labor Review'', generally one to BLS authors and one to non-BLS authors. History In 1915, under commissioner Royal Meeker Royal Meeker (February 23, 1873 – August 16, 1953) was a progressive American economist, born at Quaker Lake, Susquehanna County, Pennsylvania. He graduated from Iowa State College in 1898, then studied with E.R.A. Seligman at Columbia (Ph.D ..., BLS began publishing the ''Monthly Review'', with a circulation of 8,000. The name became ''Monthly Labor Review'' in 1918, and circulation rose to 20,000 in June 1920.Joseph Goldberg and William Moye. 1985. First hundred years of the Bureau of Labor Statistics'. BLS Bulletin 2235. p 110. The journal has published its arti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vector Space
In mathematics and physics, a vector space (also called a linear space) is a set whose elements, often called ''vectors'', may be added together and multiplied ("scaled") by numbers called '' scalars''. Scalars are often real numbers, but can be complex numbers or, more generally, elements of any field. The operations of vector addition and scalar multiplication must satisfy certain requirements, called ''vector axioms''. The terms real vector space and complex vector space are often used to specify the nature of the scalars: real coordinate space or complex coordinate space. Vector spaces generalize Euclidean vectors, which allow modeling of physical quantities, such as forces and velocity, that have not only a magnitude, but also a direction. The concept of vector spaces is fundamental for linear algebra, together with the concept of matrix, which allows computing in vector spaces. This provides a concise and synthetic way for manipulating and studying systems of linear eq ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Variable (mathematics)
In mathematics, a variable (from Latin '' variabilis'', "changeable") is a symbol that represents a mathematical object. A variable may represent a number, a vector, a matrix, a function, the argument of a function, a set, or an element of a set. Algebraic computations with variables as if they were explicit numbers solve a range of problems in a single computation. For example, the quadratic formula solves any quadratic equation by substituting the numeric values of the coefficients of that equation for the variables that represent them in the quadratic formula. In mathematical logic, a ''variable'' is either a symbol representing an unspecified term of the theory (a meta-variable), or a basic object of the theory that is manipulated without referring to its possible intuitive interpretation. History In ancient works such as Euclid's ''Elements'', single letters refer to geometric points and shapes. In the 7th century, Brahmagupta used different colours to represent the u ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matrix (mathematics)
In mathematics, a matrix (plural matrices) is a rectangular array or table of numbers, symbols, or expressions, arranged in rows and columns, which is used to represent a mathematical object or a property of such an object. For example, \begin1 & 9 & -13 \\20 & 5 & -6 \end is a matrix with two rows and three columns. This is often referred to as a "two by three matrix", a "-matrix", or a matrix of dimension . Without further specifications, matrices represent linear maps, and allow explicit computations in linear algebra. Therefore, the study of matrices is a large part of linear algebra, and most properties and operations of abstract linear algebra can be expressed in terms of matrices. For example, matrix multiplication represents composition of linear maps. Not all matrices are related to linear algebra. This is, in particular, the case in graph theory, of incidence matrices, and adjacency matrices. ''This article focuses on matrices related to linear algebra, and, unle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Error
An error (from the Latin ''error'', meaning "wandering") is an action which is inaccurate or incorrect. In some usages, an error is synonymous with a mistake. The etymology derives from the Latin term 'errare', meaning 'to stray'. In statistics, "error" refers to the difference between the value which has been computed and the correct value. An error could result in failure or in a deviation from the intended performance or behavior. Human behavior One reference differentiates between "error" and "mistake" as follows: In human behavior the norms or expectations for behavior or its consequences can be derived from the intention of the actor or from the expectations of other individuals or from a social grouping or from social norms. (See deviance.) Gaffes and faux pas can be labels for certain instances of this kind of error. More serious departures from social norms carry labels such as misbehavior and labels from the legal system, such as misdemeanor and crime. Departures ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
