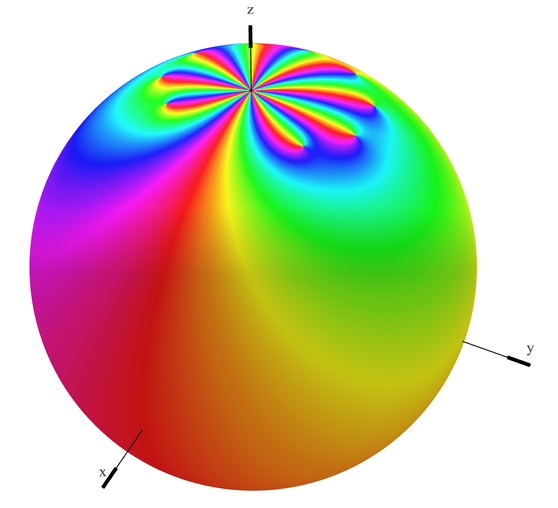
|
Dixon Elliptic Functions
In mathematics, the Dixon elliptic functions sm and cm are two elliptic functions (doubly periodic meromorphic functions on the complex plane) that map from each regular hexagon in a hexagonal tiling to the whole complex plane. Because these functions satisfy the identity \operatorname^3 z + \operatorname^3 z = 1, as real functions they parametrize the cubic Fermat curve x^3 + y^3 = 1, just as the trigonometric functions sine and cosine parametrize the unit circle x^2 + y^2 = 1. They were named sm and cm by Alfred Dixon in 1890, by analogy to the trigonometric functions sine and cosine and the Jacobi elliptic functions sn and cn; Göran Dillner described them earlier in 1873. Definition The functions sm and cm can be defined as the solutions to the initial value problem: :\frac \operatorname z = -\operatorname^2 z,\ \frac \operatorname z = \operatorname^2 z,\ \operatorname(0) = 1,\ \operatorname(0) = 0 Or as the inverse of the Schwarz–Christoffel mapping from the complex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dixon Cm, Sm Functions
Dixon may refer to: Places International * Dixon Entrance, part of the Inside Passage between Alaska and British Columbia Canada * Dixon, Ontario United States * Dixon, California * Dixon, Illinois * Dixon, Greene County, Indiana * Dixon, Indiana and Ohio, an unincorporated community in Allen County, Indiana and Van Wert County, Ohio * Dixon, Iowa * Dixon, Kentucky * Dixon, New Orleans * Dixon, Michigan * Dixon, Missouri * Dixon, Montana * Dixon, Nebraska * Dixon, New Mexico * Dixon, South Dakota * Dixon, Wyoming * Dixon County, Nebraska * Dixon Lane-Meadow Creek, California Other * Dixons Creek, Victoria, Australia Other uses * Dixon (surname) * Dixon (DJ) (born 1975), German house and techno DJ and producer * Dixon, drummer in an early line-up of Siouxsie and the Banshees * ''Dixon of Dock Green'', BBC TV police series * Dixon Ticonderoga, a pencil manufacturer * Dixon (Shacklefords, Virginia) * USS ''Dixon'' (AS-37), a U.S. Navy submarine tender See also * Dickson (di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conformal Map Projection From Globe To Octahedron , in cartography
{{disambig ...
Conformal may refer to: * Conformal (software), in ASIC Software * Conformal coating in electronics * Conformal cooling channel, in injection or blow moulding * Conformal field theory in physics, such as: ** Boundary conformal field theory ** Coset conformal field theory ** Logarithmic conformal field theory ** Rational conformal field theory * Conformal fuel tanks on military aircraft * Conformal hypergraph, in mathematics * Conformal geometry, in mathematics * Conformal group, in mathematics * Conformal map, in mathematics * Conformal map projection In cartography, a conformal map projection is one in which every angle between two curves that cross each other on Earth (a sphere or an ellipsoid) is preserved in the image of the projection, i.e. the projection is a conformal map in the mathema ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arthur Cayley
Arthur Cayley (; 16 August 1821 – 26 January 1895) was a prolific United Kingdom of Great Britain and Ireland, British mathematician who worked mostly on algebra. He helped found the modern British school of pure mathematics. As a child, Cayley enjoyed solving complex maths problems for amusement. He entered Trinity College, Cambridge, where he excelled in Greek language, Greek, French language, French, German language, German, and Italian language, Italian, as well as mathematics. He worked as a lawyer for 14 years. He postulated the Cayley–Hamilton theorem—that every square matrix is a root of its own characteristic polynomial, and verified it for matrices of order 2 and 3. He was the first to define the concept of a group (mathematics), group in the modern way—as a set with a Binary function, binary operation satisfying certain laws. Formerly, when mathematicians spoke of "groups", they had meant permutation groups. Cayley tables and Cayley graphs as well as Cayle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lattice (group)
In geometry and group theory, a lattice in the real coordinate space \mathbb^n is an infinite set of points in this space with the properties that coordinate wise addition or subtraction of two points in the lattice produces another lattice point, that the lattice points are all separated by some minimum distance, and that every point in the space is within some maximum distance of a lattice point. Closure under addition and subtraction means that a lattice must be a subgroup of the additive group of the points in the space, and the requirements of minimum and maximum distance can be summarized by saying that a lattice is a Delone set. More abstractly, a lattice can be described as a free abelian group of dimension n which spans the vector space \mathbb^n. For any basis of \mathbb^n, the subgroup of all linear combinations with integer coefficients of the basis vectors forms a lattice, and every lattice can be formed from a basis in this way. A lattice may be viewed as a regula ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Weierstrass Elliptic Functions
In mathematics, the Weierstrass elliptic functions are elliptic functions that take a particularly simple form. They are named for Karl Weierstrass. This class of functions are also referred to as ℘-functions and they are usually denoted by the symbol ℘, a uniquely fancy script ''p''. They play an important role in the theory of elliptic functions. A ℘-function together with its derivative can be used to parameterize elliptic curves and they generate the field of elliptic functions with respect to a given period lattice. Symbol for Weierstrass \wp-function Definition Let \omega_1,\omega_2\in\mathbb be two complex numbers that are linearly independent over \mathbb and let \Lambda:=\mathbb\omega_1+\mathbb\omega_2:=\ be the lattice generated by those numbers. Then the \wp-function is defined as follows: \weierp(z,\omega_1,\omega_2):=\weierp(z,\Lambda) := \frac + \sum_\left(\frac 1 - \frac 1 \right). This series converges locally uniformly absolutely in \mathb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Weierstrass Cubic Curve Related To The Dixon Elliptic Functions
Karl Theodor Wilhelm Weierstrass (german: link=no, Weierstraß ; 31 October 1815 – 19 February 1897) was a German mathematician often cited as the "father of modern analysis". Despite leaving university without a degree, he studied mathematics and trained as a school teacher, eventually teaching mathematics, physics, botany and gymnastics. He later received an honorary doctorate and became professor of mathematics in Berlin. Among many other contributions, Weierstrass formalized the definition of the continuity of a function, proved the intermediate value theorem and the Bolzano–Weierstrass theorem, and used the latter to study the properties of continuous functions on closed bounded intervals. Biography Weierstrass was born into a Roman Catholic family in Ostenfelde, a village near Ennigerloh, in the Province of Westphalia. Weierstrass was the son of Wilhelm Weierstrass, a government official, and Theodora Vonderforst both of whom were catholic Rhinelanders. His inter ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eisenstein Integer
In mathematics, the Eisenstein integers (named after Gotthold Eisenstein), occasionally also known as Eulerian integers (after Leonhard Euler), are the complex numbers of the form :z = a + b\omega , where and are integers and :\omega = \frac = e^ is a primitive (hence non-real) cube root of unity. The Eisenstein integers form a triangular lattice in the complex plane, in contrast with the Gaussian integers, which form a square lattice in the complex plane. The Eisenstein integers are a countably infinite set. Properties The Eisenstein integers form a commutative ring of algebraic integers in the algebraic number field \mathbb(\omega) — the third cyclotomic field. To see that the Eisenstein integers are algebraic integers note that each is a root of the monic polynomial :z^2 - (2a - b)\;\!z + \left(a^2 - ab + b^2\right)~. In particular, satisfies the equation :\omega^2 + \omega + 1 = 0~. The product of two Eisenstein integers and is given explicitly by :(a + ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Root Of Unity
In mathematics, a root of unity, occasionally called a Abraham de Moivre, de Moivre number, is any complex number that yields 1 when exponentiation, raised to some positive integer power . Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, and the discrete Fourier transform. Roots of unity can be defined in any field (mathematics), field. If the characteristic of a field, characteristic of the field is zero, the roots are complex numbers that are also algebraic integers. For fields with a positive characteristic, the roots belong to a finite field, and, converse (logic), conversely, every nonzero element of a finite field is a root of unity. Any algebraically closed field contains exactly th roots of unity, except when is a multiple of the (positive) characteristic of the field. General definition An ''th root of unity'', where is a positive integer, is a number satisfying the equation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zeros And Poles
In complex analysis (a branch of mathematics), a pole is a certain type of singularity of a complex-valued function of a complex variable. In some sense, it is the simplest type of singularity. Technically, a point is a pole of a function if it is a zero of the function and is holomorphic in some neighbourhood of (that is, complex differentiable in a neighbourhood of ). A function is meromorphic in an open set if for every point of there is a neighborhood of in which either or is holomorphic. If is meromorphic in , then a zero of is a pole of , and a pole of is a zero of . This induces a duality between ''zeros'' and ''poles'', that is fundamental for the study of meromorphic functions. For example, if a function is meromorphic on the whole complex plane plus the point at infinity, then the sum of the multiplicities of its poles equals the sum of the multiplicities of its zeros. Definitions A function of a complex variable is holomorphic in an open domai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Green's Theorem
In vector calculus, Green's theorem relates a line integral around a simple closed curve to a double integral over the plane region bounded by . It is the two-dimensional special case of Stokes' theorem. Theorem Let be a positively oriented, piecewise smooth, simple closed curve in a plane, and let be the region bounded by . If and are functions of defined on an open region containing and have continuous partial derivatives there, then \oint_C (L\, dx + M\, dy) = \iint_ \left(\frac - \frac\right) dx\, dy where the path of integration along is anticlockwise. In physics, Green's theorem finds many applications. One is solving two-dimensional flow integrals, stating that the sum of fluid outflowing from a volume is equal to the total outflow summed about an enclosing area. In plane geometry, and in particular, area surveying, Green's theorem can be used to determine the area and centroid of plane figures solely by integrating over the perimeter. Proof when ''D'' is a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |