|
Dirac Semimetal
Dirac cones, named after Paul Dirac, are features that occur in some electronic band structures that describe unusual electron transport properties of materials like graphene and topological insulators. In these materials, at energies near the Fermi level, the valence band and conduction band take the shape of the upper and lower halves of a conical surface, meeting at what are called Dirac points. Description In quantum mechanics, Dirac cones are a kind of crossing-point which electrons avoid, where the energy of the valence and conduction bands are not equal anywhere in two dimensional lattice -space, except at the zero dimensional Dirac points. As a result of the cones, electrical conduction can be described by the movement of charge carriers which are massless fermions, a situation which is handled theoretically by the relativistic Dirac equation. The massless fermions lead to various quantum Hall effects, magnetoelectric effects in topological materials, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Graphene Brillouin Zone & Linear Dispersion
Graphene () is an allotrope of carbon consisting of a single layer of atoms arranged in a hexagonal lattice nanostructure. "Carbon nanostructures for electromagnetic shielding applications", Mohammed Arif Poothanari, Sabu Thomas, et al., ''Industrial Applications of Nanomaterials'', 2019. "Carbon nanostructures include various low-dimensional allotropes of carbon including carbon black (CB), carbon fiber, carbon nanotubes (CNTs), fullerene, and graphene." The name is derived from "graphite" and the suffix , reflecting the fact that the allotrope of carbon contains numerous double bonds. Each ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Quantum Hall Effect
The quantum Hall effect (or integer quantum Hall effect) is a quantized version of the Hall effect which is observed in two-dimensional electron systems subjected to low temperatures and strong magnetic fields, in which the Hall resistance exhibits steps that take on the quantized values : R_ = \frac = \frac , where is the Hall voltage, is the channel current, is the elementary charge and is Planck's constant. The divisor can take on either integer () or fractional () values. Here, is roughly but not exactly equal to the filling factor of Landau levels. The quantum Hall effect is referred to as the integer or fractional quantum Hall effect depending on whether is an integer or fraction, respectively. The striking feature of the integer quantum Hall effect is the persistence of the quantization (i.e. the Hall plateau) as the electron density is varied. Since the electron density remains constant when the Fermi level is in a clean spectral gap, this situation correspo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Nanophotonics
Nanophotonics or nano-optics is the study of the behavior of light on the nanometer scale, and of the interaction of nanometer-scale objects with light. It is a branch of optics, optical engineering, electrical engineering, and nanotechnology. It often involves dielectric structures such as nanoantennas, or metallic components, which can transport and focus light via surface plasmon polaritons. The term "nano-optics", just like the term "optics", usually refers to situations involving ultraviolet, visible, and near-infrared light (free-space wavelengths from 300 to 1200 nanometers). Background Normal optical components, like lenses and microscopes, generally cannot normally focus light to nanometer (deep subwavelength) scales, because of the diffraction limit (Rayleigh criterion). Nevertheless, it is possible to squeeze light into a nanometer scale using other techniques like, for example, surface plasmons, localized surface plasmons around nanoscale metal objects, and the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Phonon
In physics, a phonon is a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter, specifically in solids and some liquids. A type of quasiparticle, a phonon is an excited state in the quantum mechanical quantization of the modes of vibrations for elastic structures of interacting particles. Phonons can be thought of as quantized sound waves, similar to photons as quantized light waves. The study of phonons is an important part of condensed matter physics. They play a major role in many of the physical properties of condensed matter systems, such as thermal conductivity and electrical conductivity, as well as in models of neutron scattering and related effects. The concept of phonons was introduced in 1932 by Soviet physicist Igor Tamm. The name ''phonon'' comes from the Greek word (), which translates to ''sound'' or ''voice'', because long-wavelength phonons give rise to sound. The name is analogous to the word ''photon''. Definiti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
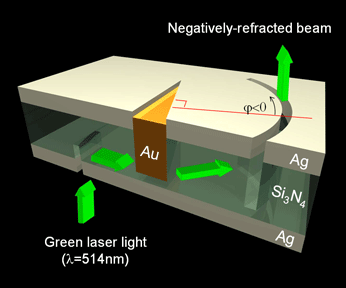 |
Plasmonics
Plasmonics or nanoplasmonics refers to the generation, detection, and manipulation of signals at optical frequencies along metal-dielectric interfaces in the nanometer scale. Inspired by photonics, plasmonics follows the trend of miniaturizing optical devices (see also nanophotonics), and finds applications in sensing, microscopy, optical communications, and bio-photonics. Principles Plasmonics typically utilizes so-called surface plasmon polaritons (SPPs), that are coherent electron oscillations travelling together with an electromagnetic wave along the interface between a dielectric (e.g. glass, air) and a metal (e.g. silver, gold). The SPP modes are strongly confined to their supporting interface, giving rise to strong light-matter interactions. In particular, the electron gas in the metal oscillates with the electro-magnetic wave. Because the moving electrons are scattered, ohmic losses in plasmonic signals are generally large, which limits the signal transfer distances to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
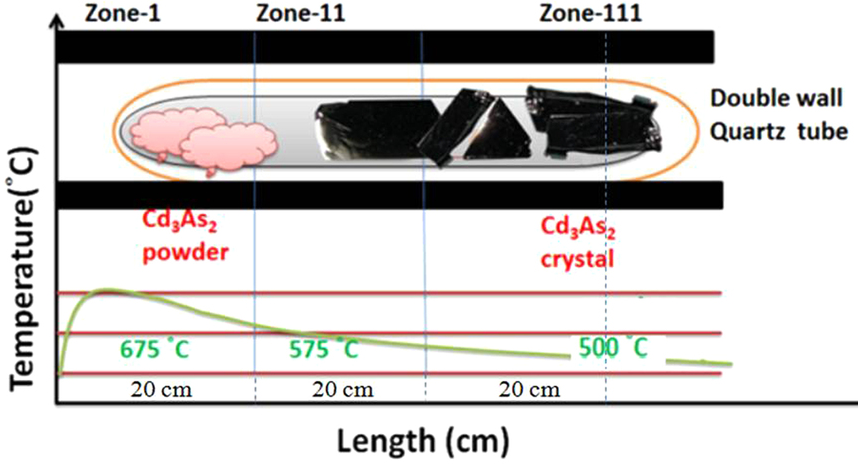 |
Cadmium Arsenide
Cadmium arsenide ( Cd3 As2) is an inorganic semimetal in the II-V family. It exhibits the Nernst effect. Properties Thermal Cd3As2 dissociates between 220 and 280 °C according to the reaction :2 Cd3As2(s) → 6 Cd(g) + As4(g) An energy barrier was found for the nonstoichiometric vaporization of arsenic due to the irregularity of the partial pressures with temperature. The range of the energy gap is from 0.5 to 0.6 eV. Cd3As2 melts at 716 °C and changes phase at 615 °C/ Phase transition Pure cadmium arsenide undergoes several phase transitions at high temperatures, making phases labeled α (stable), α’, α” (metastable), and β. At 593° the polymorphic transition α → β occurs. :α-Cd3As2 ↔ α’-Cd3As2 occurs at ~500 K. :α’-Cd3As2 ↔ α’’-Cd3As2 occurs at ~742 K and is a regular first order phase transition with marked hysteresis loop. :α”-Cd3As2 ↔ β-Cd3As2 occurs at 868 K. Single crystal x-ray diffraction was used to d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Weyl Semimetal
Weyl fermions are massless chiral fermions embodying the mathematical concept of a Weyl spinor. Weyl spinors in turn play an important role in quantum field theory and the Standard Model, where they are a building block for fermions in quantum field theory. Weyl spinors are a solution to the Dirac equation derived by Hermann Weyl, called the Weyl equation. For example, one-half of a charged Dirac fermion of a definite chirality is a Weyl fermion. Weyl fermions may be realized as emergent quasiparticles in a low-energy condensed matter system. This prediction was first proposed by Conyers Herring in 1937, in the context of electronic band structures of solid state systems such as electronic crystals. Topological materials in the vicinity of band inversion transition became a primary target in search of topologically protected bulk electronic band crossings. The first (non-electronic) liquid state which is suggested, has similarly emergent but neutral excitation and theoret ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Hypercone
In geometry, a hypercone (or spherical cone) is the figure in the 4-dimensional Euclidean space represented by the equation :x^2 + y^2 + z^2 - w^2 = 0. It is a quadric surface, and is one of the possible 3-manifolds which are 4-dimensional equivalents of the conical surface in 3 dimensions. It is also named "spherical cone" because its intersections with hyperplanes perpendicular to the ''w''-axis are spheres. A four-dimensional right hypercone can be thought of as a sphere which expands with time, starting its expansion from a single point source, such that the center of the expanding sphere remains fixed. An oblique hypercone would be a sphere which expands with time, again starting its expansion from a point source, but such that the center of the expanding sphere moves with a uniform velocity. Parametric form A right spherical hypercone can be described by the function : \vec \sigma (\phi, \theta, t) = (t s \cos \theta \cos \phi, t s \cos \theta \sin \phi, t s \sin \theta ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
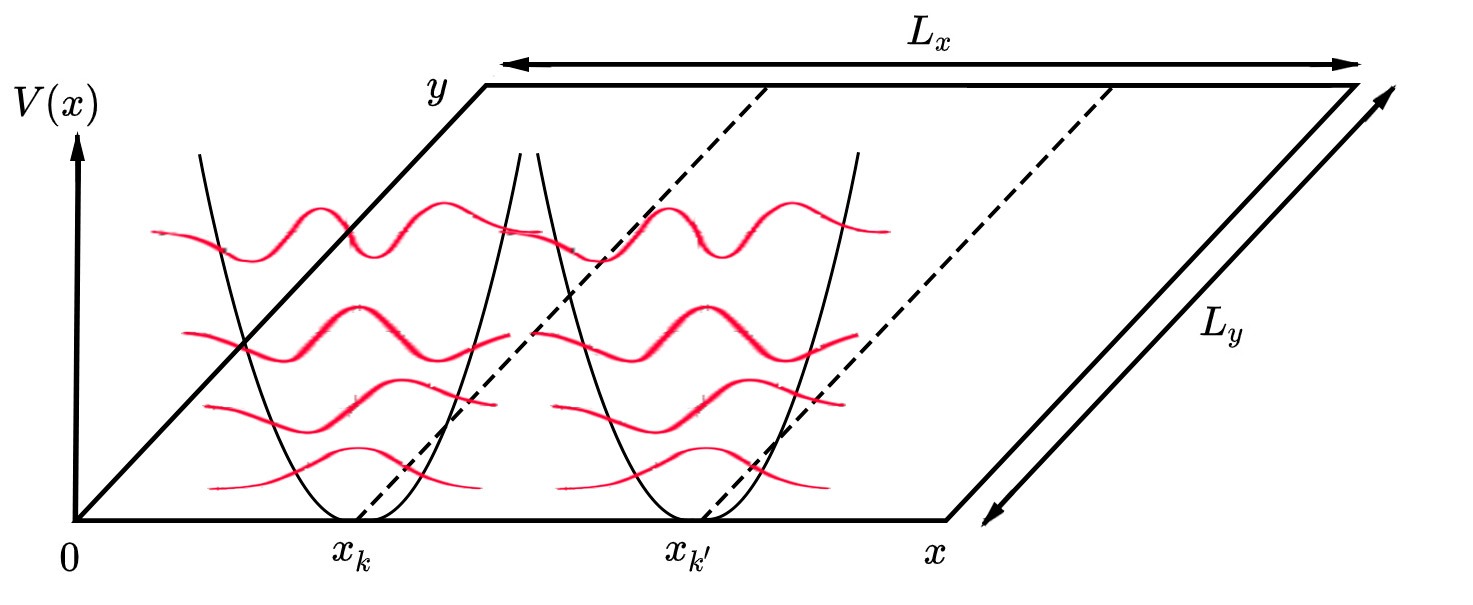
Crystal Momentum
In solid-state physics crystal momentum or quasimomentum is a momentum-like vector associated with electrons in a crystal lattice. It is defined by the associated wave vectors \mathbf of this lattice, according to :_ \equiv \hbar (where \hbar is the reduced Planck's constant). Frequently, crystal momentum is conserved like mechanical momentum, making it useful to physicists and materials scientists as an analytical tool. Lattice symmetry origins A common method of modeling crystal structure and behavior is to view electrons as quantum mechanical particles traveling through a fixed infinite periodic potential V(x) such that :V(+)=V(), where \mathbf is an arbitrary lattice vector. Such a model is sensible because crystal ions that form the lattice structure are typically on the order of tens of thousands of times more massive than electrons, making it safe to replace them with a fixed potential structure, and the macroscopic dimensions of a crystal are typically far greater th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Dispersion Relation
In the physical sciences and electrical engineering, dispersion relations describe the effect of dispersion on the properties of waves in a medium. A dispersion relation relates the wavelength or wavenumber of a wave to its frequency. Given the dispersion relation, one can calculate the phase velocity and group velocity of waves in the medium, as a function of frequency. In addition to the geometry-dependent and material-dependent dispersion relations, the overarching Kramers–Kronig relations describe the frequency dependence of wave propagation and attenuation. Dispersion may be caused either by geometric boundary conditions ( waveguides, shallow water) or by interaction of the waves with the transmitting medium. Elementary particles, considered as matter waves, have a nontrivial dispersion relation even in the absence of geometric constraints and other media. In the presence of dispersion, wave velocity is no longer uniquely defined, giving rise to the distinction ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
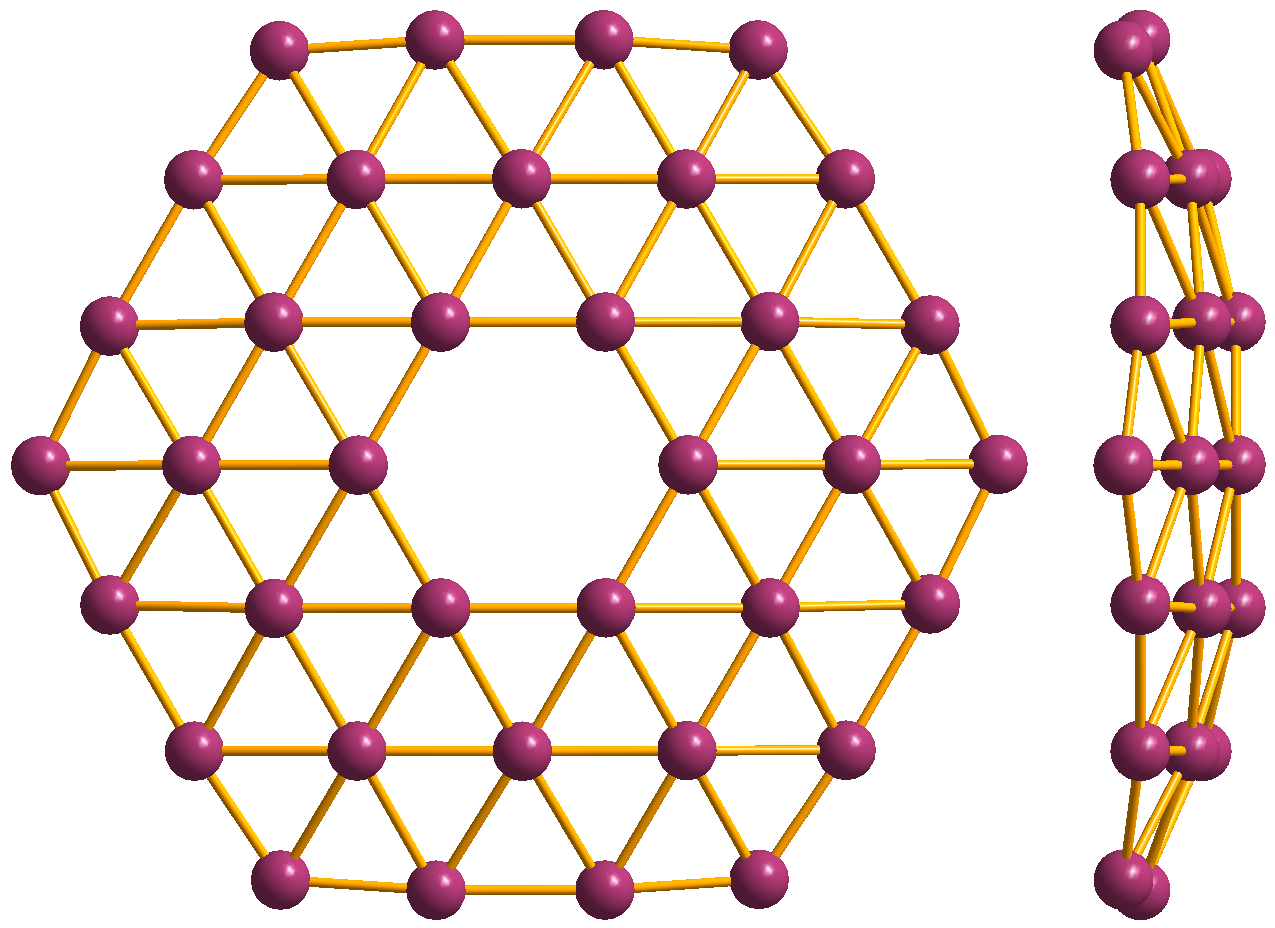 |
Two-dimensional Materials
In materials science, the term single-layer materials or 2D materials refers to crystalline solids consisting of a single layer of atoms. These materials are promising for some applications but remain the focus of research. Single-layer materials derived from single elements generally carry the -ene suffix in their names, e.g. graphene. Single-layer materials that are compounds of two or more elements have -ane or -ide suffixes. 2D materials can generally be categorized as either 2D allotropes of various elements or as compounds (consisting of two or more covalently bonding elements). It is predicted that there are hundreds of stable single-layer materials. The atomic structure and calculated basic properties of these and many other potentially synthesisable single-layer materials, can be found in computational databases. 2D materials can be produced using mainly two approaches: top-down exfoliation and bottom-up synthesis. The exfoliation methods include sonication, mechanical, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Graphite Intercalation Compound
Graphite intercalation compounds are complex materials having a formula where the ion or is inserted ( intercalated) between the oppositely charged carbon layers. Typically ''m'' is much less than 1. These materials are deeply colored solids that exhibit a range of electrical and redox properties of potential applications. Preparation and structure These materials are prepared by treating graphite with a strong oxidant or a strong reducing agent: : The reaction is reversible. The host (graphite) and the guest X interact by charge transfer. An analogous process is the basis of commercial lithium-ion batteries. In a graphite intercalation compound not every layer is necessarily occupied by guests. In so-called ''stage 1 compounds'', graphite layers and intercalated layers alternate and in ''stage 2 compounds'', two graphite layers with no guest material in between alternate with an intercalated layer. The actual composition may vary and therefore these compounds are an example ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |