|
Differential Algebraic Equation
In electrical engineering, a differential-algebraic system of equations (DAEs) is a system of equations that either contains differential equations and algebraic equations, or is equivalent to such a system. In mathematics these are examples of ``differential algebraic varieties'' and correspond to ideals in differential polynomial rings (see the article on differential algebra for the algebraic setup. We can write these differential equations for a dependent vector of variables ''x'' in one independent variable ''t'', as ::F(\dot x(t),\, x(t),\,t)=0 When considering these symbols as functions of a real variable (as is the case in applications in electrical engineering or control theory) we look at x: ,bto\R^n as a vector of dependent variables x(t)=(x_1(t),\dots,x_n(t)) and the system has as many equations, which we consider as functions F=(F_1,\dots,F_n):\R^\to\R^n. They are distinct from ordinary differential equation (ODE) in that a DAE is not completely solvable for the deri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electrical Engineering
Electrical engineering is an engineering discipline concerned with the study, design, and application of equipment, devices, and systems which use electricity, electronics, and electromagnetism. It emerged as an identifiable occupation in the latter half of the 19th century after commercialization of the electric telegraph, the telephone, and electrical power generation, distribution, and use. Electrical engineering is now divided into a wide range of different fields, including computer engineering, systems engineering, power engineering, telecommunications, radio-frequency engineering, signal processing, instrumentation, photovoltaic cells, electronics, and optics and photonics. Many of these disciplines overlap with other engineering branches, spanning a huge number of specializations including hardware engineering, power electronics, electromagnetics and waves, microwave engineering, nanotechnology, electrochemistry, renewable energies, mechatronics/control, and electrical m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
SPICE
A spice is a seed, fruit, root, bark, or other plant substance primarily used for flavoring or coloring food. Spices are distinguished from herbs, which are the leaves, flowers, or stems of plants used for flavoring or as a garnish. Spices are sometimes used in medicine, religious rituals, cosmetics or perfume production. For example, vanilla is commonly used as an ingredient in fragrance manufacturing. A spice may be available in several forms: fresh, whole dried, or pre-ground dried. Generally, spices are dried. Spices may be ground into a powder for convenience. A whole dried spice has the longest shelf life, so it can be purchased and stored in larger amounts, making it cheaper on a per-serving basis. A fresh spice, such as ginger, is usually more flavorful than its dried form, but fresh spices are more expensive and have a much shorter shelf life. Some spices are not always available either fresh or whole, for example turmeric, and often must be purchased in ground form. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebraic Differential Equation
In mathematics, an algebraic differential equation is a differential equation that can be expressed by means of differential algebra. There are several such notions, according to the concept of differential algebra used. The intention is to include equations formed by means of differential operators, in which the coefficients are rational functions of the variables (e.g. the hypergeometric equation). Algebraic differential equations are widely used in computer algebra and number theory. A simple concept is that of a polynomial vector field, in other words a vector field expressed with respect to a standard co-ordinate basis as the first partial derivatives with polynomial coefficients. This is a type of first-order algebraic differential operator. Formulations *Derivations ''D'' can be used as algebraic analogues of the formal part of differential calculus, so that algebraic differential equations make sense in commutative rings. *The theory of differential fields was set u ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
APMonitor
Advanced process monitor (APMonitor) is a modeling language for differential algebraic (DAE) equations. It is a free web-service or local server for solving representations of physical systems in the form of implicit DAE models. APMonitor is suited for large-scale problems and solves linear programming, integer programming, nonlinear programming, nonlinear mixed integer programming, dynamic simulation, moving horizon estimation, and nonlinear model predictive control. APMonitor does not solve the problems directly, but calls nonlinear programming solvers such as APOPT, BPOPT, IPOPT, MINOS, and SNOPT. The APMonitor API provides exact first and second derivatives of continuous functions to the solvers through automatic differentiation and in sparse matrix form. Programming language integration Julia, MATLAB, Python are mathematical programming languages that have APMonitor integration through web-service APIs. The GEKKO Optimization Suite is a recent extension of APMonitor wi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dummy Derivative Index Reduction Method
Dummy may refer to: Dolls * Mannequin, a model of the human body * Dummy (ventriloquism) * Crash test dummy People * Dummy (nickname), any of several people with the nickname * Dummy, the Witch of Sible Hedingham (c. 1788–1863), one of the last people to be accused of being a witch in England Arts and entertainment Characters * Dummy (Marvel Comics), from the comic book ''X-Men'' * Dummy (DC Comics) Films * ''Dummy'' (1979 film), a TV movie starring LeVar Burton and Paul Sorvino * ''Dummy'' (2002 film), a comedy/drama * ''Dummy'', a 2009 coming-of-age drama starring Emma Catherwood * ''Dummy'', a short film by Kira Muratova * ''The Dummy'' (1917 film), an American silent drama * ''The Dummy'' (1929 film), an American comedy Music * ''Dummy'' (album), 1994, by Portishead * "Dummy!", a song by Toby Fox from the soundtrack of the 2015 video game ''Undertale'' Television * "Dummy" (''Pushing Daisies'' episode) * "The Dummy", an episode of ''The Twilight Zone'' * ''Dum ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pantelides Algorithm
Pantelides algorithm in mathematics is a systematic method for reducing high-index systems of differential-algebraic equations to lower index. This is accomplished by selectively adding differentiated forms of the equations already present in the system. It is possible for the algorithm to fail in some instances. Pantelides algorithm is implemented in several significant equation-based simulation programs such as gPROMS, Modelica Modelica is an object-oriented, declarative, multi-domain modeling language for component-oriented modeling of complex systems, e.g., systems containing mechanical, electrical, electronic, hydraulic, thermal, control, electric power or process-o ... and EMSO. a free-to-use closed-source simulator/equation solver that includes implementation for the Pantelides algorithm. References [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebraic Equations
In mathematics Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics ..., an algebraic equation or polynomial equation is an equation of the form :P = 0 where ''P'' is a polynomial with coefficients in some field (mathematics), field, often the field of the rational numbers. For many authors, the term ''algebraic equation'' refers only to ''univariate equations'', that is polynomial equations that involve only one variable (mathematics), variable. On the other hand, a polynomial equation may involve several variables. In the case of several variables (the ''multivariate'' case), the term ''polynomial equation'' is usually preferred to ''algebraic equation''. For example, :x^5-3x+1=0 is an algebraic equation with integer coefficients and :y^4 + \frac - \frac + xy^2 + y^2 + \frac = 0 is a m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ordinary Differential Equations
In mathematics, an ordinary differential equation (ODE) is a differential equation whose unknown(s) consists of one (or more) function(s) of one variable and involves the derivatives of those functions. The term ''ordinary'' is used in contrast with the term partial differential equation which may be with respect to ''more than'' one independent variable. Differential equations A linear differential equation is a differential equation that is defined by a linear polynomial in the unknown function and its derivatives, that is an equation of the form :a_0(x)y +a_1(x)y' + a_2(x)y'' +\cdots +a_n(x)y^+b(x)=0, where , ..., and are arbitrary differentiable functions that do not need to be linear, and are the successive derivatives of the unknown function of the variable . Among ordinary differential equations, linear differential equations play a prominent role for several reasons. Most elementary and special functions that are encountered in physics and applied mathematics are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
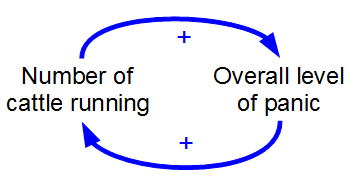
Positive Feedback
Positive feedback (exacerbating feedback, self-reinforcing feedback) is a process that occurs in a feedback loop which exacerbates the effects of a small disturbance. That is, the effects of a perturbation on a system include an increase in the magnitude of the perturbation. That is, ''A produces more of B which in turn produces more of A''.Keesing, R.M. (1981). Cultural anthropology: A contemporary perspective (2nd ed.) p.149. Sydney: Holt, Rinehard & Winston, Inc. In contrast, a system in which the results of a change act to reduce or counteract it has negative feedback. Both concepts play an important role in science and engineering, including biology, chemistry, and cybernetics. Mathematically, positive feedback is defined as a positive loop gain around a closed loop of cause and effect. That is, positive feedback is Phase (waves), in phase with the input, in the sense that it adds to make the input larger. Positive feedback tends to cause Control theory#Stability, system i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Operational Amplifiers
An operational amplifier (often op amp or opamp) is a DC-coupled high-gain electronic voltage amplifier with a differential input and, usually, a single-ended output. In this configuration, an op amp produces an output potential (relative to circuit ground) that is typically 100,000 times larger than the potential difference between its input terminals. The operational amplifier traces its origin and name to analog computers, where they were used to perform mathematical operations in linear, non-linear, and frequency-dependent circuits. The popularity of the op amp as a building block in analog circuits is due to its versatility. By using negative feedback, the characteristics of an op-amp circuit, its gain, input and output impedance, bandwidth etc. are determined by external components and have little dependence on temperature coefficients or engineering tolerance in the op amp itself. Op amps are used widely in electronic devices today, including a vast array of consumer, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Netlist
In electronic design, a netlist is a description of the connectivity of an electronic circuit. In its simplest form, a netlist consists of a list of the electronic components in a circuit and a list of the nodes they are connected to. A network (net) is a collection of two or more interconnected components. The structure, complexity and representation of netlists can vary considerably, but the fundamental purpose of every netlist is to convey connectivity information. Netlists usually provide nothing more than instances, nodes, and perhaps some attributes of the components involved. If they express much more than this, they are usually considered to be a hardware description language such as Verilog or VHDL, or one of several languages specifically designed for input to simulators or hardware compilers (such as SPICE analog simulation netlists). Types of netlists Netlists can be: * Physical (based upon physical connections) or logical (based upon logical connections) ** For ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
