|
Diagnostic Equation
In a physical (and especially geophysical) simulation context, a diagnostic equation (or diagnostic model) is an equation (or model) that links the values of these variables simultaneously, either because the equation (or model) is time-independent, or because the variables all refer to the values they have at the identical time. This is by opposition to a prognostic equation. For instance, the so-called ideal gas law (''PV'' = ''nRT'') of classical thermodynamics relates the state variable A state variable is one of the set of variables that are used to describe the mathematical "state" of a dynamical system. Intuitively, the state of a system describes enough about the system to determine its future behaviour in the absence of a ...s of that gas, all estimated at the same time. It is understood that the values of any one of these variables can change in time, but the relation between these variables will remain valid at each and every particular instant, which implies that one ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prognostic Equation
Prognostic equation - in the context of physical (and especially geophysical) simulation, a prognostic equation predicts the value of variables for some time in the future on the basis of the values at the current or previous times. For instance, the well-known Navier-Stokes equations that describe the time evolution of a fluid are prognostic equations that predict the future distribution of velocities in that fluid on the basis of current fields such as the pressure gradient. See also *diagnostic equation In a physical (and especially geophysical) simulation context, a diagnostic equation (or diagnostic model) is an equation (or model) that links the values of these variables simultaneously, either because the equation (or model) is time-independent, ... References James R. Holton (2004) ''An Introduction to Dynamic Meteorology'', Academic Press, International Geophysics Series Volume 88, Fourth Edition, 535 p., , {{ISBN, 978-0-12-354015-7. See also http://glossary.ametsoc. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
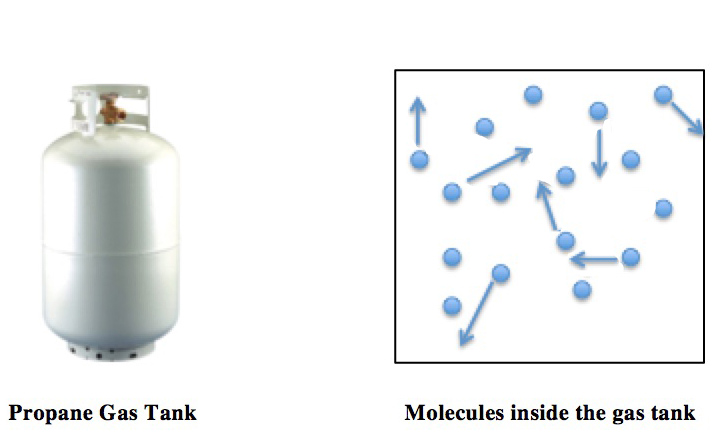
Ideal Gas Law
The ideal gas law, also called the general gas equation, is the equation of state of a hypothetical ideal gas. It is a good approximation of the behavior of many gases under many conditions, although it has several limitations. It was first stated by Benoît Paul Émile Clapeyron in 1834 as a combination of the empirical Boyle's law, Charles's law, Avogadro's law, and Gay-Lussac's law. The ideal gas law is often written in an empirical form: pV = nRT where p, V and T are the pressure, volume and temperature; n is the amount of substance; and R is the ideal gas constant. It can also be derived from the microscopic kinetic theory, as was achieved (apparently independently) by August Krönig in 1856 and Rudolf Clausius in 1857. Equation The state of an amount of gas is determined by its pressure, volume, and temperature. The modern form of the equation relates these simply in two main forms. The temperature used in the equation of state is an absolute temperature: the appropria ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thermodynamics
Thermodynamics is a branch of physics that deals with heat, work, and temperature, and their relation to energy, entropy, and the physical properties of matter and radiation. The behavior of these quantities is governed by the four laws of thermodynamics which convey a quantitative description using measurable macroscopic physical quantities, but may be explained in terms of microscopic constituents by statistical mechanics. Thermodynamics applies to a wide variety of topics in science and engineering, especially physical chemistry, biochemistry, chemical engineering and mechanical engineering, but also in other complex fields such as meteorology. Historically, thermodynamics developed out of a desire to increase the efficiency of early steam engines, particularly through the work of French physicist Sadi Carnot (1824) who believed that engine efficiency was the key that could help France win the Napoleonic Wars. Scots-Irish physicist Lord Kelvin was the first to formulate a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
State Variable
A state variable is one of the set of variables that are used to describe the mathematical "state" of a dynamical system. Intuitively, the state of a system describes enough about the system to determine its future behaviour in the absence of any external forces affecting the system. Models that consist of coupled first-order differential equations are said to be in state-variable form. Examples *In mechanical systems, the position coordinates and velocities of mechanical parts are typical state variables; knowing these, it is possible to determine the future state of the objects in the system. *In thermodynamics, a state variable is an independent variable of a state function. Examples include internal energy, enthalpy, temperature, pressure, volume and entropy. Heat and work are not state functions, but process functions. *In electronic/electrical circuits, the voltages of the nodes and the currents through components in the circuit are usually the state variables. In any el ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |