|
Dephasing Rate SP Formula
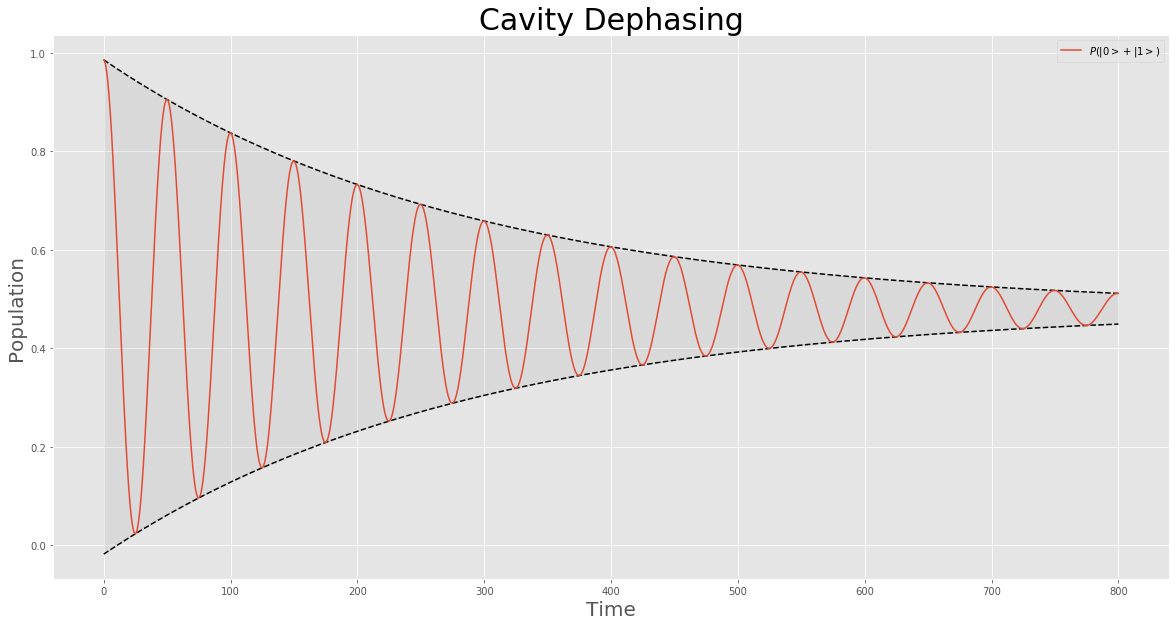
The ''SP'' formula for the dephasing rate \Gamma_ of a particle that moves in a fluctuating environment unifies various results that have been obtained, notably in condensed matter physics, with regard to the motion of electrons in a metal. The general case requires to take into account not only the temporal correlations but also the spatial correlations of the environmental fluctuations. These can be characterized by the spectral form factor \tilde(q,\omega), while the motion of the particle is characterized by its power spectrum \tilde(q,\omega). Consequently, at finite temperature the expression for the dephasing rate takes the following form that involves ''S'' and ''P'' functions: \Gamma_ \ = \ \int d \int \frac \,\tilde(,\omega) \, \tilde(-,-\omega) Due to inherent limitations of the semiclassical (stationary phase) approximation, the physically correct procedure is to use the non-symmetrized quantum versions of \tilde(q,\omega) and \tilde(q,\omega). The argument is based ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dephasing
In physics, dephasing is a mechanism that recovers classical physics, classical behaviour from a quantum physics, quantum system. It refers to the ways in which coherence (physics), coherence caused by perturbation decays over time, and the system returns to the state before perturbation. It is an important effect in molecular and atomic spectroscopy, and in the condensed matter physics of mesoscopic devices. The reason can be understood by describing the conduction in metals as a classical phenomenon with quantum effects all embedded into an Effective mass (solid-state physics), effective mass that can be computed quantum mechanically, as also happens to Conductance quantum, resistance that can be seen as a Scattering theory, scattering effect of Valence and conduction bands, conduction electrons. When the temperature is lowered and the dimensions of the device are meaningfully reduced, this classical behaviour should disappear and the laws of quantum mechanics should govern the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Condensed Matter Physics
Condensed matter physics is the field of physics that deals with the macroscopic and microscopic physical properties of matter, especially the solid and liquid State of matter, phases, that arise from electromagnetic forces between atoms and electrons. More generally, the subject deals with condensed phases of matter: systems of many constituents with strong interactions among them. More exotic condensed phases include the superconductivity, superconducting phase exhibited by certain materials at extremely low cryogenic temperatures, the ferromagnetic and antiferromagnetic phases of Spin (physics), spins on crystal lattices of atoms, the Bose–Einstein condensates found in ultracold atomic systems, and liquid crystals. Condensed matter physicists seek to understand the behavior of these phases by experiments to measure various material properties, and by applying the physical laws of quantum mechanics, electromagnetism, statistical mechanics, and other theoretical physics, physic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fermi's Golden Rule
In quantum physics, Fermi's golden rule is a formula that describes the transition rate (the probability of a transition per unit time) from one energy eigenstate of a quantum system to a group of energy eigenstates in a continuum, as a result of a weak Perturbation theory (quantum mechanics), perturbation. This transition rate is effectively independent of time (so long as the strength of the perturbation is independent of time) and is proportional to the strength of the coupling between the initial and final states of the system (described by the square of the Matrix element (physics), matrix element of the perturbation) as well as the density of states. It is also applicable when the final state is discrete, i.e. it is not part of a continuum, if there is some decoherence in the process, like relaxation or collision of the atoms, or like noise in the perturbation, in which case the density of states is replaced by the reciprocal of the decoherence bandwidth. Historical background ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
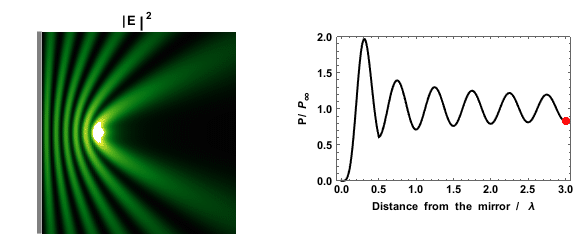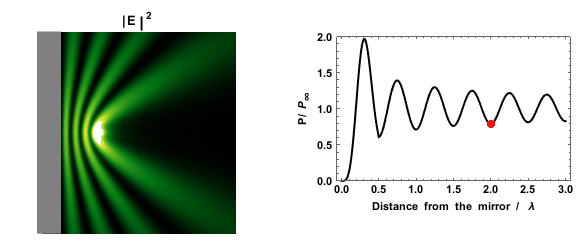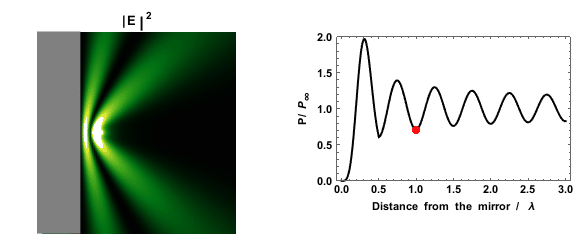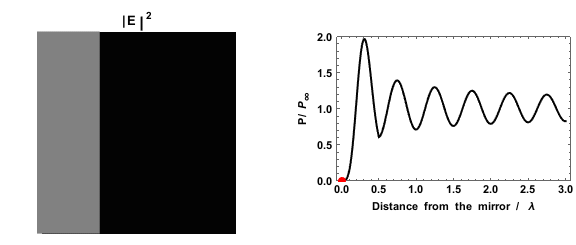
Dissipation Model For Extended Environment
A unified model for ''Diffusion Localization and Dissipation'' (DLD), optionally termed ''Diffusion with Local Dissipation'', has been introduced for the study of ''Quantal Brownian Motion'' (QBM) in dynamical disorder. It can be regarded as a generalization of the familiar Caldeira-Leggett model. \mathcal = \frac + V(x) + \mathcal_ + \mathcal_ \mathcal_=\sum_\left(\frac +\frac m \omega_^2 Q_^2\right) \mathcal_ = - \sum_ c_ Q_ u(x-x_) where Q_ denotes the dynamical coordinate of the \alpha scatterer or bath mode. u(x-x_) is the interaction potential, and c_ are coupling constants. The spectral characterization of the bath is analogous to that of the Caldeira-Leggett model: \frac \sum_ \frac \delta(\omega-\omega_) \ \delta(x-x_) \ = \ J(\omega) i.e. the oscillators that appear in the Hamiltonian are distributed uniformly over space, and in each location have the same spectral distribution J(\omega). Optionally the environment is characterized by the power spectrum of the flu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum State
In quantum physics, a quantum state is a mathematical entity that embodies the knowledge of a quantum system. Quantum mechanics specifies the construction, evolution, and measurement of a quantum state. The result is a prediction for the system represented by the state. Knowledge of the quantum state, and the rules for the system's evolution in time, exhausts all that can be known about a quantum system. Quantum states may be defined differently for different kinds of systems or problems. Two broad categories are * wave functions describing quantum systems using position or momentum variables and * the more abstract vector quantum states. Historical, educational, and application-focused problems typically feature wave functions; modern professional physics uses the abstract vector states. In both categories, quantum states divide into pure versus mixed states, or into coherent states and incoherent states. Categories with special properties include stationary states for tim ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Caldeira-Leggett Model
Quantum dissipation is the branch of physics that studies the quantum analogues of the process of irreversible loss of energy observed at the classical level. Its main purpose is to derive the laws of classical dissipation from the framework of quantum mechanics. It shares many features with the subjects of quantum decoherence and quantum theory of measurement. Models The typical approach to describe dissipation is to split the total system in two parts: the quantum system where dissipation occurs, and a so-called environment or bath into which the energy of the former will flow. The way both systems are coupled depends on the details of the microscopic model, and hence, the description of the bath. To include an irreversible flow of energy (i.e., to avoid Poincaré recurrences in which the energy eventually flows back to the system), requires that the bath contain an infinite number of degrees of freedom. Notice that by virtue of the principle of universality, it is expected tha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Classical Limit
The classical limit or correspondence limit is the ability of a physical theory to approximate or "recover" classical mechanics when considered over special values of its parameters. The classical limit is used with physical theories that predict non-classical behavior. Quantum theory A heuristic postulate called the correspondence principle was introduced to quantum theory by Niels Bohr: in effect it states that some kind of continuity argument should apply to the classical limit of quantum systems as the value of the Planck constant normalized by the action of these systems becomes very small. Often, this is approached through "quasi-classical" techniques (cf. WKB approximation). More rigorously, the mathematical operation involved in classical limits is a group contraction, approximating physical systems where the relevant action is much larger than the reduced Planck constant , so the "deformation parameter" / can be effectively taken to be zero (cf. Weyl quantization.) Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |