|
Dependability State Model
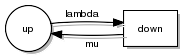
A dependability state diagram is a method for modelling a system as a Markov chain. It is used in reliability engineering for availability and reliability analysis. It consists of creating a finite state machine which represent the different states a system may be in. Transitions between states happen as a result of events from underlying Poisson processes with different intensities. Example A redundant computer system consist of identical two-compute nodes, which each fail with an intensity of \lambda. When failed, they are repaired one at the time by a single repairman with negative exponential distributed repair times with expectation \mu^. * state 0: 0 failed units, normal state of the system. * state 1: 1 failed unit, system operational. * state 2: 2 failed units. system not operational. Intensities from state 0 and state 1 are 2\lambda, since each compute node has a failure intensity of \lambda. Intensity from state 1 to state 2 is \lambda. Transitions from state 2 to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Markov Chain
A Markov chain or Markov process is a stochastic model describing a sequence of possible events in which the probability of each event depends only on the state attained in the previous event. Informally, this may be thought of as, "What happens next depends only on the state of affairs ''now''." A countably infinite sequence, in which the chain moves state at discrete time steps, gives a discrete-time Markov chain (DTMC). A continuous-time process is called a continuous-time Markov chain (CTMC). It is named after the Russian mathematician Andrey Markov. Markov chains have many applications as statistical models of real-world processes, such as studying cruise control systems in motor vehicles, queues or lines of customers arriving at an airport, currency exchange rates and animal population dynamics. Markov processes are the basis for general stochastic simulation methods known as Markov chain Monte Carlo, which are used for simulating sampling from complex probability ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reliability Engineering
Reliability engineering is a sub-discipline of systems engineering that emphasizes the ability of equipment to function without failure. Reliability describes the ability of a system or component to function under stated conditions for a specified period of time. Reliability is closely related to availability, which is typically described as the ability of a component or system to function at a specified moment or interval of time. The reliability function is theoretically defined as the probability of success at time t, which is denoted R(t). This probability is estimated from detailed (physics of failure) analysis, previous data sets or through reliability testing and reliability modelling. Availability, testability, maintainability and maintenance are often defined as a part of "reliability engineering" in reliability programs. Reliability often plays the key role in the cost-effectiveness of systems. Reliability engineering deals with the prediction, prevention and man ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Finite State Machine
A finite-state machine (FSM) or finite-state automaton (FSA, plural: ''automata''), finite automaton, or simply a state machine, is a mathematical model of computation. It is an abstract machine that can be in exactly one of a finite number of '' states'' at any given time. The FSM can change from one state to another in response to some inputs; the change from one state to another is called a ''transition''. An FSM is defined by a list of its states, its initial state, and the inputs that trigger each transition. Finite-state machines are of two types— deterministic finite-state machines and non-deterministic finite-state machines. A deterministic finite-state machine can be constructed equivalent to any non-deterministic one. The behavior of state machines can be observed in many devices in modern society that perform a predetermined sequence of actions depending on a sequence of events with which they are presented. Simple examples are vending machines, which dispense ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Availability
In reliability engineering, the term availability has the following meanings: * The degree to which a system, subsystem or equipment is in a specified operable and committable state at the start of a mission, when the mission is called for at an unknown, ''i.e.'' a random, time. * The probability that an item will operate satisfactorily at a given point in time when used under stated conditions in an ideal support environment. Normally high availability systems might be specified as 99.98%, 99.999% or 99.9996%. Representation The simplest representation of availability (''A'') is a ratio of the expected value of the uptime of a system to the aggregate of the expected values of up and down time (that results in the "total amont of time" ''C'' of the observation window) : A = \frac = \frac Another equation for availability (''A'') is a ratio of the Mean Time To Failure (MTTF) and Mean Time To Repair (MTTR), or : A = \frac = \frac If we define the status function X(t) as : ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
State Explosion Problem
In mathematics, a combinatorial explosion is the rapid growth of the complexity of a problem due to how the combinatorics of the problem is affected by the input, constraints, and bounds of the problem. Combinatorial explosion is sometimes used to justify the intractability of certain problems.http://intelligence.worldofcomputing/combinatorial-explosion Combinatorial Explosion. Examples of such problems include certain mathematical functions, the analysis of some puzzles and games, and some pathological examples which can be modelled as the |
Reliability Engineering
Reliability engineering is a sub-discipline of systems engineering that emphasizes the ability of equipment to function without failure. Reliability describes the ability of a system or component to function under stated conditions for a specified period of time. Reliability is closely related to availability, which is typically described as the ability of a component or system to function at a specified moment or interval of time. The reliability function is theoretically defined as the probability of success at time t, which is denoted R(t). This probability is estimated from detailed (physics of failure) analysis, previous data sets or through reliability testing and reliability modelling. Availability, testability, maintainability and maintenance are often defined as a part of "reliability engineering" in reliability programs. Reliability often plays the key role in the cost-effectiveness of systems. Reliability engineering deals with the prediction, prevention and man ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Markov Models
In probability theory, a Markov model is a stochastic model used to model pseudo-randomly changing systems. It is assumed that future states depend only on the current state, not on the events that occurred before it (that is, it assumes the Markov property). Generally, this assumption enables reasoning and computation with the model that would otherwise be intractable. For this reason, in the fields of predictive modelling and probabilistic forecasting, it is desirable for a given model to exhibit the Markov property. Introduction There are four common Markov models used in different situations, depending on whether every sequential state is observable or not, and whether the system is to be adjusted on the basis of observations made: Markov chain The simplest Markov model is the Markov chain. It models the state of a system with a random variable that changes through time. In this context, the Markov property suggests that the distribution for this variable depends only on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |