|
Dekker's Algorithm
Dekker's algorithm is the first known correct solution to the mutual exclusion problem in concurrent programming where processes only communicate via shared memory. The solution is attributed to Dutch mathematician Th. J. Dekker by Edsger W. Dijkstra in an unpublished paper on sequential process descriptions and his manuscript on cooperating sequential processes. It allows two threads to share a single-use resource without conflict, using only shared memory for communication. It avoids the strict alternation of a naïve turn-taking algorithm, and was one of the first mutual exclusion algorithms to be invented. Overview If two processes attempt to enter a critical section at the same time, the algorithm will allow only one process in, based on whose it is. If one process is already in the critical section, the other process will busy wait for the first process to exit. This is done by the use of two flags, and , which indicate an intention to enter the critical section on t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mutual Exclusion
In computer science, mutual exclusion is a property of concurrency control, which is instituted for the purpose of preventing race conditions. It is the requirement that one thread of execution never enters a critical section while a concurrent thread of execution is already accessing said critical section, which refers to an interval of time during which a thread of execution accesses a shared resource or shared memory. The shared resource is a data object, which two or more concurrent threads are trying to modify (where two concurrent read operations are permitted but, no two concurrent write operations or one read and one write are permitted, since it leads to data inconsistency). Mutual exclusion algorithm ensures that if a process is already performing write operation on a data object ritical sectionno other process/thread is allowed to access/modify the same object until the first process has finished writing upon the data object ritical sectionand released the object ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Memory Ordering
Memory ordering describes the order of accesses to computer memory by a CPU. The term can refer either to the memory ordering generated by the compiler during compile time, or to the memory ordering generated by a CPU during runtime. In modern microprocessors, memory ordering characterizes the CPU's ability to reorder memory operations – it is a type of out-of-order execution. Memory reordering can be used to fully utilize the bus-bandwidth of different types of memory such as caches and memory banks. On most modern uniprocessors memory operations are not executed in the order specified by the program code. In single threaded programs all operations appear to have been executed in the order specified, with all out-of-order execution hidden to the programmer – however in multi-threaded environments (or when interfacing with other hardware via memory buses) this can lead to problems. To avoid problems, memory barriers can be used in these cases. Compile-time memory orderin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Semaphore (programming)
In computer science, a semaphore is a variable or abstract data type used to control access to a common resource by multiple threads and avoid critical section problems in a concurrent system such as a multitasking operating system. Semaphores are a type of synchronization primitive. A trivial semaphore is a plain variable that is changed (for example, incremented or decremented, or toggled) depending on programmer-defined conditions. A useful way to think of a semaphore as used in a real-world system is as a record of how many units of a particular resource are available, coupled with operations to adjust that record ''safely'' (i.e., to avoid race conditions) as units are acquired or become free, and, if necessary, wait until a unit of the resource becomes available. Semaphores are a useful tool in the prevention of race conditions; however, their use is not a guarantee that a program is free from these problems. Semaphores which allow an arbitrary resource count are call ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
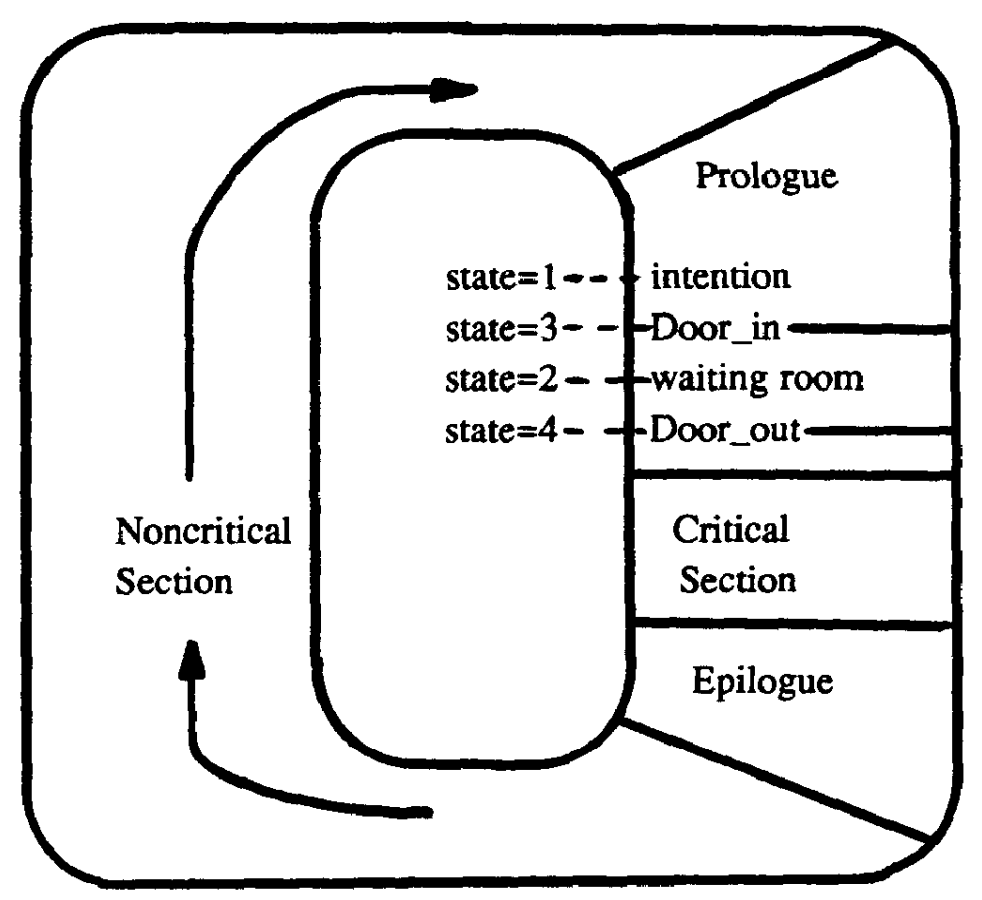
Szymański's Algorithm
Szymański's Mutual Exclusion Algorithm is a mutual exclusion algorithm devised by computer scientist Dr. Bolesław Szymański, which has many favorable properties including linear wait, and which extension solved the open problem posted by Leslie Lamport whether there is an algorithm with a constant number of communication bits per process that satisfies every reasonable fairness and failure-tolerance requirement that Lamport conceived of (Lamport's solution used n factorial communication variables vs. Szymański's 5). The algorithm The algorithm is modeled on a waiting room with an entry and exit doorway. Initially the entry door is open and the exit door is closed. All processes which request entry into the critical section at roughly the same time enter the waiting room; the last of them closes the entry door and opens the exit door. The processes then enter the critical section one by one (or in larger groups if the critical section permits this). The last process to leave ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lamport's Bakery Algorithm
Lamport's bakery algorithm is a computer algorithm devised by computer scientist Leslie Lamport, as part of his long study of the formal correctness of concurrent systems, which is intended to improve the safety in the usage of shared resources among multiple threads by means of mutual exclusion. In computer science, it is common for multiple threads to simultaneously access the same resources. Data corruption can occur if two or more threads try to write into the same memory location, or if one thread reads a memory location before another has finished writing into it. Lamport's bakery algorithm is one of many mutual exclusion algorithms designed to prevent concurrent threads entering critical sections of code concurrently to eliminate the risk of data corruption. Algorithm Analogy Lamport envisioned a bakery with a numbering machine at its entrance so each customer is given a unique number. Numbers increase by one as customers enter the store. A global counter ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Peterson's Algorithm
Peterson's algorithm (or Peterson's solution) is a concurrent programming algorithm for mutual exclusion that allows two or more processes to share a single-use resource without conflict, using only shared memory for communication. It was formulated by Gary L. Peterson in 1981.G. L. Peterson: "Myths About the Mutual Exclusion Problem", ''Information Processing Letters'' 12(3) 1981, 115–116 While Peterson's original formulation worked with only two processes, the algorithm can be generalized for more than two.As discussed in ''Operating Systems Review'', January 1990 ("Proof of a Mutual Exclusion Algorithm", M Hofri). The algorithm The algorithm uses two variables: flag and turn. A flag /code> value of true indicates that the process n wants to enter the critical section. Entrance to the critical section is granted for process P0 if P1 does not want to enter its critical section and if P1 has given priority to P0 by setting turn to 0. The algorithm satisfies the three essenti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eisenberg & McGuire Algorithm
The Eisenberg & McGuire algorithm is an algorithm for solving the critical sections problem, a general version of the dining philosophers problem. It was described in 1972 by Murray A. Eisenberg and Michael R. McGuire. Algorithm All the ''n''-processes share the following variables: enum pstate = ; pstate flags int turn; The variable turn is set arbitrarily to a number between 0 and ''n''−1 at the start of the algorithm. The flags variable for each process is set to WAITING whenever it intends to enter the critical section. flags takes either IDLE or WAITING or ACTIVE. Initially the flags variable for each process is initialized to IDLE. repeat until ((index >= n) && ((turn = i) , , (flags urn= IDLE))); /* Start of CRITICAL SECTION */ /* claim the turn and proceed */ turn := i; /* Critical Section Code of the Process */ /* End of CRITICAL SECTION */ /* find a process which is not IDLE */ /* (if there are no others, we will find ourselv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
C++11
C++11 is a version of the ISO/ IEC 14882 standard for the C++ programming language. C++11 replaced the prior version of the C++ standard, called C++03, and was later replaced by C++14. The name follows the tradition of naming language versions by the publication year of the specification, though it was formerly named ''C++0x'' because it was expected to be published before 2010. Although one of the design goals was to prefer changes to the libraries over changes to the core language, C++11 does make several additions to the core language. Areas of the core language that were significantly improved include multithreading support, generic programming support, uniform initialization, and performance. Significant changes were also made to the C++ Standard Library, incorporating most of the C++ Technical Report 1 (TR1) libraries, except the library of mathematical special functions. C++11 was published as ''ISO/IEC 14882:2011'' in September 2011 and is available for a fee. T ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Memory Barrier
In computing, a memory barrier, also known as a membar, memory fence or fence instruction, is a type of barrier instruction that causes a central processing unit (CPU) or compiler to enforce an ordering constraint on memory operations issued before and after the barrier instruction. This typically means that operations issued prior to the barrier are guaranteed to be performed before operations issued after the barrier. Memory barriers are necessary because most modern CPUs employ performance optimizations that can result in out-of-order execution. This reordering of memory operations (loads and stores) normally goes unnoticed within a single thread of execution, but can cause unpredictable behavior in concurrent programs and device drivers unless carefully controlled. The exact nature of an ordering constraint is hardware dependent and defined by the architecture's memory ordering model. Some architectures provide multiple barriers for enforcing different ordering constrai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Volatile Variable
In computer programming, particularly in the C, C++, C#, and Java programming languages, the volatile keyword indicates that a value may change between different accesses, even if it does not appear to be modified. This keyword prevents an optimizing compiler from optimizing away subsequent reads or writes and thus incorrectly reusing a stale value or omitting writes. Volatile values primarily arise in hardware access ( memory-mapped I/O), where reading from or writing to memory is used to communicate with peripheral devices, and in threading, where a different thread may have modified a value. Despite being a common keyword, the behavior of volatile differs significantly between programming languages, and is easily misunderstood. In C and C++, it is a type qualifier, like const, and is a property of the ''type''. Furthermore, in C and C++ it does ''not'' work in most threading scenarios, and that use is discouraged. In Java and C#, it is a property of a variable and ind ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Infinite Loop
In computer programming, an infinite loop (or endless loop) is a sequence of instructions that, as written, will continue endlessly, unless an external intervention occurs ("pull the plug"). It may be intentional. Overview This differs from: * "a type of computer program that runs the same instructions continuously until it is either stopped or interrupted." Consider the following pseudocode: how_many = 0 while is_there_more_data() do how_many = how_many + 1 end display "the number of items counted = " how_many ''The same instructions'' were run ''continuously until it was stopped or interrupted'' . . . by the ''FALSE'' returned at some point by the function ''is_there_more_data''. By contrast, the following loop will not end by itself: birds = 1 fish = 2 while birds + fish > 1 do birds = 3 - birds fish = 3 - fish end ''birds'' will alternate being 1 or 2, while ''fish'' will alternate being 2 or 1. The loop will not stop unless an external intervention occu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Loop-invariant Code Motion
In computer programming, loop-invariant code consists of statements or expressions (in an imperative programming language) that can be moved outside the body of a loop without affecting the semantics of the program. Loop-invariant code motion (also called hoisting or scalar promotion) is a compiler optimization that performs this movement automatically. Example In the following code sample, two optimizations can be applied. int i = 0; while (i < n) Although the calculation x = y + z and x * x is loop-invariant, precautions must be taken before moving the code outside the loop. It is possible that the loop condition is false (for example, if n holds a negative value), and in such case, the loop body should not be executed at all. One way of guaranteeing correct behaviour is using a conditional branch outside of the loop. Evaluating the loop condition can have [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |