|
Dehn Twist
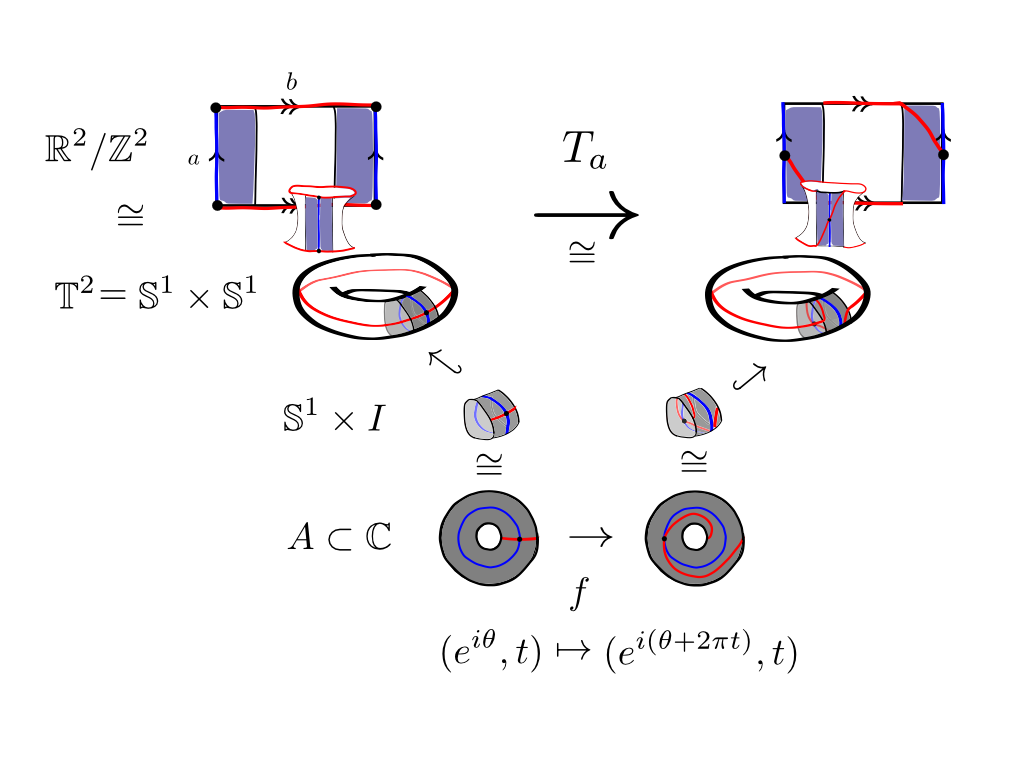
In geometric topology, a branch of mathematics, a Dehn twist is a certain type of self-homeomorphism of a surface (two-dimensional manifold). Definition Suppose that ''c'' is a simple closed curve in a closed, orientable surface ''S''. Let ''A'' be a tubular neighborhood of ''c''. Then ''A'' is an annulus, homeomorphic to the Cartesian product of a circle and a unit interval ''I'': :c \subset A \cong S^1 \times I. Give ''A'' coordinates (''s'', ''t'') where ''s'' is a complex number of the form e^ with \theta \in , 2\pi and . Let ''f'' be the map from ''S'' to itself which is the identity outside of ''A'' and inside ''A'' we have :f(s, t) = \left(se^, t\right). Then ''f'' is a Dehn twist about the curve ''c''. Dehn twists can also be defined on a non-orientable surface ''S'', provided one starts with a 2-sided simple closed curve ''c'' on ''S''. Example Consider the torus represented by a fundamental polygon with edges ''a'' and ''b'' :\mathbb^2 \cong \mat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dehn Twist
In geometric topology, a branch of mathematics, a Dehn twist is a certain type of self-homeomorphism of a surface (two-dimensional manifold). Definition Suppose that ''c'' is a simple closed curve in a closed, orientable surface ''S''. Let ''A'' be a tubular neighborhood of ''c''. Then ''A'' is an annulus, homeomorphic to the Cartesian product of a circle and a unit interval ''I'': :c \subset A \cong S^1 \times I. Give ''A'' coordinates (''s'', ''t'') where ''s'' is a complex number of the form e^ with \theta \in , 2\pi and . Let ''f'' be the map from ''S'' to itself which is the identity outside of ''A'' and inside ''A'' we have :f(s, t) = \left(se^, t\right). Then ''f'' is a Dehn twist about the curve ''c''. Dehn twists can also be defined on a non-orientable surface ''S'', provided one starts with a 2-sided simple closed curve ''c'' on ''S''. Example Consider the torus represented by a fundamental polygon with edges ''a'' and ''b'' :\mathbb^2 \cong \mat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Torus
In geometry, a torus (plural tori, colloquially donut or doughnut) is a surface of revolution generated by revolving a circle in three-dimensional space about an axis that is coplanar with the circle. If the axis of revolution does not touch the circle, the surface has a ring shape and is called a torus of revolution. If the axis of revolution is tangent to the circle, the surface is a horn torus. If the axis of revolution passes twice through the circle, the surface is a spindle torus. If the axis of revolution passes through the center of the circle, the surface is a degenerate torus, a double-covered sphere. If the revolved curve is not a circle, the surface is called a ''toroid'', as in a square toroid. Real-world objects that approximate a torus of revolution include swim rings, inner tubes and ringette rings. Eyeglass lenses that combine spherical and cylindrical correction are toric lenses. A torus should not be confused with a '' solid torus'', which is formed by r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Andrew J
Andrew is the English form of a given name common in many countries. In the 1990s, it was among the top ten most popular names given to boys in English-speaking countries. "Andrew" is frequently shortened to "Andy" or "Drew". The word is derived from the el, Ἀνδρέας, ''Andreas'', itself related to grc, ἀνήρ/ἀνδρός ''aner/andros'', "man" (as opposed to "woman"), thus meaning "manly" and, as consequence, "brave", "strong", "courageous", and "warrior". In the King James Bible, the Greek "Ἀνδρέας" is translated as Andrew. Popularity Australia In 2000, the name Andrew was the second most popular name in Australia. In 1999, it was the 19th most common name, while in 1940, it was the 31st most common name. Andrew was the first most popular name given to boys in the Northern Territory in 2003 to 2015 and continuing. In Victoria, Andrew was the first most popular name for a boy in the 1970s. Canada Andrew was the 20th most popular name chosen for mal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lantern Relation
In geometric topology, a branch of mathematics, the lantern relation is a relation that appears between certain Dehn twists in the mapping class group of a surface. The most general version of the relation involves seven Dehn twists. The relation was discovered by Dennis Johnson in 1979. General form The general form of the lantern relation involves seven Dehn twists in the mapping class group of a disk with three holes, as shown in the figure on the right. According to the relation, : where , , and are the right-handed Dehn twists around the blue curves , , and , and , , , are the right-handed Dehn twists around the four red curves. Note that the Dehn twists , , , on the right-hand side all commute (since the curves are disjoint, so the order in which they appear does not matter. However, the cyclic order of the three Dehn twists on the left does matter: : Also, note that the equalities written above are actually equality up to homotopy In topology, a branch of ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Y-homeomorphism
In mathematics, the y-homeomorphism, or crosscap slide, is a special type of auto-homeomorphism in non-orientable surfaces. It can be constructed by sliding a Möbius band included on the surface around an essential 1-sided closed curve until the original position; thus it is necessary that the surfaces have genus greater than one. The projective plane ^2 has no y-homeomorphism. See also * Lickorish-Wallace theorem References *J. S. Birman, D. R. J. Chillingworth, ''On the homeotopy group of a non-orientable surface'', Trans. Amer. Math. Soc. 247 (1979), 87-124. *D. R. J. Chillingworth, ''A finite set of generators for the homeotopy group of a non-orientable surface'', Proc. Camb. Phil. Soc. 65 (1969), 409–430. *M. Korkmaz, ''Mapping class group of non-orientable surface'', Geometriae Dedicata 89 (2002), 109–133. *W. B. R. Lickorish William Bernard Raymond Lickorish (born 19 February 1938) is a mathematician. He is emeritus professor of geometric topology in the Depa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stephen P
Stephen or Steven is a common English first name. It is particularly significant to Christians, as it belonged to Saint Stephen ( grc-gre, Στέφανος ), an early disciple and deacon who, according to the Book of Acts, was stoned to death; he is widely regarded as the first martyr (or "protomartyr") of the Christian Church. In English, Stephen is most commonly pronounced as ' (). The name, in both the forms Stephen and Steven, is often shortened to Steve or Stevie. The spelling as Stephen can also be pronounced which is from the Greek original version, Stephanos. In English, the female version of the name is Stephanie. Many surnames are derived from the first name, including Stephens, Stevens, Stephenson, and Stevenson, all of which mean "Stephen's (son)". In modern times the name has sometimes been given with intentionally non-standard spelling, such as Stevan or Stevon. A common variant of the name used in English is Stephan ; related names that have found some curr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Genus (mathematics)
In mathematics, genus (plural genera) has a few different, but closely related, meanings. Intuitively, the genus is the number of "holes" of a surface. A sphere has genus 0, while a torus has genus 1. Topology Orientable surfaces The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It is equal to the number of handles on it. Alternatively, it can be defined in terms of the Euler characteristic ''χ'', via the relationship ''χ'' = 2 − 2''g'' for closed surfaces, where ''g'' is the genus. For surfaces with ''b'' boundary components, the equation reads ''χ'' = 2 − 2''g'' − ''b''. In layman's terms, it's the number of "holes" an object has ("holes" interpreted in the sense of doughnut holes; a hollow sphere would be considered as having zero holes in this sense). A torus has 1 such h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homotopy
In topology, a branch of mathematics, two continuous functions from one topological space to another are called homotopic (from grc, ὁμός "same, similar" and "place") if one can be "continuously deformed" into the other, such a deformation being called a homotopy (, ; , ) between the two functions. A notable use of homotopy is the definition of homotopy groups and cohomotopy groups, important invariants in algebraic topology. In practice, there are technical difficulties in using homotopies with certain spaces. Algebraic topologists work with compactly generated spaces, CW complexes, or spectra. Formal definition Formally, a homotopy between two continuous functions ''f'' and ''g'' from a topological space ''X'' to a topological space ''Y'' is defined to be a continuous function H: X \times ,1\to Y from the product of the space ''X'' with the unit interval , 1to ''Y'' such that H(x,0) = f(x) and H(x,1) = g(x) for all x \in X. If we think of the second ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mapping Class Group Of A Surface
In mathematics, and more precisely in topology, the mapping class group of a surface, sometimes called the modular group or Teichmüller modular group, is the group of homeomorphisms of the surface viewed up to continuous (in the compact-open topology) deformation. It is of fundamental importance for the study of 3-manifolds via their embedded surfaces and is also studied in algebraic geometry in relation to moduli problems for curves. The mapping class group can be defined for arbitrary manifolds (indeed, for arbitrary topological spaces) but the 2-dimensional setting is the most studied in group theory. The mapping class group of surfaces are related to various other groups, in particular braid groups and outer automorphism groups. History The mapping class group appeared in the first half of the twentieth century. Its origins lie in the study of the topology of hyperbolic surfaces, and especially in the study of the intersections of closed curves on these surfaces. The earl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Max Dehn
Max Wilhelm Dehn (November 13, 1878 – June 27, 1952) was a German mathematician most famous for his work in geometry, topology and geometric group theory. Born to a Jewish family in Germany, Dehn's early life and career took place in Germany. However, he was forced to retire in 1935 and eventually fled Germany in 1939 and emigrated to the United States. Dehn was a student of David Hilbert, and in his habilitation in 1900 Dehn resolved Hilbert's third problem, making him the first to resolve one of Hilbert's well-known 23 problems. Dehn's students include Ott-Heinrich Keller, Ruth Moufang, Wilhelm Magnus, and the artists Dorothea Rockburne and Ruth Asawa. Biography Dehn was born to a family of Jewish origin in Hamburg, Imperial Germany. He studied the foundations of geometry with Hilbert at Göttingen in 1899, and obtained a proof of the Jordan curve theorem for polygons. In 1900 he wrote his dissertation on the role of the Legendre angle sum theorem in axiomatic geome ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lickorish Twist Theorem
In geometric topology, a branch of mathematics, a Dehn twist is a certain type of self-homeomorphism of a surface (two-dimensional manifold). Definition Suppose that ''c'' is a simple closed curve in a closed, orientable surface ''S''. Let ''A'' be a tubular neighborhood of ''c''. Then ''A'' is an annulus, homeomorphic to the Cartesian product of a circle and a unit interval ''I'': :c \subset A \cong S^1 \times I. Give ''A'' coordinates (''s'', ''t'') where ''s'' is a complex number of the form e^ with \theta \in , 2\pi and . Let ''f'' be the map from ''S'' to itself which is the identity outside of ''A'' and inside ''A'' we have :f(s, t) = \left(se^, t\right). Then ''f'' is a Dehn twist about the curve ''c''. Dehn twists can also be defined on a non-orientable surface ''S'', provided one starts with a 2-sided simple closed curve ''c'' on ''S''. Example Consider the torus represented by a fundamental polygon with edges ''a'' and ''b'' :\mathbb^2 \cong \mathb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homotopy Classes
In topology, a branch of mathematics, two continuous functions from one topological space to another are called homotopic (from grc, ὁμός "same, similar" and "place") if one can be "continuously deformed" into the other, such a deformation being called a homotopy (, ; , ) between the two functions. A notable use of homotopy is the definition of homotopy groups and cohomotopy groups, important invariants in algebraic topology. In practice, there are technical difficulties in using homotopies with certain spaces. Algebraic topologists work with compactly generated spaces, CW complexes, or spectra. Formal definition Formally, a homotopy between two continuous functions ''f'' and ''g'' from a topological space ''X'' to a topological space ''Y'' is defined to be a continuous function H: X \times ,1\to Y from the product of the space ''X'' with the unit interval , 1to ''Y'' such that H(x,0) = f(x) and H(x,1) = g(x) for all x \in X. If we think of the seco ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |