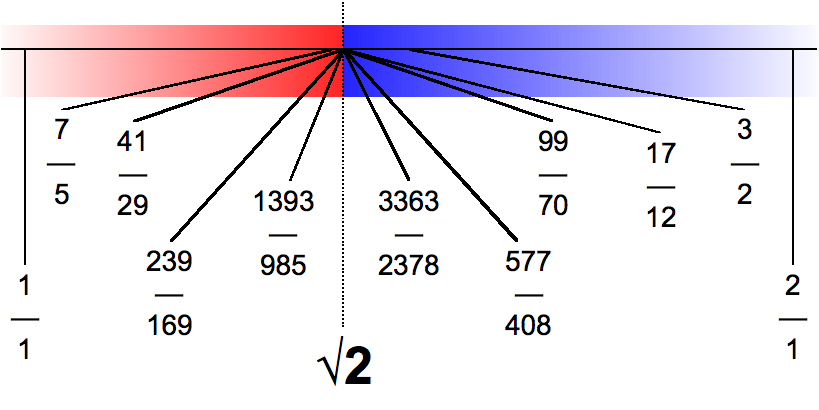
|
Definable Real Number
Informally, a definable real number is a real number that can be uniquely specified by its description. The description may be expressed as a construction or as a formula of a formal language. For example, the positive square root of 2, \sqrt, can be defined as the unique positive solution to the equation x^2 = 2, and it can be constructed with a compass and straightedge. Different choices of a formal language or its interpretation give rise to different notions of definability. Specific varieties of definable numbers include the constructible numbers of geometry, the algebraic numbers, and the computable numbers. Because formal languages can have only countably many formulas, every notion of definable numbers has at most countably many definable real numbers. However, by Cantor's diagonal argument, there are uncountably many real numbers, so almost every real number is undefinable. Constructible numbers One way of specifying a real number uses geometric techniques. A real ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square Root Of 2 Triangle
In Euclidean geometry, a square is a regular polygon, regular quadrilateral, which means that it has four equal sides and four equal angles (90-degree (angle), degree angles, π/2 radian angles, or right angles). It can also be defined as a rectangle with two equal-length adjacent sides. It is the only regular polygon whose Internal and external angle, internal angle, central angle#Central angle of a regular polygon, central angle, and Internal and external angle, external angle are all equal (90°), and whose diagonals are all equal in length. A square with Vertex (geometry), vertices ''ABCD'' would be denoted . Characterizations A Convex polygon, convex quadrilateral is a square if and only if it is any one of the following: * A rectangle with two adjacent equal sides * A rhombus with a right vertex angle * A rhombus with all angles equal * A parallelogram with one right vertex angle and two adjacent equal sides * A quadrilateral with four equal sides and four right angles * A ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Georg Cantor's First Set Theory Article
Cantor's first set theory article contains Georg Cantor's first theorems of transfinite set theory, which studies infinite sets and their properties. One of these theorems is his "revolutionary discovery" that the set of all real numbers is uncountably, rather than countably, infinite. This theorem is proved using Cantor's first uncountability proof, which differs from the more familiar proof using his diagonal argument. The title of the article, "On a Property of the Collection of All Real Algebraic Numbers" ("Ueber eine Eigenschaft des Inbegriffes aller reellen algebraischen Zahlen"), refers to its first theorem: the set of real algebraic numbers is countable. Cantor's article was published in 1874. In 1879, he modified his uncountability proof by using the topological notion of a set being dense in an interval. Cantor's article also contains a proof of the existence of transcendental numbers. Both constructive and non-constructive proofs have been presented as "Cantor's proof. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Analytical Hierarchy
In mathematical logic and descriptive set theory, the analytical hierarchy is an extension of the arithmetical hierarchy. The analytical hierarchy of formulas includes formulas in the language of second-order arithmetic, which can have quantifiers over both the set of natural numbers, \mathbb, and over functions from \mathbb to \mathbb. The analytical hierarchy of sets classifies sets by the formulas that can be used to define them; it is the lightface version of the projective hierarchy. The analytical hierarchy of formulas The notation \Sigma^1_0 = \Pi^1_0 = \Delta^1_0 indicates the class of formulas in the language of second-order arithmetic with number quantifiers but no set quantifiers. This language does not contain set parameters. The Greek letters here are lightface symbols, which indicate this choice of language. Each corresponding boldface symbol denotes the corresponding class of formulas in the extended language with a parameter for each real; see projective hierarch ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Second-order Arithmetic
In mathematical logic, second-order arithmetic is a collection of axiomatic systems that formalize the natural numbers and their subsets. It is an alternative to axiomatic set theory as a foundation for much, but not all, of mathematics. A precursor to second-order arithmetic that involves third-order parameters was introduced by David Hilbert and Paul Bernays in their book ''Grundlagen der Mathematik''. The standard axiomatization of second-order arithmetic is denoted by Z2. Second-order arithmetic includes, but is significantly stronger than, its first-order counterpart Peano arithmetic. Unlike Peano arithmetic, second-order arithmetic allows quantification over sets of natural numbers as well as numbers themselves. Because real numbers can be represented as (infinite) sets of natural numbers in well-known ways, and because second-order arithmetic allows quantification over such sets, it is possible to formalize the real numbers in second-order arithmetic. For this reason, secon ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Predicate (logic)
In logic, a predicate is a symbol which represents a property or a relation. For instance, in the first order formula P(a), the symbol P is a predicate which applies to the individual constant a. Similarly, in the formula R(a,b), R is a predicate which applies to the individual constants a and b. In the semantics of logic, predicates are interpreted as relations. For instance, in a standard semantics for first-order logic, the formula R(a,b) would be true on an interpretation if the entities denoted by a and b stand in the relation denoted by R. Since predicates are non-logical symbols, they can denote different relations depending on the interpretation used to interpret them. While first-order logic only includes predicates which apply to individual constants, other logics may allow predicates which apply to other predicates. Predicates in different systems * In propositional logic, atomic formulas are sometimes regarded as zero-place predicates In a sense, these are nullar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dedekind Cut
In mathematics, Dedekind cuts, named after German mathematician Richard Dedekind but previously considered by Joseph Bertrand, are а method of construction of the real numbers from the rational numbers. A Dedekind cut is a partition of the rational numbers into two sets ''A'' and ''B'', such that all elements of ''A'' are less than all elements of ''B'', and ''A'' contains no greatest element. The set ''B'' may or may not have a smallest element among the rationals. If ''B'' has a smallest element among the rationals, the cut corresponds to that rational. Otherwise, that cut defines a unique irrational number which, loosely speaking, fills the "gap" between ''A'' and ''B''. In other words, ''A'' contains every rational number less than the cut, and ''B'' contains every rational number greater than or equal to the cut. An irrational cut is equated to an irrational number which is in neither set. Every real number, rational or not, is equated to one and only one cut of rati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arithmetical Hierarchy
In mathematical logic, the arithmetical hierarchy, arithmetic hierarchy or Kleene–Mostowski hierarchy (after mathematicians Stephen Cole Kleene and Andrzej Mostowski) classifies certain sets based on the complexity of formulas that define them. Any set that receives a classification is called arithmetical. The arithmetical hierarchy is important in recursion theory, effective descriptive set theory, and the study of formal theories such as Peano arithmetic. The Tarski–Kuratowski algorithm provides an easy way to get an upper bound on the classifications assigned to a formula and the set it defines. The hyperarithmetical hierarchy and the analytical hierarchy extend the arithmetical hierarchy to classify additional formulas and sets. The arithmetical hierarchy of formulas The arithmetical hierarchy assigns classifications to the formulas in the language of first-order arithmetic. The classifications are denoted \Sigma^0_n and \Pi^0_n for natural numbers ''n'' (inclu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Natural Number
In mathematics, the natural numbers are those numbers used for counting (as in "there are ''six'' coins on the table") and ordering (as in "this is the ''third'' largest city in the country"). Numbers used for counting are called ''Cardinal number, cardinal numbers'', and numbers used for ordering are called ''Ordinal number, ordinal numbers''. Natural numbers are sometimes used as labels, known as ''nominal numbers'', having none of the properties of numbers in a mathematical sense (e.g. sports Number (sports), jersey numbers). Some definitions, including the standard ISO/IEC 80000, ISO 80000-2, begin the natural numbers with , corresponding to the non-negative integers , whereas others start with , corresponding to the positive integers Texts that exclude zero from the natural numbers sometimes refer to the natural numbers together with zero as the whole numbers, while in other writings, that term is used instead for the integers (including negative integers). The natural ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Peano Arithmetic
In mathematical logic, the Peano axioms, also known as the Dedekind–Peano axioms or the Peano postulates, are axioms for the natural numbers presented by the 19th century Italian mathematician Giuseppe Peano. These axioms have been used nearly unchanged in a number of metamathematical investigations, including research into fundamental questions of whether number theory is consistent and complete. The need to formalize arithmetic was not well appreciated until the work of Hermann Grassmann, who showed in the 1860s that many facts in arithmetic could be derived from more basic facts about the successor operation and induction. In 1881, Charles Sanders Peirce provided an axiomatization of natural-number arithmetic. In 1888, Richard Dedekind proposed another axiomatization of natural-number arithmetic, and in 1889, Peano published a simplified version of them as a collection of axioms in his book, ''The principles of arithmetic presented by a new method'' ( la, Arithmetice ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chaitin's Constant
In the computer science subfield of algorithmic information theory, a Chaitin constant (Chaitin omega number) or halting probability is a real number that, informally speaking, represents the probability that a randomly constructed program will halt. These numbers are formed from a construction due to Gregory Chaitin. Although there are infinitely many halting probabilities, one for each method of encoding programs, it is common to use the letter Ω to refer to them as if there were only one. Because Ω depends on the program encoding used, it is sometimes called Chaitin's construction when not referring to any specific encoding. Each halting probability is a normal and transcendental real number that is not computable, which means that there is no algorithm to compute its digits. Each halting probability is Martin-Löf random, meaning there is not even any algorithm which can reliably guess its digits. Background The definition of a halting probability relies on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algorithmically Random Sequence
Intuitively, an algorithmically random sequence (or random sequence) is a sequence of binary digits that appears random to any algorithm running on a (prefix-free or not) universal Turing machine. The notion can be applied analogously to sequences on any finite alphabet (e.g. decimal digits). Random sequences are key objects of study in algorithmic information theory. As different types of algorithms are sometimes considered, ranging from algorithms with specific bounds on their running time to algorithms which may ask questions of an oracle machine, there are different notions of randomness. The most common of these is known as Martin-Löf randomness (K-randomness or 1-randomness), but stronger and weaker forms of randomness also exist. When the term "algorithmically random" is used to refer to a particular single (finite or infinite) sequence without clarification, it is usually taken to mean "incompressible" or, in the case the sequence is infinite and prefix algorithmically r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Specker Sequence
In computability theory, a Specker sequence is a computable, monotonically increasing, bounded sequence of rational numbers whose supremum is not a computable real number. The first example of such a sequence was constructed by Ernst Specker (1949). The existence of Specker sequences has consequences for computable analysis. The fact that such sequences exist means that the collection of all computable real numbers does not satisfy the least upper bound principle of real analysis, even when considering only computable sequences. A common way to resolve this difficulty is to consider only sequences that are accompanied by a modulus of convergence; no Specker sequence has a computable modulus of convergence. More generally, a Specker sequence is called a ''recursive counterexample'' to the least upper bound principle, i.e. a construction that shows that this theorem is false when restricted to computable reals. The least upper bound principle has also been analyzed in the progr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
