|
Decisional Diffie–Hellman Assumption
The decisional Diffie–Hellman (DDH) assumption is a computational hardness assumption about a certain problem involving discrete logarithms in cyclic groups. It is used as the basis to prove the security of many cryptographic protocols, most notably the ElGamal and Cramer–Shoup cryptosystems. Definition Consider a (multiplicative) cyclic group G of order q, and with generator g. The DDH assumption states that, given g^a and g^b for uniformly and independently chosen a,b \in \mathbb_q, the value g^ "looks like" a random element in G. This intuitive notion can be formally stated by saying that the following two probability distributions are computationally indistinguishable (in the security parameter, n=\log(q)): * (g^a,g^b,g^), where a and b are randomly and independently chosen from \mathbb_q. * (g^a,g^b,g^c), where a,b,c are randomly and independently chosen from \mathbb_q. Triples of the first kind are often called DDH triplet or DDH tuples. Relation to other assumptio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computational Hardness Assumption
In computational complexity theory, a computational hardness assumption is the hypothesis that a particular problem cannot be solved efficiently (where ''efficiently'' typically means "in polynomial time"). It is not known how to prove (unconditional) hardness for essentially any useful problem. Instead, computer scientists rely on reductions to formally relate the hardness of a new or complicated problem to a computational hardness assumption about a problem that is better-understood. Computational hardness assumptions are of particular importance in cryptography. A major goal in cryptography is to create cryptographic primitives with provable security. In some cases, cryptographic protocols are found to have information theoretic security; the one-time pad is a common example. However, information theoretic security cannot always be achieved; in such cases, cryptographers fall back to computational security. Roughly speaking, this means that these systems are secure ''assumin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isomorphism
In mathematics, an isomorphism is a structure-preserving mapping or morphism between two structures of the same type that can be reversed by an inverse mapping. Two mathematical structures are isomorphic if an isomorphism exists between them. The word is derived . The interest in isomorphisms lies in the fact that two isomorphic objects have the same properties (excluding further information such as additional structure or names of objects). Thus isomorphic structures cannot be distinguished from the point of view of structure only, and may often be identified. In mathematical jargon, one says that two objects are the same up to an isomorphism. A common example where isomorphic structures cannot be identified is when the structures are substructures of a larger one. For example, all subspaces of dimension one of a vector space are isomorphic and cannot be identified. An automorphism is an isomorphism from a structure to itself. An isomorphism between two structures is a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
XDH Assumption
The external Diffie–Hellman (XDH) assumption is a computational hardness assumption used in elliptic curve cryptography. The XDH assumption holds if there exist certain subgroups of elliptic curves which have useful properties for cryptography. Specifically, XDH implies the existence of two distinct groups \langle_1, _2\rangle with the following properties: # The discrete logarithm problem (DLP), the computational Diffie–Hellman problem (CDH), and the computational co-Diffie–Hellman problem are all intractable in _1 and _2. # There exists an efficiently computable bilinear map (pairing) e(\cdot, \cdot) : _1 \times _2 \rightarrow _T. # The decisional Diffie–Hellman problem (DDH) is intractable in _1. The above formulation is referred to as asymmetric XDH. A stronger version of the assumption (symmetric XDH, or SXDH) holds if DDH is ''also'' intractable in _2. The XDH assumption is used in some pairing-based cryptographic protocols. In certain ellip ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computational Hardness Assumptions
In computational complexity theory, a computational hardness assumption is the hypothesis that a particular problem cannot be solved efficiently (where ''efficiently'' typically means "in polynomial time"). It is not known how to prove (unconditional) hardness for essentially any useful problem. Instead, computer scientists rely on reductions to formally relate the hardness of a new or complicated problem to a computational hardness assumption about a problem that is better-understood. Computational hardness assumptions are of particular importance in cryptography. A major goal in cryptography is to create cryptographic primitives with provable security. In some cases, cryptographic protocols are found to have information theoretic security; the one-time pad is a common example. However, information theoretic security cannot always be achieved; in such cases, cryptographers fall back to computational security. Roughly speaking, this means that these systems are secure ''assuming ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
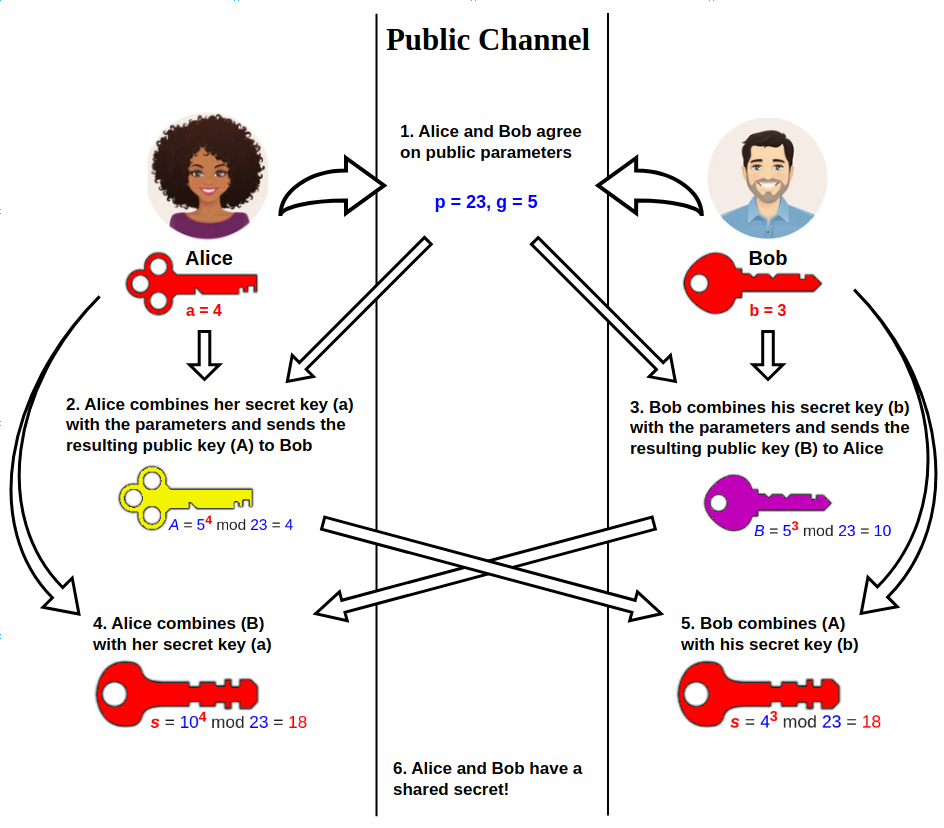
Diffie–Hellman Key Exchange
Diffie–Hellman (DH) key exchangeSynonyms of Diffie–Hellman key exchange include: * Diffie–Hellman–Merkle key exchange * Diffie–Hellman key agreement * Diffie–Hellman key establishment * Diffie–Hellman key negotiation * Exponential key exchange * Diffie–Hellman protocol * Diffie–Hellman handshake is a mathematical method of securely generating a symmetric cryptographic key over a public channel and was one of the first public-key protocols as conceived by Ralph Merkle and named after Whitfield Diffie and Martin Hellman. DH is one of the earliest practical examples of public key exchange implemented within the field of cryptography. Published in 1976 by Diffie and Hellman, this is the earliest publicly known work that proposed the idea of a private key and a corresponding public key. Traditionally, secure encrypted communication between two parties required that they first exchange keys by some secure physical means, such as paper key lists transported by a tr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diffie–Hellman Problem
The Diffie–Hellman problem (DHP) is a mathematical problem first proposed by Whitfield Diffie and Martin Hellman in the context of cryptography and serves as the theoretical basis of the Diffie–Hellman key exchange and its derivatives. The motivation for this problem is that many security systems use one-way functions: mathematical operations that are fast to compute, but hard to reverse. For example, they enable encrypting a message, but reversing the encryption is difficult. If solving the DHP were easy, these systems would be easily broken. Problem description The Diffie–Hellman problem is stated informally as follows: : Given an element g and the values of g^x and g^y, what is the value of g^? Formally, g is a generator of some group (typically the multiplicative group of a finite field or an elliptic curve group) and x and y are randomly chosen integers. For example, in the Diffie–Hellman key exchange, an eavesdropper observes g^ and g^ exchanged as part of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tate Pairing
In mathematics, Tate pairing is any of several closely related bilinear pairings involving elliptic curves or abelian varieties, usually over local or finite fields, based on the Tate duality pairings introduced by and extended by . applied the Tate pairing over finite fields to cryptography. See also * Weil pairing In mathematics, the Weil pairing is a pairing (bilinear form, though with multiplicative notation) on the points of order dividing ''n'' of an elliptic curve ''E'', taking values in ''n''th roots of unity. More generally there is a similar Weil ... References * * * * Pairing-based cryptography Elliptic curve cryptography Elliptic curves {{Crypto-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Weil Pairing
In mathematics, the Weil pairing is a pairing (bilinear form, though with multiplicative notation) on the points of order dividing ''n'' of an elliptic curve ''E'', taking values in ''n''th roots of unity. More generally there is a similar Weil pairing between points of order ''n'' of an abelian variety and its dual. It was introduced by André Weil (1940) for Jacobians of curves, who gave an abstract algebraic definition; the corresponding results for elliptic functions were known, and can be expressed simply by use of the Weierstrass sigma function. Formulation Choose an elliptic curve ''E'' defined over a field ''K'', and an integer ''n'' > 0 (we require ''n'' to be coprime to char(''K'') if char(''K'') > 0) such that ''K'' contains a primitive nth root of unity. Then the ''n''-torsion on E(\overline) is known to be a Cartesian product of two cyclic groups of order ''n''. The Weil pairing produces an ''n''-th root of unity :w(P,Q) \in \mu_n by mea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Supersingular Elliptic Curve
In algebraic geometry, supersingular elliptic curves form a certain class of elliptic curves over a field of characteristic p>0 with unusually large endomorphism rings. Elliptic curves over such fields which are not supersingular are called ''ordinary'' and these two classes of elliptic curves behave fundamentally differently in many aspects. discovered supersingular elliptic curves during his work on the Riemann hypothesis for elliptic curves by observing that positive characteristic elliptic curves could have endomorphism rings of unusually large rank 4, and developed their basic theory. The term "supersingular" has nothing to do with singular points of curves, and all supersingular elliptic curves are non-singular. It comes from the phrase " singular values of the j-invariant" used for values of the -invariant for which a complex elliptic curve has complex multiplication. The complex elliptic curves with complex multiplication are those for which the endomorphism ring has t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Legendre Symbol
In number theory, the Legendre symbol is a multiplicative function with values 1, −1, 0 that is a quadratic character modulo of an odd prime number ''p'': its value at a (nonzero) quadratic residue mod ''p'' is 1 and at a non-quadratic residue (''non-residue'') is −1. Its value at zero is 0. The Legendre symbol was introduced by Adrien-Marie Legendre in 1797 or 1798 in the course of his attempts at proving the law of quadratic reciprocity. Generalizations of the symbol include the Jacobi symbol and Dirichlet characters of higher order. The notational convenience of the Legendre symbol inspired introduction of several other "symbols" used in algebraic number theory, such as the Hilbert symbol and the Artin symbol. Definition Let p be an odd prime number. An integer a is a quadratic residue modulo p if it is modular arithmetic, congruent to a square number, perfect square modulo p and is a quadratic nonresidue modulo p otherwise. The Legendre symbol is a function of a a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jacobian Variety
In mathematics, the Jacobian variety ''J''(''C'') of a non-singular algebraic curve ''C'' of genus ''g'' is the moduli space of degree 0 line bundles. It is the connected component of the identity in the Picard group of ''C'', hence an abelian variety. Introduction The Jacobian variety is named after Carl Gustav Jacobi, who proved the complete version of the Abel–Jacobi theorem, making the injectivity statement of Niels Abel into an isomorphism. It is a principally polarized abelian variety, of dimension ''g'', and hence, over the complex numbers, it is a complex torus. If ''p'' is a point of ''C'', then the curve ''C'' can be mapped to a subvariety of ''J'' with the given point ''p'' mapping to the identity of ''J'', and ''C'' generates ''J'' as a group. Construction for complex curves Over the complex numbers, the Jacobian variety can be realized as the quotient space ''V''/''L'', where ''V'' is the dual of the vector space of all global holomorphic differenti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |