|
Cycle (algebraic Topology)
In algebraic topology, a -chain is a formal linear combination of the -cells in a cell complex. In simplicial complexes (respectively, cubical complexes), -chains are combinations of -simplices (respectively, -cubes), but not necessarily connected. Chains are used in homology; the elements of a homology group are equivalence classes of chains. Definition For a simplicial complex X, the group C_n(X) of n-chains of X is given by: C_n(X) = \left\ where \sigma_i are singular n-simplices of X. Note that any element in C_n(X) not necessary to be a connected simplicial complex. Integration on chains Integration is defined on chains by taking the linear combination of integrals over the simplices in the chain with coefficients (which are typically integers). The set of all ''k''-chains forms a group and the sequence of these groups is called a chain complex. Boundary operator on chains The boundary of a chain is the linear combination of boundaries of the simplices in the chain. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebraic Topology
Algebraic topology is a branch of mathematics that uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariant (mathematics), invariants that classification theorem, classify topological spaces up to homeomorphism, though usually most classify up to Homotopy#Homotopy equivalence and null-homotopy, homotopy equivalence. Although algebraic topology primarily uses algebra to study topological problems, using topology to solve algebraic problems is sometimes also possible. Algebraic topology, for example, allows for a convenient proof that any subgroup of a free group is again a free group. Main branches of algebraic topology Below are some of the main areas studied in algebraic topology: Homotopy groups In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space. Intuitively, homotopy gro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chainline
Chainline is the angle of a bicycle chain relative to the centerline of the bicycle frame. A bicycle is said to have perfect chainline if the chain is parallel to the centerline of the frame, which means that the rear sprocket is directly behind the front chainring. Chainline also refers to the distance between a sprocket and the centerline of the frame. Bicycles without a straight chainline are slightly less efficient due to frictional losses incurred by running the chain at an angle between the front chainring and rear sprocket. This is the main reason that a single-speed bicycle can be more efficient than a derailleur geared bicycle. Single-speed bicycles should have the straightest possible chainline. See also * Bicycle gearing Bicycle gearing is the aspect of a bicycle drivetrain that determines the relation between the cadence, the rate at which the rider pedals, and the rate at which the drive wheel turns. On some bicycles there is only one gear and, therefore, ... ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stokes' Theorem
Stokes's theorem, also known as the Kelvin–Stokes theorem Nagayoshi Iwahori, et al.:"Bi-Bun-Seki-Bun-Gaku" Sho-Ka-Bou(jp) 1983/12Written in Japanese)Atsuo Fujimoto;"Vector-Kai-Seki Gendai su-gaku rekucha zu. C(1)" :ja:培風館, Bai-Fu-Kan(jp)(1979/01) [] (Written in Japanese) after Lord Kelvin and Sir George Stokes, 1st Baronet, George Stokes, the fundamental theorem for curls or simply the curl theorem, is a theorem in vector calculus on . Given a vector field, the theorem relates the integral of the curl of the vector field over some surface, to the line integral of the vector field around the boundary of the surface. The classical Stokes' theorem can be stated in one sentence: The line integral of a vector field over a loop is equal to the ''flux of its curl'' through the enclosed surface. Stokes' theorem is a special case of the generalized Stokes' theorem. In particular, a vector field on can be considered as a 1-form in which case its curl is its exterior derivat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Exterior Derivative
On a differentiable manifold, the exterior derivative extends the concept of the differential of a function to differential forms of higher degree. The exterior derivative was first described in its current form by Élie Cartan in 1899. The resulting calculus, known as exterior calculus, allows for a natural, metric-independent generalization of Stokes' theorem, Gauss's theorem, and Green's theorem from vector calculus. If a differential -form is thought of as measuring the flux through an infinitesimal - parallelotope at each point of the manifold, then its exterior derivative can be thought of as measuring the net flux through the boundary of a -parallelotope at each point. Definition The exterior derivative of a differential form of degree (also differential -form, or just -form for brevity here) is a differential form of degree . If is a smooth function (a -form), then the exterior derivative of is the differential of . That is, is the unique -form such that for e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differential Geometry
Differential geometry is a mathematical discipline that studies the geometry of smooth shapes and smooth spaces, otherwise known as smooth manifolds. It uses the techniques of differential calculus, integral calculus, linear algebra and multilinear algebra. The field has its origins in the study of spherical geometry as far back as antiquity. It also relates to astronomy, the geodesy of the Earth, and later the study of hyperbolic geometry by Lobachevsky. The simplest examples of smooth spaces are the plane and space curves and surfaces in the three-dimensional Euclidean space, and the study of these shapes formed the basis for development of modern differential geometry during the 18th and 19th centuries. Since the late 19th century, differential geometry has grown into a field concerned more generally with geometric structures on differentiable manifolds. A geometric structure is one which defines some notion of size, distance, shape, volume, or other rigidifying structu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homology (mathematics)
In mathematics, homology is a general way of associating a sequence of algebraic objects, such as abelian groups or modules, with other mathematical objects such as topological spaces. Homology groups were originally defined in algebraic topology. Similar constructions are available in a wide variety of other contexts, such as abstract algebra, groups, Lie algebras, Galois theory, and algebraic geometry. The original motivation for defining homology groups was the observation that two shapes can be distinguished by examining their holes. For instance, a circle is not a disk because the circle has a hole through it while the disk is solid, and the ordinary sphere is not a circle because the sphere encloses a two-dimensional hole while the circle encloses a one-dimensional hole. However, because a hole is "not there", it is not immediately obvious how to define a hole or how to distinguish different kinds of holes. Homology was originally a rigorous mathematical method for defi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Telescoping Sum
In mathematics, a telescoping series is a series whose general term t_n can be written as t_n=a_n-a_, i.e. the difference of two consecutive terms of a sequence (a_n). As a consequence the partial sums only consists of two terms of (a_n) after cancellation. The cancellation technique, with part of each term cancelling with part of the next term, is known as the method of differences. For example, the series :\sum_^\infty\frac (the series of reciprocals of pronic numbers) simplifies as :\begin \sum_^\infty \frac & = \sum_^\infty \left( \frac - \frac \right) \\ & = \lim_ \sum_^N \left( \frac - \frac \right) \\ & = \lim_ \left\lbrack \right\rbrack \\ & = \lim_ \left\lbrack \right\rbrack \\ & = \lim_ \left\lbrack \right\rbrack = 1. \end An early statement of the formula for the sum or partial sums of a telescoping series can be found in a 1644 work by Evangelista Torricelli, ''De dimensione parabolae''. In general Telescoping sums are finite sums in which pairs ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
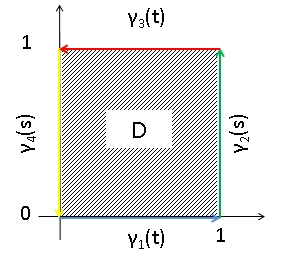
Path (topology)
In mathematics, a path in a topological space X is a continuous function from the closed unit interval , 1/math> into X. Paths play an important role in the fields of topology and mathematical analysis. For example, a topological space for which there exists a path connecting any two points is said to be path-connected. Any space may be broken up into path-connected components. The set of path-connected components of a space X is often denoted \pi_0(X). One can also define paths and loops in pointed spaces, which are important in homotopy theory. If X is a topological space with basepoint x_0, then a path in X is one whose initial point is x_0. Likewise, a loop in X is one that is based at x_0. Definition A ''curve'' in a topological space X is a continuous function f : J \to X from a non-empty and non-degenerate interval J \subseteq \R. A in X is a curve f : , b\to X whose domain , b/math> is a compact non-degenerate interval (meaning a is homeomorphic to , 1 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Closed Polygonal Line
Closed may refer to: Mathematics * Closure (mathematics), a set, along with operations, for which applying those operations on members always results in a member of the set * Closed set, a set which contains all its limit points * Closed interval, an interval which includes its endpoints * Closed line segment, a line segment which includes its endpoints * Closed manifold, a compact manifold which has no boundary Other uses * Closed (poker), a betting round where no player will have the right to raise * ''Closed'' (album), a 2010 album by Bomb Factory * Closed GmbH, a German fashion brand * Closed class, in linguistics, a class of words or other entities which rarely changes See also * * Close (other) * Closed loop (other) * Closing (other) * Closure (other) * Open (other) Open or OPEN may refer to: Music * Open (band), Australian pop/rock band * The Open (band), English indie rock band * ''Open'' (Blues Image album), 1969 * ' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chain Complex
In mathematics, a chain complex is an algebraic structure that consists of a sequence of abelian groups (or module (mathematics), modules) and a sequence of group homomorphism, homomorphisms between consecutive groups such that the image (mathematics), image of each homomorphism is included in the kernel (algebra)#Group homomorphisms, kernel of the next. Associated to a chain complex is its Homology (mathematics), homology, which describes how the images are included in the kernels. A cochain complex is similar to a chain complex, except that its homomorphisms are in the opposite direction. The homology of a cochain complex is called its cohomology. In algebraic topology, the singular chain complex of a topological space X is constructed using continuous function#continuous functions between topological spaces, continuous maps from a simplex to X, and the homomorphisms of the chain complex capture how these maps restrict to the boundary of the simplex. The homology of this chain co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Order Theory
Order theory is a branch of mathematics that investigates the intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and provides basic definitions. A list of order-theoretic terms can be found in the order theory glossary. Background and motivation Orders are everywhere in mathematics and related fields like computer science. The first order often discussed in primary school is the standard order on the natural numbers e.g. "2 is less than 3", "10 is greater than 5", or "Does Tom have fewer cookies than Sally?". This intuitive concept can be extended to orders on other sets of numbers, such as the integers and the reals. The idea of being greater than or less than another number is one of the basic intuitions of number systems (compare with numeral systems) in general (although one usually is also interested in the actual difference ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Singular Homology
In algebraic topology, singular homology refers to the study of a certain set of algebraic invariants of a topological space ''X'', the so-called homology groups H_n(X). Intuitively, singular homology counts, for each dimension ''n'', the ''n''-dimensional holes of a space. Singular homology is a particular example of a homology theory, which has now grown to be a rather broad collection of theories. Of the various theories, it is perhaps one of the simpler ones to understand, being built on fairly concrete constructions (see also the related theory simplicial homology). In brief, singular homology is constructed by taking maps of the standard ''n''-simplex to a topological space, and composing them into formal sums, called singular chains. The boundary operation – mapping each ''n''-dimensional simplex to its (''n''−1)-dimensional boundary – induces the singular chain complex. The singular homology is then the homology of the chain complex. The resulting ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.jpg "Click for more on -> Chainline")
