|
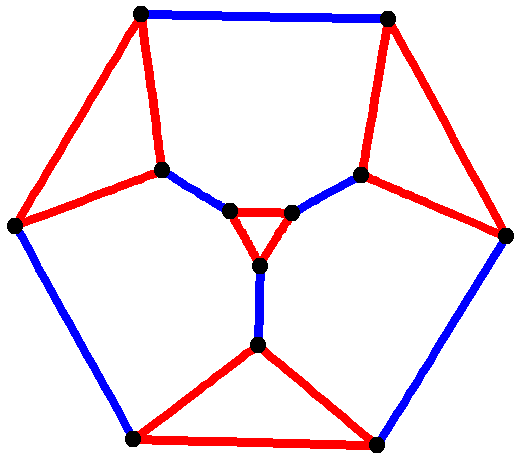
Cube-connected Cycles
In graph theory, the cube-connected cycles is an undirected cubic graph, formed by replacing each vertex of a hypercube graph by a cycle. It was introduced by for use as a network topology in parallel computing. Definition The cube-connected cycles of order ''n'' (denoted CCC''n'') can be defined as a graph formed from a set of ''n''2''n'' nodes, indexed by pairs of numbers (''x'', ''y'') where 0 ≤ ''x'' < 2''n'' and 0 ≤ ''y'' < ''n''. Each such node is connected to three neighbors: , , and , where "⊕" denotes the bitwise exclusive or operation on binary numbers. This graph can also be interpreted as the result of replacing each vertex of an ''n''-dimensional hypercube graph by an ''n''-vertex cycle. The hypercube graph vertices are indexed by the numbers ''x'', and the positions within each cycle by the numbers ''y''. Properties The cube-connected cycles of order ''n'' is the Cayley graph of a group that acts on binary words of length ''n'' by rotation an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Group Action (mathematics)
In mathematics, a group action of a group G on a set (mathematics), set S is a group homomorphism from G to some group (under function composition) of functions from S to itself. It is said that G acts on S. Many sets of transformation (function), transformations form a group (mathematics), group under function composition; for example, the rotation (mathematics), rotations around a point in the plane. It is often useful to consider the group as an abstract group, and to say that one has a group action of the abstract group that consists of performing the transformations of the group of transformations. The reason for distinguishing the group from the transformations is that, generally, a group of transformations of a mathematical structure, structure acts also on various related structures; for example, the above rotation group also acts on triangles by transforming triangles into triangles. If a group acts on a structure, it will usually also act on objects built from that st ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Network Topology
Network topology is the arrangement of the elements (Data link, links, Node (networking), nodes, etc.) of a communication network. Network topology can be used to define or describe the arrangement of various types of telecommunication networks, including command and control radio networks, industrial Fieldbus, fieldbusses and computer networks. Network topology is the topological structure of a network and may be depicted physically or logically. It is an application of graph theory wherein communicating devices are modeled as nodes and the connections between the devices are modeled as links or lines between the nodes. Physical topology is the placement of the various components of a network (e.g., device location and cable installation), while logical topology illustrates how data flows within a network. Distances between nodes, physical interconnections, transmission rates, or signal types may differ between two different networks, yet their logical topologies may be identica ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Computer Networking
A computer network is a collection of communicating computers and other devices, such as printers and smart phones. In order to communicate, the computers and devices must be connected by wired media like copper cables, optical fibers, or by wireless communication. The devices may be connected in a variety of network topologies. In order to communicate over the network, computers use agreed-on rules, called communication protocols, over whatever medium is used. The computer network can include personal computers, Server (computing), servers, networking hardware, or other specialized or general-purpose Host (network), hosts. They are identified by network addresses and may have hostnames. Hostnames serve as memorable labels for the nodes and are rarely changed after initial assignment. Network addresses serve for locating and identifying the nodes by communication protocols such as the Internet Protocol. Computer networks may be classified by many criteria, including the tr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Pancyclic Graph
In the mathematical study of graph theory, a pancyclic graph is a directed graph or undirected graph that contains cycles of all possible lengths from three up to the number of vertices in the graph.. Pancyclic graphs are a generalization of Hamiltonian graphs, graphs which have a cycle of the maximum possible length. Definitions An n-vertex graph G is pancyclic if, for every k in the range 3 \leq k \leq n, it contains a cycle of length k. It is node-pancyclic or vertex-pancyclic if, for every vertex v and every k in the same range, it contains a cycle of length k that contains v.. Similarly, it is edge-pancyclic if, for every edge e and every k in the same range, it contains a cycle of length k that contains e. A bipartite graph cannot be pancyclic, because it does not contain any odd-length cycles, but it is said to be bipancyclic if it contains cycles of all even lengths from 4 to n. Planar graphs A maximal outerplanar graph is a graph formed by a simple polygon in the pl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Hamiltonian Cycle
In the mathematics, mathematical field of graph theory, a Hamiltonian path (or traceable path) is a path (graph theory), path in an undirected or directed graph that visits each vertex (graph theory), vertex exactly once. A Hamiltonian cycle (or Hamiltonian circuit) is a cycle (graph theory), cycle that visits each vertex exactly once. A Hamiltonian path that starts and ends at adjacent vertices can be completed by adding one more edge to form a Hamiltonian cycle, and removing any edge from a Hamiltonian cycle produces a Hamiltonian path. The computational problems of determining whether such paths and cycles exist in graphs are NP-complete; see Hamiltonian path problem for details. Hamiltonian paths and cycles are named after William Rowan Hamilton, who invented the icosian game, now also known as ''Hamilton's puzzle'', which involves finding a Hamiltonian cycle in the edge graph of the dodecahedron. Hamilton solved this problem using the icosian calculus, an algebraic structur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Lovász Conjecture
In graph theory, the Lovász conjecture (1969) is a classical problem on Hamiltonian paths in graphs. It says: : Every finite connected vertex-transitive graph contains a Hamiltonian path. Originally László Lovász stated the problem in the opposite way, but this version became standard. In 1996, László Babai published a conjecture sharply contradicting this conjecture, but both conjectures remain widely open. It is not even known if a single counterexample would necessarily lead to a series of counterexamples. Historical remarks The problem of finding Hamiltonian paths in highly symmetric graphs is quite old. As Donald Knuth describes it in volume 4 of ''The Art of Computer Programming'', the problem originated in British campanology (bell-ringing). Such Hamiltonian paths and cycles are also closely connected to Gray codes. In each case the constructions are explicit. Variants of the Lovász conjecture Hamiltonian cycle Another version of Lovász conjecture states tha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Crossing Number (graph Theory)
In graph theory, the crossing number of a Graph (discrete mathematics), graph is the lowest number of edge crossings of a plane graph drawing, drawing of the graph . For instance, a graph is planar graph, planar if and only if its crossing number is zero. Determining the crossing number continues to be of great importance in graph drawing, as user studies have shown that drawing graphs with few crossings makes it easier for people to understand the drawing. The study of crossing numbers originated in Turán's brick factory problem, in which Pál Turán asked for a factory plan that minimized the number of crossings between tracks connecting brick kilns to storage sites. Mathematically, this problem can be formalized as asking for the crossing number of a complete bipartite graph. The same problem arose independently in sociology at approximately the same time, in connection with the construction of sociograms. Turán's conjectured formula for the crossing numbers of complete bip ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Diameter
In geometry, a diameter of a circle is any straight line segment that passes through the centre of the circle and whose endpoints lie on the circle. It can also be defined as the longest Chord (geometry), chord of the circle. Both definitions are also valid for the diameter of a sphere. In more modern usage, the length d of a diameter is also called the diameter. In this sense one speaks of diameter rather than diameter (which refers to the line segment itself), because all diameters of a circle or sphere have the same length, this being twice the radius r. :d = 2r \qquad\text\qquad r = \frac. The word "diameter" is derived from (), "diameter of a circle", from (), "across, through" and (), "measure". It is often abbreviated \text, \text, d, or \varnothing. Constructions With straightedge and compass, a diameter of a given circle can be constructed as the perpendicular bisector of an arbitrary chord. Drawing two diameters in this way can be used to locate the center of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Vertex-transitive Graph
In the mathematics, mathematical field of graph theory, an Graph automorphism, automorphism is a permutation of the Vertex (graph theory), vertices such that edges are mapped to edges and non-edges are mapped to non-edges. A graph is a vertex-transitive graph if, given any two vertices and of , there is an automorphism such that :f(v_1) = v_2.\ In other words, a graph is vertex-transitive if its automorphism group Group action (mathematics), acts Group_action#Remarkable properties of actions, transitively on its vertices.. A graph is vertex-transitive if and only if its graph complement is, since the group actions are identical. Every symmetric graph without isolated vertex, isolated vertices is vertex-transitive, and every vertex-transitive graph is Regular graph, regular. However, not all vertex-transitive graphs are symmetric (for example, the edges of the truncated tetrahedron), and not all regular graphs are vertex-transitive (for example, the Frucht graph and Tietze's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Circular Shift
In combinatorial mathematics, a circular shift is the operation of rearranging the entries in a tuple, either by moving the final entry to the first position, while shifting all other entries to the next position, or by performing the inverse operation. A circular shift is a special kind of cyclic permutation, which in turn is a special kind of permutation. Formally, a circular shift is a permutation σ of the ''n'' entries in the tuple such that either :\sigma(i)\equiv (i+1) modulo ''n'', for all entries ''i'' = 1, ..., ''n'' or :\sigma(i)\equiv (i-1) modulo ''n'', for all entries ''i'' = 1, ..., ''n''. The result of repeatedly applying circular shifts to a given tuple are also called the circular shifts of the tuple. For example, repeatedly applying circular shifts to the four-tuple (''a'', ''b'', ''c'', ''d'') successively gives * (''d'', ''a'', ''b'', ''c''), * (''c'', ''d'', ''a'', ''b''), * (''b'', ''c'', ''d'', ''a''), * (''a'', ''b'', ''c'', ''d'') (the original four-tup ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Group (mathematics)
In mathematics, a group is a Set (mathematics), set with an Binary operation, operation that combines any two elements of the set to produce a third element within the same set and the following conditions must hold: the operation is Associative property, associative, it has an identity element, and every element of the set has an inverse element. For example, the integers with the addition, addition operation form a group. The concept of a group was elaborated for handling, in a unified way, many mathematical structures such as numbers, geometric shapes and polynomial roots. Because the concept of groups is ubiquitous in numerous areas both within and outside mathematics, some authors consider it as a central organizing principle of contemporary mathematics. In geometry, groups arise naturally in the study of symmetries and geometric transformations: The symmetries of an object form a group, called the symmetry group of the object, and the transformations of a given type form a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |