|
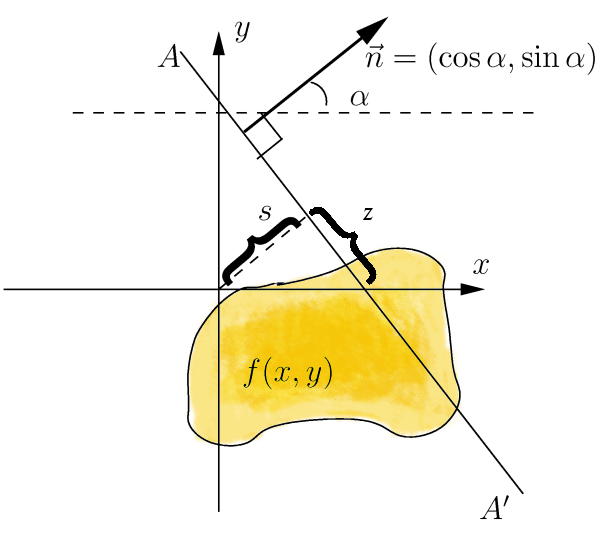
Crofton Formula
In mathematics, the Crofton formula, named after Morgan Crofton (1826–1915), is a classic result of integral geometry relating the length of a curve to the expected number of times a "random" line intersects it. Statement Suppose \gamma is a rectifiable plane curve. Given an oriented line ''ℓ'', let n_\gamma(''ℓ'') be the number of points at which \gamma and ''ℓ'' intersect. We can parametrize the general line ''ℓ'' by the direction \varphi in which it points and its signed distance p from the origin. The Crofton formula expresses the arc length of the curve \gamma in terms of an integral over the space of all oriented lines: :\operatorname (\gamma) = \frac14\iint n_\gamma(\varphi, p)\; d\varphi\; dp. The differential form :d\varphi\wedge dp is invariant under rigid motions of \R^2, so it is a natural integration measure for speaking of an "average" number of intersections. It is usually called the kinematic measure. The right-hand side in the Crofton formula is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Almost Everywhere
In measure theory (a branch of mathematical analysis), a property holds almost everywhere if, in a technical sense, the set for which the property holds takes up nearly all possibilities. The notion of "almost everywhere" is a companion notion to the concept of measure zero, and is analogous to the notion of ''almost surely'' in probability theory. More specifically, a property holds almost everywhere if it holds for all elements in a set except a subset of measure zero, or equivalently, if the set of elements for which the property holds is conull. In cases where the measure is not complete, it is sufficient that the set be contained within a set of measure zero. When discussing sets of real numbers, the Lebesgue measure is usually assumed unless otherwise stated. The term ''almost everywhere'' is abbreviated ''a.e.''; in older literature ''p.p.'' is used, to stand for the equivalent French language phrase ''presque partout''. A set with full measure is one whose complement i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integral Geometry
In mathematics, integral geometry is the theory of measures on a geometrical space invariant under the symmetry group of that space. In more recent times, the meaning has been broadened to include a view of invariant (or equivariant) transformations from the space of functions on one geometrical space to the space of functions on another geometrical space. Such transformations often take the form of integral transforms such as the Radon transform and its generalizations. Classical context Integral geometry as such first emerged as an attempt to refine certain statements of geometric probability theory. The early work of Luis Santaló and Wilhelm Blaschke was in this connection. It follows from the classic theorem of Crofton expressing the length of a plane curve as an expectation of the number of intersections with a random line. Here the word 'random' must be interpreted as subject to correct symmetry considerations. There is a sample space of lines, one on which the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Steinhaus Longimeter
The Steinhaus longimeter, patented by the professor Hugo Steinhaus, is an instrument used to measure the lengths of curves on maps. Description It is a transparent sheet of three grids, turned against each other by 30 degrees, each consisting of parallel lines spaced at equal distances 3.82 mm. The measurement is done by counting crossings of the curve with grid lines. The number of crossings is the approximate length of the curve in millimetres. The design of the Steinhaus longimeter can be seen as an application of the Crofton formula, according to which the length of a curve equals the expected number of times it is crossed by a random line. See also * Opisometer, a mechanical device for measuring curve length by rolling a small wheel along the curve * Dot planimeter, a similar transparency-based device for estimating area, based on Pick's theorem References Bibliography * Hugo Steinhaus: Zur Praxis der Rectification und zum Längenbegriff, ''Berichte der Sächsis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radon Transform
In mathematics, the Radon transform is the integral transform which takes a function ''f'' defined on the plane to a function ''Rf'' defined on the (two-dimensional) space of lines in the plane, whose value at a particular line is equal to the line integral of the function over that line. The transform was introduced in 1917 by Johann Radon, who also provided a formula for the inverse transform. Radon further included formulas for the transform in three dimensions, in which the integral is taken over planes (integrating over lines is known as the X-ray transform). It was later generalized to higher-dimensional Euclidean spaces, and more broadly in the context of integral geometry. The complex analogue of the Radon transform is known as the Penrose transform. The Radon transform is widely applicable to tomography, the creation of an image from the projection data associated with cross-sectional scans of an object. Explanation If a function f represents an unknown density, the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Buffon's Noodle
In geometric probability, the problem of Buffon's noodle is a variation on the well-known problem of Buffon's needle, named after Georges-Louis Leclerc, Comte de Buffon who lived in the 18th century. This approach to the problem was published by Joseph-Émile Barbier in 1860. Buffon's needle Suppose there exist infinitely many equally spaced parallel lines, and we were to randomly toss a needle whose length is less than or equal to the distance between adjacent lines. What is the probability that the needle will lie across a line upon landing? To solve this problem, let \ell be the length of the needle and D be the distance between two adjacent lines. Then, let \theta be the acute angle the needle makes with the horizontal, and let x be the distance from the center of the needle to the nearest line. The needle lies across the nearest line if and only if x \le \frac . We see this condition from the right triangle formed by the needle, the nearest line, and the line of l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Body Of Constant Brightness
In convex geometry, a body of constant brightness is a three-dimensional convex set all of whose two-dimensional projections have equal area. A sphere is a body of constant brightness, but others exist. Bodies of constant brightness are a generalization of curves of constant width, but are not the same as another generalization, the surfaces of constant width. The name comes from interpreting the body as a shining body with isotropic luminance, then a photo (with focus at infinity) of the body taken from any angle would have the same total light energy hitting the photo. Properties A body has constant brightness if and only if the reciprocal Gaussian curvatures at pairs of opposite points of tangency of parallel supporting planes have almost-everywhere-equal sums. According to an analogue of Barbier's theorem, all bodies of constant brightness that have the same projected area A as each other also have the same surface area, \textstyle\sqrt. This can be proved by the Crofton ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Hull
In geometry, the convex hull or convex envelope or convex closure of a shape is the smallest convex set that contains it. The convex hull may be defined either as the intersection of all convex sets containing a given subset of a Euclidean space, or equivalently as the set of all convex combinations of points in the subset. For a bounded subset of the plane, the convex hull may be visualized as the shape enclosed by a rubber band stretched around the subset. Convex hulls of open sets are open, and convex hulls of compact sets are compact. Every compact convex set is the convex hull of its extreme points. The convex hull operator is an example of a closure operator, and every antimatroid can be represented by applying this closure operator to finite sets of points. The algorithmic problems of finding the convex hull of a finite set of points in the plane or other low-dimensional Euclidean spaces, and its dual problem of intersecting half-spaces, are fundamental problems of co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Curve Of Constant Width
In geometry, a curve of constant width is a simple closed curve in the plane whose width (the distance between parallel supporting lines) is the same in all directions. The shape bounded by a curve of constant width is a body of constant width or an orbiform, the name given to these shapes by Leonhard Euler. Standard examples are the circle and the Reuleaux triangle. These curves can also be constructed using circular arcs centered at crossings of an arrangement of lines, as the involutes of certain curves, or by intersecting circles centered on a partial curve. Every body of constant width is a convex set, its boundary crossed at most twice by any line, and if the line crosses perpendicularly it does so at both crossings, separated by the width. By Barbier's theorem, the body's perimeter is exactly times its width, but its area depends on its shape, with the Reuleaux triangle having the smallest possible area for its width and the circle the largest. Every superset of a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Barbier's Theorem
In geometry, Barbier's theorem states that every curve of constant width has perimeter times its width, regardless of its precise shape. This theorem was first published by Joseph-Émile Barbier in 1860. Examples The most familiar examples of curves of constant width are the circle and the Reuleaux triangle. For a circle, the width is the same as the diameter; a circle of width ''w'' has perimeter ''w''. A Reuleaux triangle of width ''w'' consists of three arcs of circles of radius ''w''. Each of these arcs has central angle /3, so the perimeter of the Reuleaux triangle of width ''w'' is equal to half the perimeter of a circle of radius ''w'' and therefore is equal to ''w''. A similar analysis of other simple examples such as Reuleaux polygons gives the same answer. Proofs One proof of the theorem uses the properties of Minkowski sums. If ''K'' is a body of constant width ''w'', then the Minkowski sum of ''K'' and its 180° rotation is a disk with radius ''w'' and pe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isoperimetric Inequality
In mathematics, the isoperimetric inequality is a geometric inequality involving the perimeter of a set and its volume. In n-dimensional space \R^n the inequality lower bounds the surface area or perimeter \operatorname(S) of a set S\subset\R^n by its volume \operatorname(S), :\operatorname(S)\geq n \operatorname(S)^ \, \operatorname(B_1)^, where B_1\subset\R^n is a unit sphere. The equality holds only when S is a sphere in \R^n. On a plane, i.e. when n=2, the isoperimetric inequality relates the square of the circumference of a closed curve and the area of a plane region it encloses. '' Isoperimetric'' literally means "having the same perimeter". Specifically in \R ^2, the isoperimetric inequality states, for the length ''L'' of a closed curve and the area ''A'' of the planar region that it encloses, that : L^2 \ge 4\pi A, and that equality holds if and only if the curve is a circle. The isoperimetric problem is to determine a plane figure of the largest possible area whose ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bounding Volume Hierarchy
A bounding volume hierarchy (BVH) is a tree structure on a set of geometric objects. All geometric objects, that form the leaf nodes of the tree, are wrapped in bounding volumes. These nodes are then grouped as small sets and enclosed within larger bounding volumes. These, in turn, are also grouped and enclosed within other larger bounding volumes in a recursive fashion, eventually resulting in a tree structure with a single bounding volume at the top of the tree. Bounding volume hierarchies are used to support several operations on sets of geometric objects efficiently, such as in collision detection and ray tracing (graphics), ray tracing. Although wrapping objects in bounding volumes and performing collision tests on them before testing the object geometry itself simplifies the tests and can result in significant performance improvements, the same number of pairwise tests between bounding volumes are still being performed. By arranging the bounding volumes into a bounding volum ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |