|
Crisis (dynamical Systems)
In applied mathematics and astrodynamics, in the theory of dynamical systems, a crisis is the sudden appearance or disappearance of a strange attractor as the parameters of a dynamical system are varied. This global bifurcation occurs when a chaotic attractor comes into contact with an unstable periodic orbit or its stable manifold. As the orbit approaches the unstable orbit it will diverge away from the previous attractor, leading to a qualitatively different behaviour. Crises can produce intermittent behaviour. Grebogi, Ott, Romeiras, and Yorke distinguished between three types of crises: * The first type, a boundary or an exterior crisis, the attractor is suddenly destroyed as the parameters are varied. In the postbifurcation state the motion is transiently chaotic, moving chaotically along the former attractor before being attracted to a fixed point, periodic orbit, quasiperiodic orbit, another strange attractor, or diverging to infinity. * In the second type of crisis, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
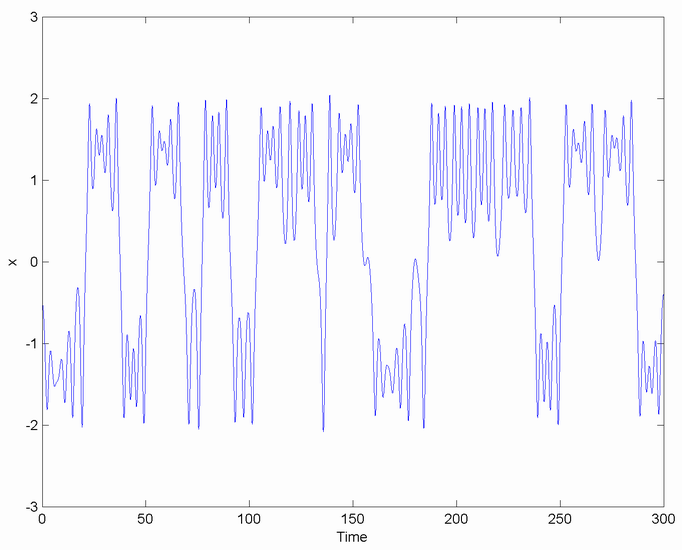
Bifurcations And Crises Of Ikeda Attractor
Bifurcation or bifurcated may refer to: Science and technology * Bifurcation theory, the study of sudden changes in dynamical systems ** Bifurcation, of an incompressible flow, modeled by squeeze mapping the fluid flow * River bifurcation, the forking of a river into its tributaries * Bifurcation lake, a lake that flows into two different drainage basins * Bifurcated bonding, a single hydrogen atom participates in two hydrogen bonds Other uses * Bifurcation (law), the division of issues in a trial See also * Aortic bifurcation, the point at which the abdominal aorta bifurcates into the left and right common iliac arteries * Tracheal bifurcation, or the carina of trachea (Latin: ''bifurcatio tracheae'') * Bifurcation diagram * Bifurcate merging, a kinship system * False dilemma or bifurcation * Tongue bifurcation (other) * Fork (other) A fork is a utensil for eating and cooking. Fork may also refer to: Implements * Fork (road), a type of intersection where a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Intermittency
In dynamical systems, intermittency is the irregular alternation of phases of apparently periodic and chaotic dynamics ( Pomeau–Manneville dynamics), or different forms of chaotic dynamics (crisis-induced intermittency). Pomeau and Manneville described three routes to intermittency where a nearly periodic system shows irregularly spaced bursts of chaos. These (type I, II and III) correspond to the approach to a saddle-node bifurcation, a subcritical Hopf bifurcation, or an inverse period-doubling bifurcation. In the apparently periodic phases the behaviour is only nearly periodic, slowly drifting away from an unstable periodic orbit. Eventually the system gets far enough away from the periodic orbit to be affected by chaotic dynamics in the rest of the state space, until it gets close to the orbit again and returns to the nearly periodic behaviour. Since the time spent near the periodic orbit depends sensitively on how closely the system entered its vicinity (in turn dete ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dynamical Systems
In mathematics, a dynamical system is a system in which a function describes the time dependence of a point in an ambient space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, the random motion of particles in the air, and the number of fish each springtime in a lake. The most general definition unifies several concepts in mathematics such as ordinary differential equations and ergodic theory by allowing different choices of the space and how time is measured. Time can be measured by integers, by real or complex numbers or can be a more general algebraic object, losing the memory of its physical origin, and the space may be a manifold or simply a set, without the need of a smooth space-time structure defined on it. At any given time, a dynamical system has a state representing a point in an appropriate state space. This state is often given by a tuple of real numbers or by a vector in a geometrical manif ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phase Portrait
A phase portrait is a geometric representation of the trajectories of a dynamical system in the phase plane. Each set of initial conditions is represented by a different curve, or point. Phase portraits are an invaluable tool in studying dynamical systems. They consist of a plot of typical trajectories in the state space. This reveals information such as whether an attractor, a repellor or limit cycle is present for the chosen parameter value. The concept of topological equivalence is important in classifying the behaviour of systems by specifying when two different phase portraits represent the same qualitative dynamic behavior. An attractor is a stable point which is also called "sink". The repeller is considered as an unstable point, which is also known as "source". A phase portrait graph of a dynamical system depicts the system's trajectories (with arrows) and stable steady states (with dots) and unstable steady states (with circles) in a state space. The axes are of st ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bifurcation Diagram
In mathematics, particularly in dynamical systems, a bifurcation diagram shows the values visited or approached asymptotically (fixed points, periodic orbits, or chaotic attractors) of a system as a function of a bifurcation parameter in the system. It is usual to represent stable values with a solid line and unstable values with a dotted line, although often the unstable points are omitted. Bifurcation diagrams enable the visualization of bifurcation theory. Logistic map An example is the bifurcation diagram of the logistic map: : x_=rx_n(1-x_n). \, The bifurcation parameter ''r'' is shown on the horizontal axis of the plot and the vertical axis shows the set of values of the logistic function visited asymptotically from almost all initial conditions. The bifurcation diagram shows the forking of the periods of stable orbits from 1 to 2 to 4 to 8 etc. Each of these bifurcation points is a period-doubling bifurcation. The ratio of the lengths of successive intervals between ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Intermittency
In dynamical systems, intermittency is the irregular alternation of phases of apparently periodic and chaotic dynamics ( Pomeau–Manneville dynamics), or different forms of chaotic dynamics (crisis-induced intermittency). Pomeau and Manneville described three routes to intermittency where a nearly periodic system shows irregularly spaced bursts of chaos. These (type I, II and III) correspond to the approach to a saddle-node bifurcation, a subcritical Hopf bifurcation, or an inverse period-doubling bifurcation. In the apparently periodic phases the behaviour is only nearly periodic, slowly drifting away from an unstable periodic orbit. Eventually the system gets far enough away from the periodic orbit to be affected by chaotic dynamics in the rest of the state space, until it gets close to the orbit again and returns to the nearly periodic behaviour. Since the time spent near the periodic orbit depends sensitively on how closely the system entered its vicinity (in turn dete ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Basin Of Attraction
In the mathematical field of dynamical systems, an attractor is a set of states toward which a system tends to evolve, for a wide variety of starting conditions of the system. System values that get close enough to the attractor values remain close even if slightly disturbed. In finite-dimensional systems, the evolving variable may be represented algebraically as an ''n''-dimensional vector. The attractor is a region in ''n''-dimensional space. In physical systems, the ''n'' dimensions may be, for example, two or three positional coordinates for each of one or more physical entities; in economic systems, they may be separate variables such as the inflation rate and the unemployment rate. If the evolving variable is two- or three-dimensional, the attractor of the dynamic process can be represented geometrically in two or three dimensions, (as for example in the three-dimensional case depicted to the right). An attractor can be a point, a finite set of points, a curve, a manif ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quasiperiodic Motion
In mathematics and theoretical physics, quasiperiodic motion is in rough terms the type of motion executed by a dynamical system containing a finite number (two or more) of incommensurable frequencies. That is, if we imagine that the phase space is modelled by a torus ''T'' (that is, the variables are periodic like angles), the trajectory of the system is modelled by a curve on ''T'' that wraps around the torus without ever exactly coming back on itself. A quasiperiodic function on the real line is the type of function (continuous, say) obtained from a function on ''T'', by means of a curve :''R'' → ''T'' which is linear (when lifted from ''T'' to its covering Euclidean space), by composition. It is therefore oscillating, with a finite number of underlying frequencies. (NB the sense in which theta functions and the Weierstrass zeta function in complex analysis are said to have quasi-periods with respect to a period lattice is something distinct from this.) The theory of alm ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fixed Point (mathematics)
A fixed point (sometimes shortened to fixpoint, also known as an invariant point) is a value that does not change under a given transformation. Specifically, in mathematics, a fixed point of a function is an element that is mapped to itself by the function. In physics, the term fixed point can refer to a temperature that can be used as a reproducible reference point, usually defined by a phase change or triple point. Fixed point of a function Formally, is a fixed point of a function if belongs to both the domain and the codomain of , and . For example, if is defined on the real numbers by f(x) = x^2 - 3 x + 4, then 2 is a fixed point of , because . Not all functions have fixed points: for example, , has no fixed points, since is never equal to for any real number. In graphical terms, a fixed point means the point is on the line , or in other words the graph of has a point in common with that line. Fixed-point iteration In numerical analysis, ''fixed-point iter ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stable Manifold
In mathematics, and in particular the study of dynamical systems, the idea of ''stable and unstable sets'' or stable and unstable manifolds give a formal mathematical definition to the general notions embodied in the idea of an attractor or repellor. In the case of hyperbolic dynamics, the corresponding notion is that of the hyperbolic set. Physical example The gravitational tidal forces acting on the rings of Saturn provide an easy-to-visualize physical example. The tidal forces flatten the ring into the equatorial plane, even as they stretch it out in the radial direction. Imagining the rings to be sand or gravel particles ("dust") in orbit around Saturn, the tidal forces are such that any perturbations that push particles above or below the equatorial plane results in that particle feeling a restoring force, pushing it back into the plane. Particles effectively oscillate in a harmonic well, damped by collisions. The stable direction is perpendicular to the ring. The unstable di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Applied Mathematics
Applied mathematics is the application of mathematical methods by different fields such as physics, engineering, medicine, biology, finance, business, computer science, and industry. Thus, applied mathematics is a combination of mathematical science and specialized knowledge. The term "applied mathematics" also describes the professional specialty in which mathematicians work on practical problems by formulating and studying mathematical models. In the past, practical applications have motivated the development of mathematical theories, which then became the subject of study in pure mathematics where abstract concepts are studied for their own sake. The activity of applied mathematics is thus intimately connected with research in pure mathematics. History Historically, applied mathematics consisted principally of applied analysis, most notably differential equations; approximation theory (broadly construed, to include representations, asymptotic methods, variational ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Periodic Orbit
In mathematics, in the study of iterated functions and dynamical systems, a periodic point of a function is a point which the system returns to after a certain number of function iterations or a certain amount of time. Iterated functions Given a mapping ''f'' from a set ''X'' into itself, :f: X \to X, a point ''x'' in ''X'' is called periodic point if there exists an ''n'' so that :\ f_n(x) = x where f_n is the ''n''th iterate of ''f''. The smallest positive integer ''n'' satisfying the above is called the ''prime period'' or ''least period'' of the point ''x''. If every point in ''X'' is a periodic point with the same period ''n'', then ''f'' is called ''periodic'' with period ''n'' (this is not to be confused with the notion of a periodic function). If there exist distinct ''n'' and ''m'' such that :f_n(x) = f_m(x) then ''x'' is called a preperiodic point. All periodic points are preperiodic. If ''f'' is a diffeomorphism of a differentiable manifold, so that the derivative f_n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |