|
Cone Lumber Company
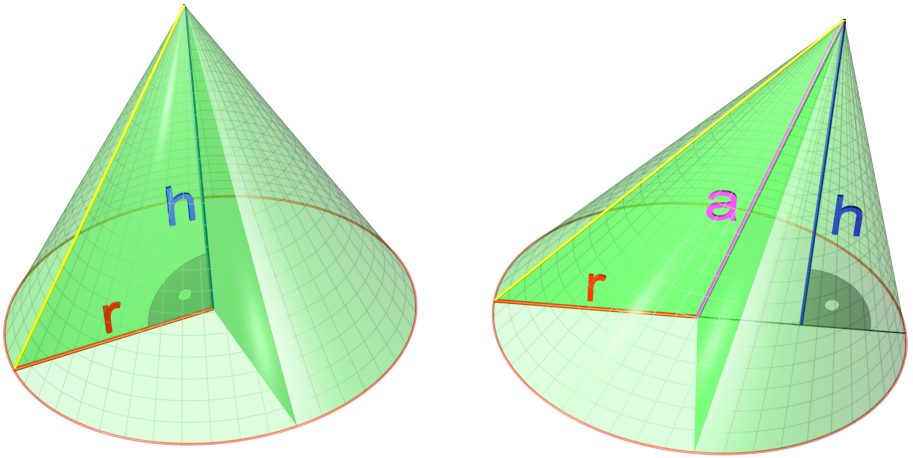
A cone is a three-dimensional geometric shape that tapers smoothly from a flat base (frequently, though not necessarily, circular) to a point called the apex or vertex. A cone is formed by a set of line segments, half-lines, or lines connecting a common point, the apex, to all of the points on a base that is in a plane that does not contain the apex. Depending on the author, the base may be restricted to be a circle, any one-dimensional quadratic form in the plane, any closed one-dimensional figure, or any of the above plus all the enclosed points. If the enclosed points are included in the base, the cone is a solid object; otherwise it is a two-dimensional object in three-dimensional space. In the case of a solid object, the boundary formed by these lines or partial lines is called the ''lateral surface''; if the lateral surface is unbounded, it is a conical surface. In the case of line segments, the cone does not extend beyond the base, while in the case of half- ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cone 3d
A cone is a three-dimensional space, three-dimensional geometric shape that tapers smoothly from a flat base (frequently, though not necessarily, circular) to a point called the Apex (geometry), apex or vertex (geometry), vertex. A cone is formed by a set of line segments, half-lines, or line (geometry), lines connecting a common point, the apex, to all of the points on a base that is in a plane (geometry), plane that does not contain the apex. Depending on the author, the base may be restricted to be a circle, any one-dimensional quadratic form in the plane, any closed one-dimensional space, one-dimensional figure, or any of the above plus all the enclosed points. If the enclosed points are included in the base, the cone is a solid geometry, solid object; otherwise it is a two-dimensional object in three-dimensional space. In the case of a solid object, the boundary formed by these lines or partial lines is called the ''lateral surface''; if the lateral surface is unbounded ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rotational Symmetry
Rotational symmetry, also known as radial symmetry in geometry, is the property a shape has when it looks the same after some rotation by a partial turn. An object's degree of rotational symmetry is the number of distinct orientations in which it looks exactly the same for each rotation. Certain geometric objects are partially symmetrical when rotated at certain angles such as squares rotated 90°, however the only geometric objects that are fully rotationally symmetric at any angle are spheres, circles and other spheroids. Formal treatment Formally the rotational symmetry is symmetry with respect to some or all rotations in ''m''-dimensional Euclidean space. Rotations are direct isometries, i.e., isometries preserving orientation. Therefore, a symmetry group of rotational symmetry is a subgroup of ''E''+(''m'') (see Euclidean group). Symmetry with respect to all rotations about all points implies translational symmetry with respect to all translations, so space is homo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dandelin Spheres
In geometry, the Dandelin spheres are one or two spheres that are tangent both to a plane and to a cone that intersects the plane. The intersection of the cone and the plane is a conic section, and the point at which either sphere touches the plane is a focus of the conic section, so the Dandelin spheres are also sometimes called focal spheres.Taylor, Charles. ''An Introduction to the Ancient and Modern Geometry of Conics''page 196 ("focal spheres") (Deighton, Bell and co., 1881). The Dandelin spheres were discovered in 1822. They are named in honor of the French mathematician |
Directrix (conic Section)
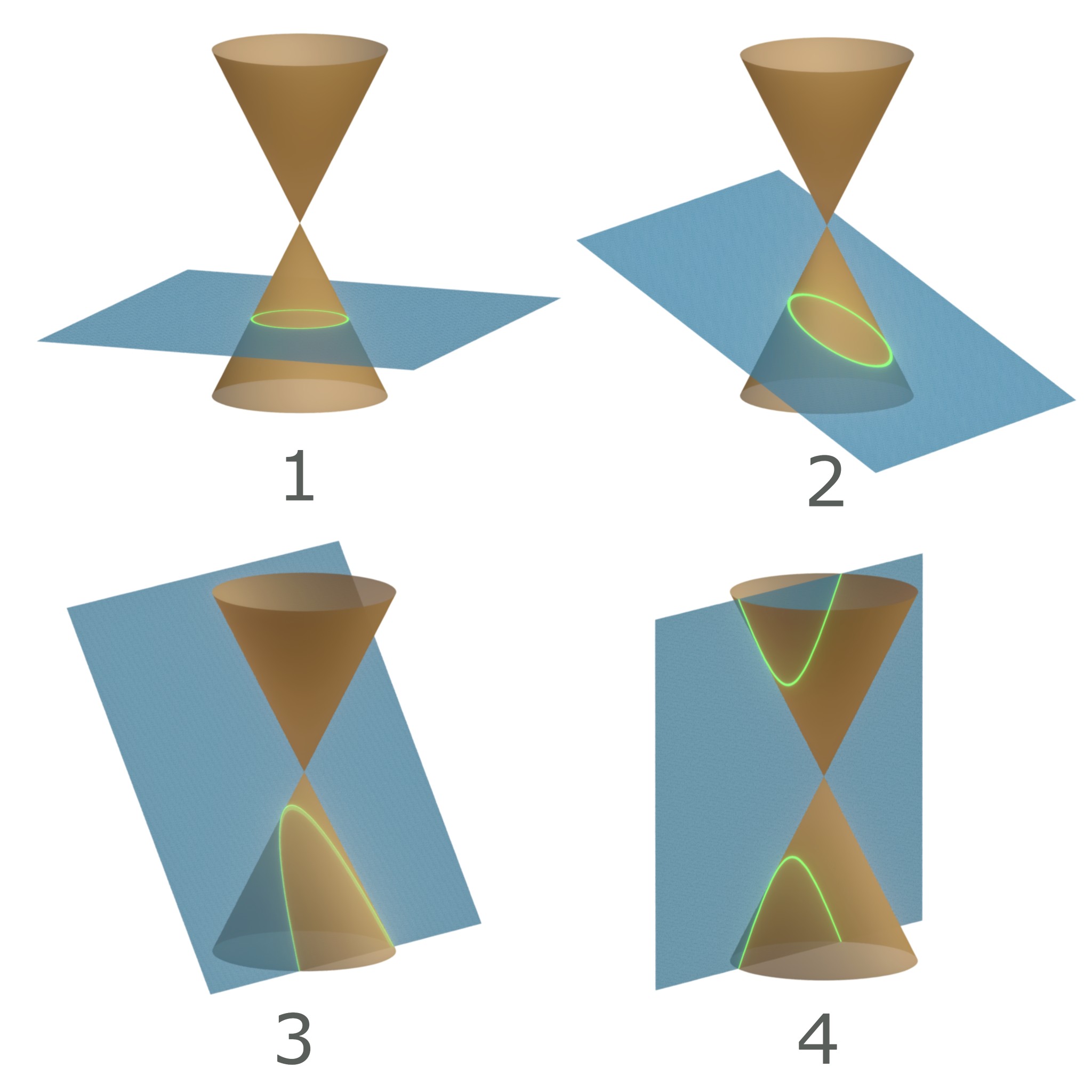
In mathematics, a conic section, quadratic curve or conic is a curve obtained as the intersection of the surface of a cone with a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, though historically it was sometimes called a fourth type. The ancient Greek mathematicians studied conic sections, culminating around 200 BC with Apollonius of Perga's systematic work on their properties. The conic sections in the Euclidean plane have various distinguishing properties, many of which can be used as alternative definitions. One such property defines a non-circular conic to be the set of those points whose distances to some particular point, called a ''focus'', and some particular line, called a ''directrix'', are in a fixed ratio, called the ''eccentricity''. The type of conic is determined by the value of the eccentricity. In analytic geometry, a conic may be defined as a plane algebraic curve of deg ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dimension
In physics and mathematics, the dimension of a Space (mathematics), mathematical space (or object) is informally defined as the minimum number of coordinates needed to specify any Point (geometry), point within it. Thus, a Line (geometry), line has a dimension of one (1D) because only one coordinate is needed to specify a point on itfor example, the point at 5 on a number line. A Surface (mathematics), surface, such as the Boundary (mathematics), boundary of a Cylinder (geometry), cylinder or sphere, has a dimension of two (2D) because two coordinates are needed to specify a point on itfor example, both a latitude and longitude are required to locate a point on the surface of a sphere. A two-dimensional Euclidean space is a two-dimensional space on the Euclidean plane, plane. The inside of a cube, a cylinder or a sphere is three-dimensional (3D) because three coordinates are needed to locate a point within these spaces. In classical mechanics, space and time are different categ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Projective Cone
A projective cone (or just cone) in projective geometry is the union of all lines that intersect a projective subspace ''R'' (the apex of the cone) and an arbitrary subset ''A'' (the basis) of some other subspace ''S'', disjoint from ''R''. In the special case that ''R'' is a single point, ''S'' is a plane, and ''A'' is a conic section on ''S'', the projective cone is a conical surface; hence the name. Definition Let ''X'' be a projective space over some field ''K'', and ''R'', ''S'' be disjoint subspaces of ''X''. Let ''A'' be an arbitrary subset of ''S''. Then we define ''RA'', the cone with top ''R'' and basis ''A'', as follows : * When ''A'' is empty, ''RA'' = ''A''. * When ''A'' is not empty, ''RA'' consists of all those points on a line connecting a point on ''R'' and a point on ''A''. Properties * As ''R'' and ''S'' are disjoint, one may deduce from linear algebra and the definition of a projective space that every point on ''RA'' not in ''R'' or ''A'' is on exactly ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Cone
In linear algebra, a ''cone''—sometimes called a linear cone for distinguishing it from other sorts of cones—is a subset of a vector space that is closed under scalar multiplication; that is, is a cone if x\in C implies sx\in C for every . When the scalars are real numbers, or belong to an ordered field, one generally calls a cone a subset of a vector space that is closed under multiplication by a ''positive scalar''. In this context, a convex cone is a cone that is closed under addition, or, equivalently, a subset of a vector space that is closed under linear combinations with positive coefficients. It follows that convex cones are convex sets. In this article, only the case of scalars in an ordered field is considered. Definition A subset ''C'' of a vector space ''V'' over an ordered field ''F'' is a cone (or sometimes called a linear cone) if for each ''x'' in ''C'' and positive scalar ''α'' in ''F'', the product ''αx'' is in ''C''. Note that some authors define co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pyramid (geometry)
In geometry, a pyramid () is a polyhedron formed by connecting a polygonal base and a point, called the apex. Each base edge and apex form a triangle, called a ''lateral face''. It is a conic solid with polygonal base. A pyramid with an base has vertices, faces, and edges. All pyramids are self-dual. A right pyramid has its apex directly above the centroid of its base. Nonright pyramids are called oblique pyramids. A regular pyramid has a regular polygon base and is usually implied to be a ''right pyramid''. When unspecified, a pyramid is usually assumed to be a ''regular'' square pyramid, like the physical pyramid structures. A triangle-based pyramid is more often called a tetrahedron. Among oblique pyramids, like acute and obtuse triangles, a pyramid can be called ''acute'' if its apex is above the interior of the base and ''obtuse'' if its apex is above the exterior of the base. A right-angled pyramid has its apex above an edge or vertex of the base. In a tetrahedro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polygon
In geometry, a polygon () is a plane figure that is described by a finite number of straight line segments connected to form a closed ''polygonal chain'' (or ''polygonal circuit''). The bounded plane region, the bounding circuit, or the two together, may be called a polygon. The segments of a polygonal circuit are called its '' edges'' or ''sides''. The points where two edges meet are the polygon's '' vertices'' (singular: vertex) or ''corners''. The interior of a solid polygon is sometimes called its ''body''. An ''n''-gon is a polygon with ''n'' sides; for example, a triangle is a 3-gon. A simple polygon is one which does not intersect itself. Mathematicians are often concerned only with the bounding polygonal chains of simple polygons and they often define a polygon accordingly. A polygonal boundary may be allowed to cross over itself, creating star polygons and other self-intersecting polygons. A polygon is a 2-dimensional example of the more general polytope in any number ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Area (geometry)
Area is the quantity that expresses the extent of a region on the plane or on a curved surface. The area of a plane region or ''plane area'' refers to the area of a shape or planar lamina, while '' surface area'' refers to the area of an open surface or the boundary of a three-dimensional object. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat. It is the two-dimensional analogue of the length of a curve (a one-dimensional concept) or the volume of a solid (a three-dimensional concept). The area of a shape can be measured by comparing the shape to squares of a fixed size. In the International System of Units (SI), the standard unit of area is the square metre (written as m2), which is the area of a square whose sides are one metre long. A shape with an area of three square metres would have the same area as three such squares. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Polytopes
''Convex Polytopes'' is a graduate-level mathematics textbook about convex polytopes, higher-dimensional generalizations of three-dimensional convex polyhedra. It was written by Branko Grünbaum, with contributions from Victor Klee, Micha Perles, and G. C. Shephard, and published in 1967 by John Wiley & Sons. It went out of print in 1970. A second edition, prepared with the assistance of Volker Kaibel, Victor Klee, and Günter M. Ziegler, was published by Springer-Verlag in 2003, as volume 221 of their book series Graduate Texts in Mathematics. ''Convex Polytopes'' was the winner of the 2005 Leroy P. Steele Prize for mathematical exposition, given by the American Mathematical Society. The Basic Library List Committee of the Mathematical Association of America has recommended its inclusion in undergraduate mathematics libraries. Topics The book has 19 chapters. After two chapters introducing background material in linear algebra, topology, and convex geometry, two more chapters ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conic Section
In mathematics, a conic section, quadratic curve or conic is a curve obtained as the intersection of the surface of a cone with a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, though historically it was sometimes called a fourth type. The ancient Greek mathematicians studied conic sections, culminating around 200 BC with Apollonius of Perga's systematic work on their properties. The conic sections in the Euclidean plane have various distinguishing properties, many of which can be used as alternative definitions. One such property defines a non-circular conic to be the set of those points whose distances to some particular point, called a ''focus'', and some particular line, called a ''directrix'', are in a fixed ratio, called the ''eccentricity''. The type of conic is determined by the value of the eccentricity. In analytic geometry, a conic may be defined as a plane algebraic curve of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |